How to traverse in a tree?

Suppose you’re given an array filled with N elements. How will you traverse all N elements?

Why is this even a question, right? You will go from index 0 to index N-1 and thereby, traverse all elements of the array.

But what if you’re given the root of a tree? Can you traverse that tree? How will you traverse all elements of that tree?

Introduction to Tree Traversals

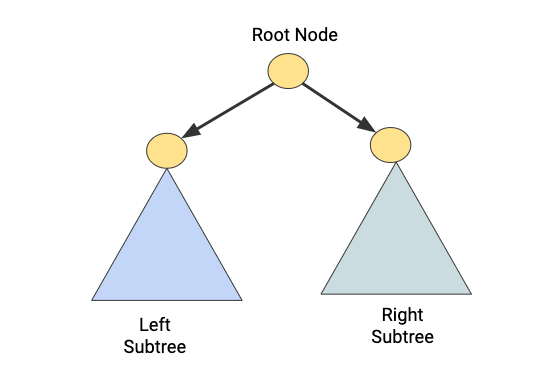
There is a clear recursive structure in a tree data structure where we can solve a problem using the solution of its smaller subproblems. So we need to access three different elements in the tree:

Root Node
Nodes in the left subtree
Nodes in the right sub-tree

We can access these three elements in six different ways i.e. there are 6 possible permutations. These are also called DFS traversal of a tree:

Pre-order: Root -> Left subtree -> Right subtree
Reverse Pre-order: Root -> Right subtree -> Left subtree
In-order: Left subtree -> Root -> Right subtree
Reverse In-order: Right subtree -> Root -> Left subtree
Post-Order: Left subtree -> Right subtree -> Root
Reverse Post-order: Right subtree -> Left subtree -> Root

There are some other types of Non-Recursive traversals in trees that you can practice. We can use these traversals in the solution of several tree problems:

BFS Traversal or Level order traversal (Using Queue)
Iterative Traversals (Using Stack): Pre-order, In-order and Post-order
Morris Traversal or Threaded Binary tree Traversal

Can you think of some other ways of traversing elements in a tree?

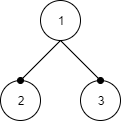
In this blog, we are going to discuss the recursive and Iterative approach of following three traversals:

Preorder(NLR): Traverse the node, then the left child(L) and then the right child(R) → 1 2 3 ( The preorder traversal of above tree )
Inorder(LNR): Traverse the left child(L), the node(N) and then the right child(R) → 2 1 3
Postorder(LRN): Traverse the left child(L), the right child(R) and then the node(N) → 2 3 1

1. Preorder Traversal

Preorder Traversal as we read above, traverse the tree in the order: Node, left child and then the right child.

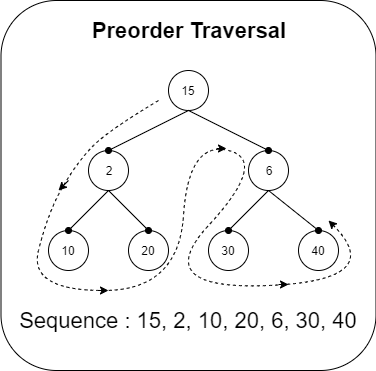
Recursive Implementation

Tree traversals are naturally recursive in nature so let’s see its recursive implementation first →

void printPreorder(TreeNode root)
{
    if ( root == NULL )
        return 
    
    print ( root.val )
    printPreorder( root.left )
    printPreorder( root.right )
}

Simple to understand, right?

Well, let’s dive deeper now. In the recursion, the compiler does the stack maintenance for us. Let us try do it ourselves now.

Iterative implementation

Now we need to implement the stack ourselves. We need to perform the push() and pop() operations.

Solution Steps →

Create a stack preorder that will temporarily store the elements like the function stack in the above recursion.
Since priority is given to the root, push the root first to the stack.
Now we will run a loop until the stack empties, i.e., there are no more elements left to process.

Now, what order did we follow in the above recursion? Print node, Recurse left and then recurse right . We shall follow the same order in iteration too.

4. In each iteration, print the node (i.e. the element at top of the stack) then push the right child in the stack and then the left child.

★ Why did we push the right child first? So that the left child gets to be on top and is processed first.

5. Don’t forget to pop the top node after printing it in each iteration.

Pseudo Code

void printPreorder(TreeNode root)
{
    Create stack 'preorder' to fit elements of type TreeNode 
    preorder.push( root )
    while ( preorder.empty() != True )
    {
        TreeNode node = preorder.peek()
        preorder.pop()
        if ( node == NULL )
            continue
        
        print ( node.val )
        // Note that right child is pushed first
        // so that left child is on top
        preorder.push( node.right )
        preorder.push( node.left )
    } 
}

Inorder Traversal

Inorder Traversal follows the order LNR (left, node, right).

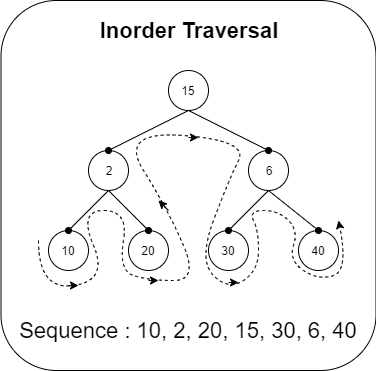
Recursive Implementation

void printInorder(TreeNode root)
{
    if ( root == NULL )
        return
    
    printInorder( root.left )
    print ( root.val )
    printInorder( root.right )
}

Can you implement this iteratively now using stacks? Let’s try.

Iterative Implementation

Let’s form a strategy to approach the problem. Okay so first of all, we need to find the left-most node of our current tree. The leftmost node gets printed first. But what next? We now need the parent node and then the right sibling of this node. So we shall proceed in that manner and continue doing so until our stack is empty.

Solution Steps →

Create a stack inorder to fit elements of type TreeNode
Run a while loop until there are no more elements to process, i.e. the root is NULL and the stack is empty
In each iteration →

Keep moving to the left child until it exists and push the elements onto the stack so that we can process them after we process the leftmost element
Once we reach the left-most element of current subtree, print it and remove it from the stack.
What’s the next priority? Either the right subtree or current node or its parent.
So we move to its right child if it exists. If it doesn’t the parent node is already in the stack. Pop it and process it

4. Repeat the process until all elements are processed

Pseudo Code

void printInorder(TreeNode root)
{
    Create stack 'inorder' to fit elements of type TreeNode
    while ( root != NULL or inorder.empty() != True )
    {
        // Find the leftmost node
        while( root != NULL )
        {
            inorder.push(root)
            root = root.left
        }
        
        root = inorder.peek()
        inorder.pop()
        print( root )
        root = root.right
    }
}

Postorder Traversal

Postorder Traversal follows the LRN policy (left, right, node)

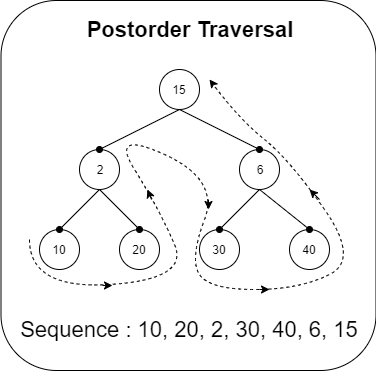
Recursive Implementation

void printPostorder(TreeNode root)
{
    if ( root == NULL )
        return

    printPostorder(root.left)
    printPostorder(root.right)
    print ( root.val )
}

What about the iterative implementation? Can you try it yourself based on what you learnt in the above two iterative implementations?

Iterative Implementation

Let’s go through it in an organized manner. Let us assume we have a stack that prints postorder traversal of the tree when its elements are popped.

→ Which element do you suppose should be at the bottom-most position of such a stack? the root of tree ( node is given the least preference)

→ And which element should be at the top-most position of this stack? the leftmost element in the tree( left child is given the highest priority)

So in order to create this stack, we should first push the root, then the right subtree and then the left subtree so that the left subtree is at the top of the stack. Same priority must be extended while pushing the individual subtrees.

Okay so now let’s design the solution steps keeping in mind the above priorities.

Solution Steps →

Firstly, create a stack st which we will use for storing elements temporarily and then create another stack postorder which will store elements as mentioned above.
Push the root in st.
Run a loop until st is not empty, i.e. until all elements haven’t been processed. In each iteration,

Pop the top element of st and push it to postorder . This element is the root of the current subtree and has lowest priority in postorder and is therefore pushed first onto the stack.
As mentioned above, we need the left subtree above right subtree in the postorder stack, therefore, we first push the left child of the current node and then the right child so that the right child is on top and pushed onto postorder stack first.

4. Now the postorder stack is created!

5. Pop and print the top element of the postorder stack.

6. Keep repeating step 5 until the postorder stack is empty.

Pseudo Code

void printPostorder(TreeNode root)
{
    Create stack 'st' and 'postorder' to fit TreeNode elements
    st.push(root)
    while ( st.empty() != True )
    {
        root = st.peek()
        st.pop()
        if( root == NULL )
            continue
        postorder.push(root)
        st.push(root.left)
        st.push(root.right)
    }
    while( postorder.empty() != True )
    {
        TreeNode temp = postorder.peek()
        print ( temp.val )
        postorder.pop()
    }
}

Critical ideas to explore further

Identify some problems where we use the above traversals for the solution.
Why we use queue data structure in the BFS traversal or level order traversal?
Visualize and practice iterative traversals using stack.
Tree is a special type of graph! Understand the properties of tree in terms of graph data structure.

Happy Coding! Enjoy Algorithms!