Triplet With Zero Sum

Difficulty Medium

Companies: Facebook, Amazon, Microsoft

Problem Description: Given an array arr[ ] of n integers, are there elements x, y, z in arr such that x + y + z = 0? Find all unique triplets in the array which gives the sum of zero.

Problem Note

• The solution set must not contain duplicate triplets.
• Triplet must be in ascending order. (i.e. a ≤ b ≤ c)

Example 1

Input: A[]= [-1, 0, 1, 2, -1, -4]
Output: [[-1, 0, 1],[-1, -1, 2]]

Example 2

Input: A[] = [1, -2, 1, 0, 5]
Output: [[-2, 1, 1]]

You may try to solve this problem here first.

Solutions

We will be discussing three different approaches to solve this problem

1. Brute Force approach
2. Using Hash Set
3. Using a two-pointer approach

1. Brute Force Approach

The naive approach is that we could create three nested loops and check one by one that the sum of all the three elements is zero or not. If the sum of the three elements is zero then print elements.

Solution Step

• Use three loops and check one by one that the sum of the three elements is equal to zero or not.
• If the sum of 3 elements is equal to zero, then print elements.

Pseudo Code

int[][] find_triplets(int arr[], int n){
    res[]
    sort(arr)
    for (int i = 0; i < n – 2; i++) {
        for (int j = i + 1; j < n – 1; j++) {
            for (int k = j + 1; k < n; k++) {
                if (arr[i] + arr[j] + arr[k] == 0) {
                    res.add([arr[i], arr[j], arr[k]])
                }
            }
        }
    }
}

Complexity Analysis

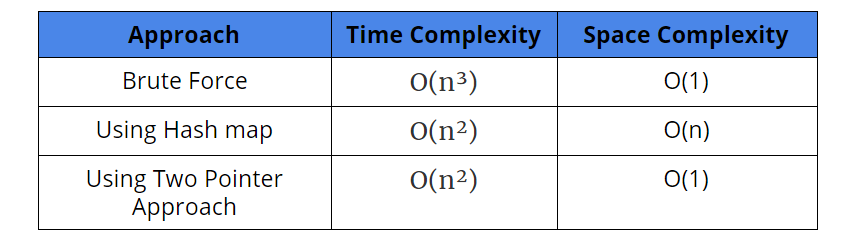
Time Complexity: O(n³)

Space Complexity: O(1)

Critical Ideas to Think

• Why did we sort the array first?
• What changes will you make if we have to find triplets with a given sum instead of 0?
• Why did we loop i from 0 to n-2 in the pseudo code?

2. Using Hash Set

We could use an unordered set data structure to store each value of the array. Set provides the benefit of searching an element in O(1) time. So, for each pair in the array, we will look for the negative of their sum that might exist in the set. If such an element is found then we could print the triplet which will be the pair of integers and the negative value of their sum.

Solution steps

• Run a loop from i=0 to n-2
• Create an empty hash set
• Run inner loop from j=i+1 to n-1
• If (0-(arr[i] + arr[j])) is present in the set then print arr[i], arr[j] and -(arr[i]+arr[j])

int[][] findTriplets(int arr[], int n) { 
    res[]
    for (int i = 0 to n-1) { 
        // find all pairs with sum equals to -arr[i] 
        set s
        for (int j = i+1 to n) { 
            x = -(arr[i] + arr[j])
            if (x is in s){ 
                temp[] = {x, arr[i], arr[j]}
                temp.sort()
                res.append(temp)
            } 
            else
                s.insert(arr[j])
        } 
    }
    return res
}

Complexity Analysis

Time Complexity: O(n²)

Space Complexity: O(n) (How?)

Critical Ideas to Think

• Do you think that sorting the temp array which consists of three elements affects the asymptotic time complexity?
• Which values we are storing in the set?
• Why are we creating a new set in each iteration of i loop?

3. Using Two Pointer Approach

The main idea is to iterate every number in arr.
We use the number as a target to find two other numbers which make total zero.
For those two other numbers, we move pointers, l and r, to try them.l start from left to right.
r start from right to left.

First, we sort the array, so we can easily move i around and know how to adjust l and r.

1. If the number is the same as the number before, we have used it as a target already, continue.
2. We always start the left pointer from i+1 because the combination of 0~i has already been tried.
3. Now we calculate the total:
   If the total is less than zero, we need it to be larger, so we move the left pointer.
4. If the total is greater than zero, we need it to be smaller, so we move the right pointer.
5. If the total is zero, then add it to our result
6. We need to move the left and right pointers to the next different numbers, so we do not get repeating result.
7. We do not need to consider i after arr[i] > 0, since the sum of 3 positive will be always greater than zero.
8. We do not need to try the last two since there are no rooms for l and r pointers.
   You can think of it as the last two have been tried by all others.

Pseudo Code

int[][] findTriplets(int arr[], int length) {
    res = []
    arr.sort()
    for(i = 0  to i < length - 2 ){                    // #[8]
	if(arr[i] > 0) 
            break                                  // #[7]
        if( i > 0 and arr[i] == arr[i-1])
            continue                               // #[1]
        l, r = i+1, length-1                       // #[2]
        while( l < r ){
            total = arr[i]+arr[l]+arr[r]
            if(total < 0)                          // #[3]
                l += 1
            else if (total>0)                      // #[4]
                r-=1
            else:                                  // #[5]
                res.append([arr[i], arr[l], arr[r]])
                while(l<r and arr[l]==arr[l+1]){   // #[6]
                    l += 1
                }
                while(l<r and arr[r]==arr[r-1]){   // #[6]
                    r -= 1
                }
                l += 1
                r -= 1
        }
    }
    return res
}

Complexity Analysis

Time Complexity: O(n²) (Why?)

Space Complexity: O(1)

Critical Ideas to Think

• Why there’s a while loop in # [6]? Do you think that we can remove these loops if the input array has no repeating elements?
• How we are updating the l and r pointers?
• Can you convert this algorithm to find triplets for a given sum instead of 0?

Comparison of Different Approaches

Suggested Problems to Solve

• Print all triplets with a given sum
• Count the triplets such that A[i] < B[j] < C[k]
• All unique triplets that sum up to a given value
• Count triplets with a sum smaller than a given value
• Number of unique triplets whose XOR is zero

If you have any more approaches or you find an error/bug in the above solutions, please comment down below.

Happy Coding! Enjoy Algorithms!