Combination Sum

Difficulty: Medium

Asked in: Amazon, Facebook, Adobe

Understanding The Problem

Problem Description

Given an array of integers arr[] and a target number k, write a program to find all unique combinations in arr[] such that the sum of all integers in the combination is equal to k.

Problem Note:

• All numbers (including target number k) will be positive integers.
• The same number may be chosen from arr[] the unlimited number of times.
• Elements in a combination (a1, a2, … , ak) must be in non-descending order. (i.e, a1 ≤ a2 ≤ … ≤ ak).
• The combinations themselves must be sorted in ascending order, i.e., the combination with the smallest first element should be printed first.
• The solution set must not contain duplicate combinations.

Example 1

Input: arr[] = [2, 3, 6, 7], k = 7 
Output:
[
  [7],
  [2,2,3]
]
Explanation: All the unique combinations whose sum is 7 is printed.
2+2+3 = 7
7 = 7 

Example 2

Input: arr[] = [2,3,5], k = 8 
Output:  
[   
    [2,2,2,2],   
    [2,3,3],   
    [3,5] 
]
Explanation: All the unique combinations whose sum is 8 is printed.
2+2+2+2 = 8
2+3+3 = 8
3+5 = 8

Backtracking Solution

First of all, we need to sort the array, to ensure the combination to be unique and also the numbers in the combination to be listed in a non-descending order.

Then, we define a recursive function with the signature as:

backtrack(int[][] res, int[] candidate, int [] nums, int target, int start)

where "candidate" is the list that we could take numbers from, "result" is the list of combination that we have accumulated so far, "start" is the starting point at which we could take numbers from forwards (no backward), and "target"is the rest sum that we need to achieve. A recursion tree for the above example might look like this →

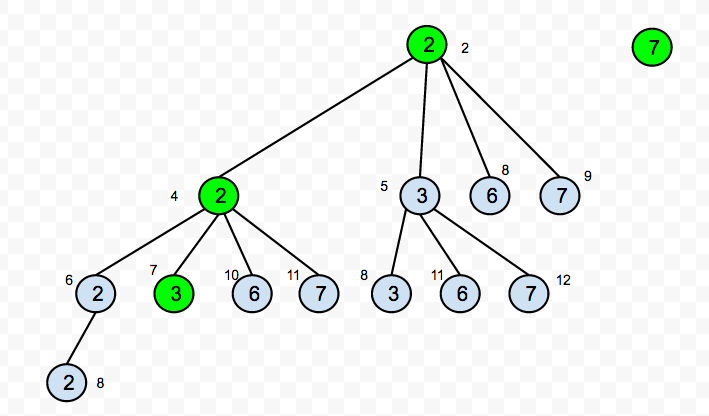
As a recursive function, the bottom cases for the backracking() are:

1. 1. The value of the start is equal to the target, we then find a combination, so just add the start to the result and output the result.
2. The value of the start is greater than the target, then it is impossible to find the combination onwards because the candidates the list is sorted and all the following elements would be greater than the target as well.

Given the above recursive function, we could solve the problem by calling the function for each candidate starting from the start point.
For each candidate, we first try to add the candidate into the result, and then again starting from this candidate, we call the backtracking() function to obtain the result for the new target afterwards.

Solution Steps

• Create a result array to store the valid sequences
• Create a curr array that will store the current sequence found in the path of the recursion tree.
• A backtrack function that will go into the recursion until the target is achieved, otherwise, it should backtrack to the previous phase as target becomes less than 0.
• At any point in time, if target becomes 0 then add the candidate array to the result as the values in the candidate array must be sum up to the given target.
• If those are not the cases then, one by one add the elements in the candidate array and recursively move forward.

Pseudo Code

int[][] combinationSum(int[] nums, int target) {
    int[][] result
    sort(nums)
    int[] curr
    backtrack(result, curr, nums, target, 0)
    return result
}

void backtrack(int[][] res, int[] candidate, int [] nums, int target, int start) {
    if(target < 0) 
        return
    else 
        if(target == 0) 
            res.add(candidate)
        else{
            for(int i = start; i < nums.length; i++) {
                candidate.add(nums[i])
                backtrack(list, candidate, nums, target - nums[i], i)
                // not i + 1 because we can reuse same elements
                candidate.remove(candidate.size() - 1)
            }
    }
}

Complexity Analysis

Time Complexity: O(l^k)

• Where l is the length of the array, k is the length of the longest possible combination (namely target / minInArray).
  i.e. If the min value in the array is 1, and the target is 9, the longest length of possible combination is 9 (9/1).

Space Complexity: O(k), for storing the path, which could be k long at most.

Critical Ideas To Think

• In the backtrack function why did we start the for loop from start than start + 1 ?
• If the question requires that the same number can be chosen only one time, then what change should we have to make in the pseudo code?
• What are the base cases of the recursion?
• Why we are appending the sequence to our result only when the target is equal to zero?
• Give a thought over the time complexity which is O(l^k).
• Find problems where you can apply a similar approach.

Suggested Problem To Solve

• Letter combination of a phone number
• Find a unique combination of unique numbers that sum up to target
• Search word in a matrix
• Print all permutations of a string

Happy Coding!

Team AfterAcademy!!