Find whether an array is a subset of another array - Interview Problem

Difficulty Level : Medium

Understanding the problem

Problem Description : Given two integer array A[] and B[] of size m and n(n <= m) respectively. We have to check whether B[] is a subset of A[] or not. An array B is a subset of another array A if each element of B is present in A. (There are no repeated elements in both the arrays)

For example

input : A[] = { 3, 5, 7, 12, 1, 9, 10, 0, 2 }, B[] = { 1, 3, 5, 9 }

Output : True (B[] is subset of A[])

Input : A[] = { 3, 5, 7, 12, 1, 9, 10, 0, 2 }, B[] = { 6, 3, 8 }

Output: False (B[] is not a subset of A[])

Possible follow-up questions to ask the interviewer :

• Can you modify the array? Yes, that's fine.
• Do we know something about the range of the numbers in the array? No, they can be arbitrary integers.
• Are the array elements necessarily positive? No, they can be positive, negative, or zero.
• Can the array contain duplicates? Sure, that's a possibility.

Designing efficient solutions

We are discussing four ways to solve this problem :

1. Brute force Approach: Using two loops
2. Sorting and binary search
3. Sorting and two Pointer approach
4. Using a Hash Table

1. Brute Force Approach: Using two loops

Search each element of B[] in A[] using linear search. If all elements of B[] is present in A[] then B[] is a subset of A[] else not.

Pseudo Code

int array_subSet (A[], B[], m , n)
{
    for ( i = 0 to n-1 )
    {
       for ( j = 0 to m-1 )
       { 
           if( B[i] == A[j] )
           break
       }
     if(j==m) 
       return -1
    }
 return 1
}

Complexity Analysis

There are two loops in the solution where one loop is running m times and other n times. So in the worst case, Time Complexity = O(mn), Space Complexity = O(1). But the critical question is - how can we improve the time complexity?

2. Sorting and binary search

If we sort array A[] then we can search each element of B[] in A[] using binary search. On the sorted array, Binary search performs searching in O(logn) which could help us to improve the time complexity.

Solution Steps

• Sort the array A[] in increasing order
• Search each element of B[] in sorted array A[] using binary search
• If the element is not found then return false.
• If all elements of B[] is present in A[] then return true

Pseudo Code

int array_subSet(A[], B[], m, n)
 {
     Sort(A, m)
     for (i= 0 to n-1)
     {
         x = binarySearch ( A, 0, n-1, B[i] )
         if ( x == -1)
            return -1
     }
 return 1
}

Complexity Analysis

For the implementation, Suppose we are using Heap Sort/merge sort and iterative binary search.

Time Complexity = Time complexity of sorting + n. Time complexity of Binary Search = O(mlogm) + n. O(logm) = O(mlogm + nlogm)

Space Complexity = Space Complexity of sorting + Space complexity of the binary search

If merge sort ,Space Complexity = O(m) + O(1) = O(m)

If Heap Sort, Space Complexity = O(1) + O(1) = O(1)

Critical Ideas to think!

• What will be the time and space complexity if we use quicksort? Compare different sorting algorithms
• iterative and recursive implementation of Binary search.
• Prepare a list of problems where you can apply the idea of sorting and binary search.

3. Sorting and two-pointer approach

If both A[] and B[] are sorted then we can apply the idea of two pointer approach of merge type process. In this approach, we start from the first element of both sorted arrays. At each step of the iteration, we compare one value from B[] with one value from A[] and move forward. On the basis of comparison, we can check if all elements of the sorted array B[] are found in sorted array A[].

Solution Visualization

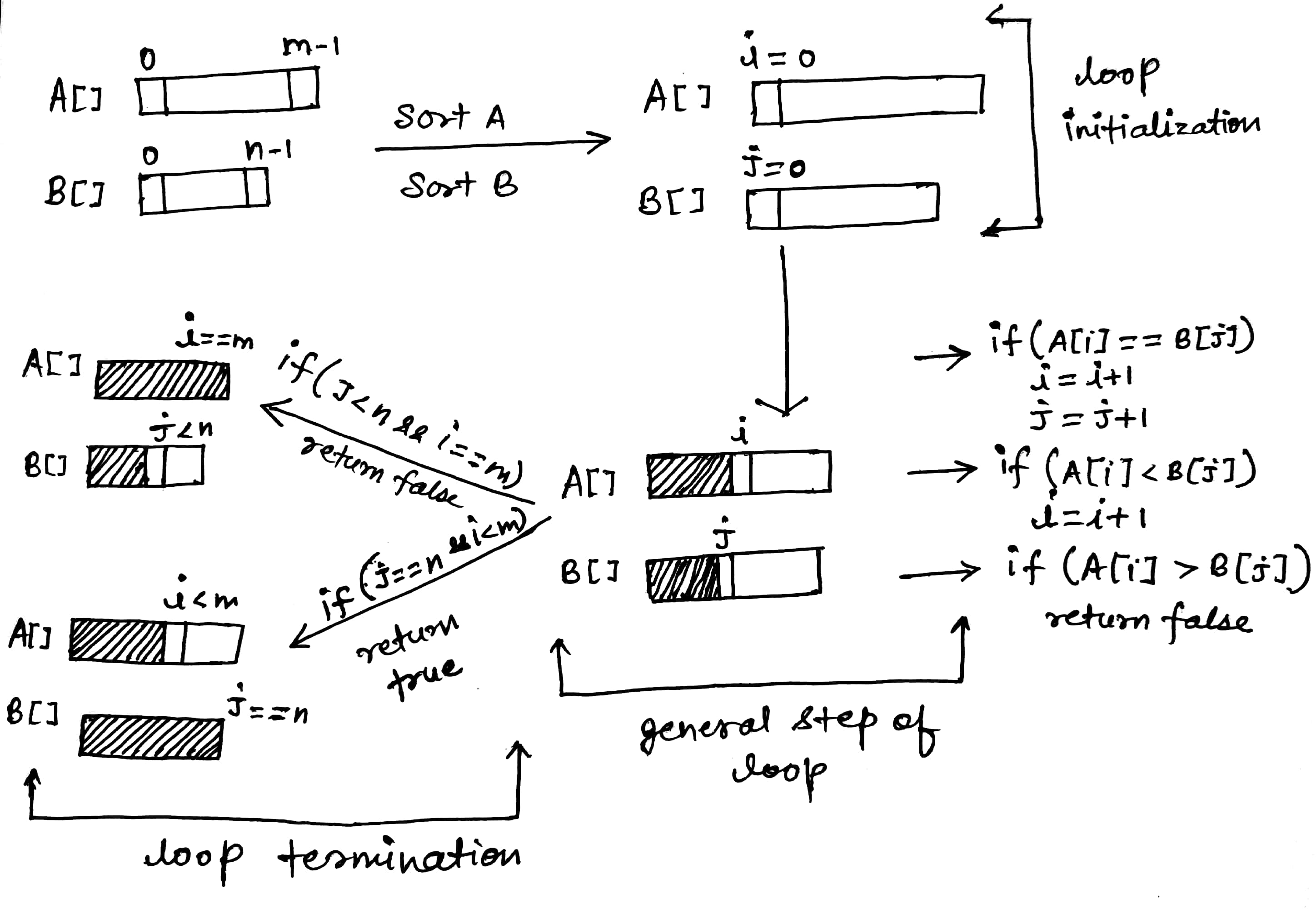
Solution Steps

1) Sort both the arrays in increasing order

2) Initialize the variables i and j in the sorted array A[] and B[] respectively. i = 0 and j = 0

3) Run a loop while i < m and j < n (Think about this loop)

• If (A[i] < B[j]) then increment the pointer i by 1 to search B[j] further in A[].
• if( A[i] == B[j] ) then increment both the pointers i and j by 1 because we have found a value common in both the array.
• if( A[i] > B[j]) then return false because we have found element B[j] which is not present in A[].

4) if (j<n) then return false otherwise return true (why?)

Pseudo Code

int array_subSet(A[], B[], m, n)
 {
     Sort(A,m)
     Sort(B,n)
     i = 0, j = 0 
     while (i < m && j < n )
     {
         if( A[i] < B[j] )
             i = i+1
         else if( A[i] == B[j] )
         {
             j = j+1
             i = i+1
         }
        else if( A[i] > B[j] )
            return -1
     }
 if (j<n)
    return -1
 else
    return 1
 }

Complexity Analysis

Suppose we are using Heap Sort or merge sort.

Time Complexity = Time complexity of sorting array A[] + Time Complexity of sorting array B[] + Time complexity of two pointer approach of merging (while loop) = O(mlogm) + O(nlogn) + O(m+n) = O(mlogm + nlogn)

If merge sort, Space Complexity = O(n)

If Heap Sort, Space Complexity = O(1)

Critical ideas to think!

• is this algorithm works fine if elements are repeated?
• Why time complexity of while loop is O(m+n) in the worst case?
• Prepare a list of problems where you can apply the idea of two pointer approach for the solution.

4. Using a Hash Table

Searching is a key operation here because we have to search for each value of B[] in A[]. So we can improve the time complexity by using an efficient data structure for searching operation. Hash Table is a perfect data structure which can perform searching and insertion efficiently in O(1) average.

Solution Visualisation

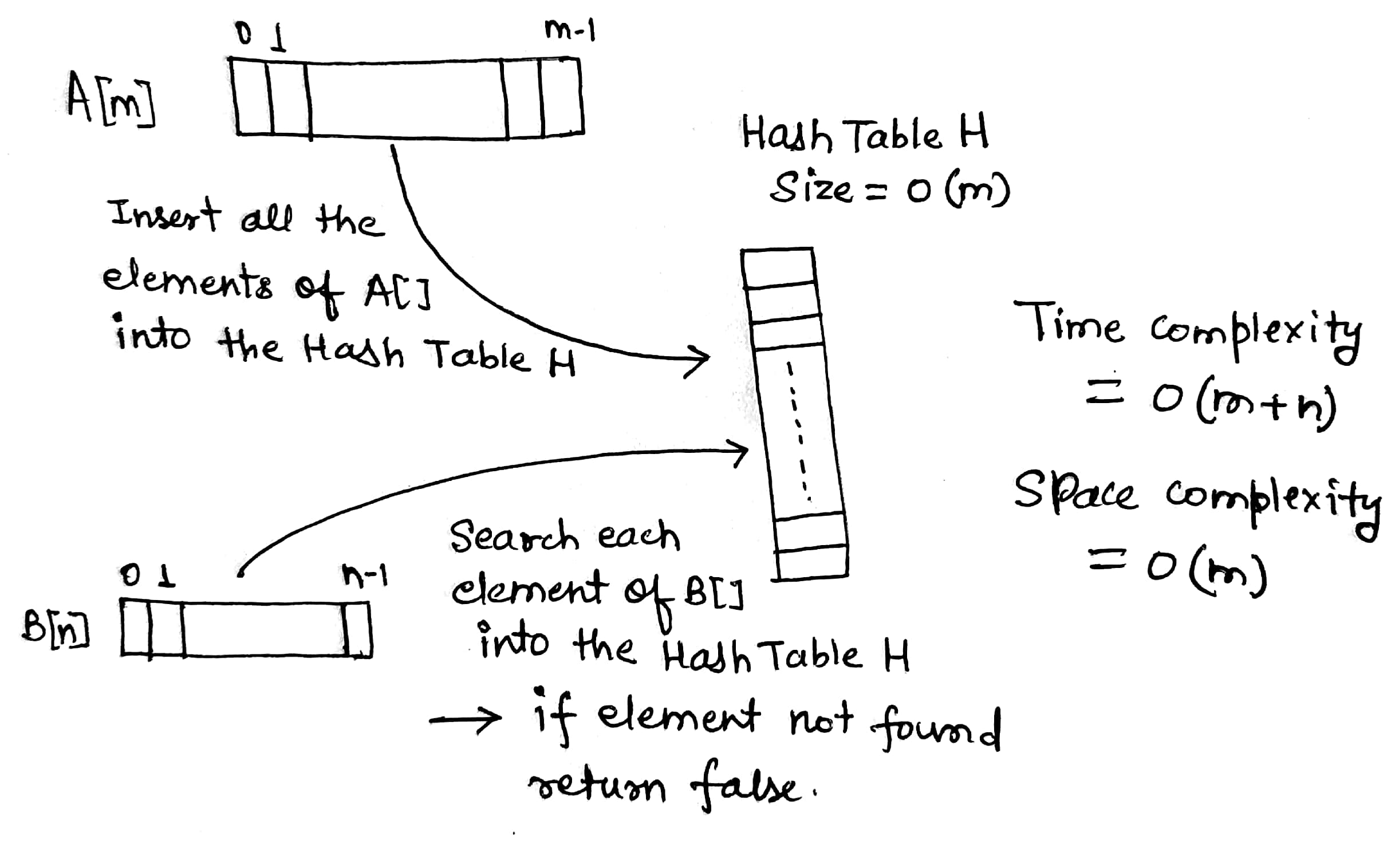
Solution Steps

• Take a Hash Table of size O(m)
• Insert all the elements of array A[] into the Hash Table
• Traverse B[] and search for each element of B[] in the Hash Table. If the element is not found then return 0.
• If all elements are found then return 1.

Pseudo Code

 int array_Subset(A[], B[], m, n)
   {
      Take HashTable H of Size m
      for(i = 0 to m-1)
      {
         H.insert(A[i])
      }
      for( i = 0 to n-1)
      {
         if(H.Search(B[i]) is false)
           return -1
      }
   return 1
   } 

Complexity Analysis

Time Complexity = Time complexity of inserting m elements of A[] in hash table + Time complexity of searching n elements of B[] in hash table = m. O(1) + n . O(1) = O(m) + O(n) = O(m+n)

Space Complexity = Extra space of Hash Table = O(m)

Critical ideas to think!

• is this algorithm works fine if elements are repeated?
• What will be the time and space complexity if we use BST in place of a hash table? Compare BST and Hash Table
• This is also a good example of problem-solving via data structure. Prepare a list of problems where we use data structures (hash table, BST, priority queue, stack, queue, etc) for the efficient solution.
• Is there any other way to solve this problem? Think.

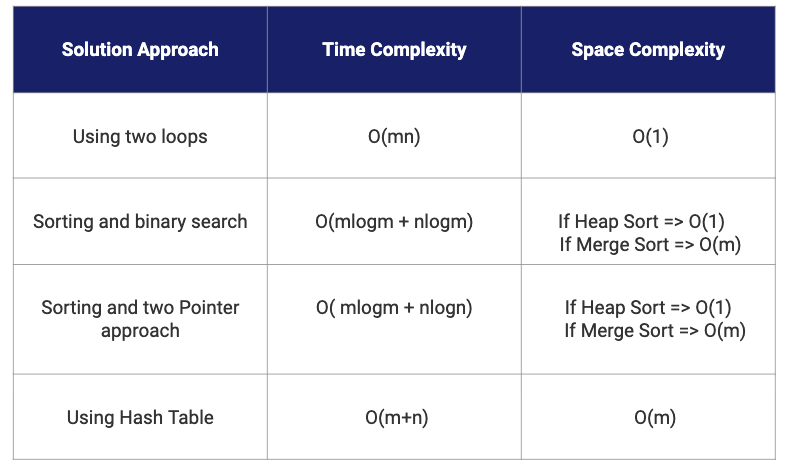
Comparison of the different solutions

Suggested Problems to solve

1. Given an array of n integers and given a number K, determines whether or not there exist two elements whose sum is exactly K
2. Given two unsorted arrays(elements in every array are distinct), find the intersection of two arrays
3. Given an unsorted array of integers, find the length of the longest consecutive sequence
4. Merge two sorted arrays

Please write comments if you find any error or bug. Happy Coding! Enjoy Algorithms!