Remove Nth Node From End of List

Difficulty: Medium

Asked in: Google, Amazon

Understanding the problem

Problem Description: You are given a linked list, write a program to remove the nth node from the end of the list and return the head.

Problem Note:

It is guaranteed that n ≤ length of linked list
Try to do this in one iteration.

Example 1

Input: 2->6->1->9, n=2
Output: 2->6->9

Example 2

Input: 1->2->3->4, n=4
Output: 2->3->4

Example 3

Input: 4->9->1->2, n=1
Output: 4->9->1

The node structure given to you will be→

class ListNode {
  int val;
  ListNode next;
  ListNode(int x) { val = x }
}

Solutions

We will be discussing three different solutions

Using Auxillary Space — By saving each node in an array
Making two passes through the list — remove the length- nth from the beginning.
Making one pass through the list — Using fast and slow pointers.

1. Using Auxillary Space

If we could save all the nodes in the array then, we could just remove the pointer of the (length-n-1)th node next to its next.next. In this way the nth node would be removed.

Pseudo Code

ListNode removeNthFromEnd(ListNode head, int n) {
    ListNode list[]
    ListNode curr = head
    while(curr!=null){
        list.append(curr)
        curr = curr.next
    }
    int size = size(list)
    if(size > 1){
        if(size > n){
            ListNode prev = list[size-n-1]
            ListNode  next = null
            if(n > 1){
                next = list[size-n+1]
            }
            prev.next = next;
        } else {
            head = list[1]
        }
        return head
    }
    return null
}

Complexity Analysis

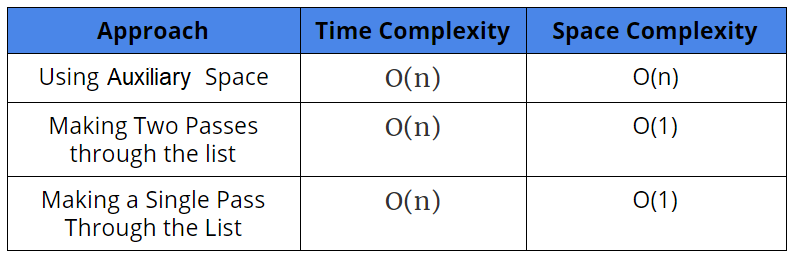
Time Complexity — O(n)

Space Complexity — O(n)

Critical Ideas to Thnik

Why we are storing each node in an array?
What will we return if the given value of n is 1?
Why did we set the list[size-n-1]th node next pointer with list[size-n+1] ?

2. Making two passes through the list

You can conclude from the previous approach that we don’t actually need to store the nodes in the array as we only need the length — n th node.

So, we could say that the problem is simply reduced to: Remove the ( L − n +1) th node from the beginning in the list, where L is the list length.

Solution Step

Create a “dummy” node, which points to the list head.
On the first pass, we find the list length L .
Set a pointer to the dummy node and start to move it through the list until it comes to the ( L − n )th node.
Relink the next pointer of the ( L − n )th node to the ( L − n +2)th node.

Pseudo Code

ListNode removeNthFromEnd(ListNode head, int n) {
    ListNode curr = head
    int end_index = 0
    while(curr) {
        end_index += 1
        curr = curr->next;
    }
    index_to_remove = end_index - n
    i = 0
    curr = head
    ListNode prev = nullptr
    while(i < index_to_remove) {
        prev = curr
        curr = curr.next
        i += 1
    }
    if(curr == head) {
        head = head.next
    }
    else if(prev) {
        prev.next = curr.next
    }
    delete curr
    return head
}

Complexity Analysis

Time complexity : O ( L ) where L is the length of the linked list.

Space complexity : O(1)

Critical Ideas to Think

What information about the list does the first pass give us?
What does the prev pointer represent here?
Can you dry run the above pseudo code with the above examples?

3. Making a single pass through the list

We could optimize the above approach where we only need a one-time traversal of the linked list. We could create two pointers, namely slow and a fast pointer pointing to the nodes that are n nodes apart from each other.

The fast pointer advances the list by n +1 steps from the beginning, while the slow pointer starts from the beginning of the list separating them by n nodes. We maintain this constant gap by advancing both pointers together until the fast pointer arrives past the last node. The slow pointer will be pointing at the n th node counting from the last. We relink the next pointer of the node referenced by the second pointer to point to the node’s next to the next node.

Solution steps

Create a fast and slow pointer pointing to n-1th and 0th node of the linked list
Start iterating over the linked list while updating the slow and fast pointers to its next.
When the loop terminates, then the fast pointer would be pointing to the last node and slow would be pointing to n-1th from the last node.
Set the next of slow pointer to its next of next
Now return the head.

Pseudo Code

ListNode* removeNthFromEnd(ListNode* head, int n) {
    ListNode fast = head
    ListNode dummy
    dummy->next = head
    ListNode slow = dummy
    int step_ahead = 0
    while(step_ahead < n-1){
        fast = fast.next
        step_ahead += 1
    }
    while(fast->next!=NULL){
        slow = slow.next
        fast = fast.next
    }
    //slow points to the node before target
    slow->next = slow->next->next
    return dummy->next
}

Complexity Analysis

Time complexity : O ( L ) where L is the length of the linked list.

Space complexity : O(1)

Critical Ideas to Think

What did we initialize the fast and slow pointers with and why?
How does the algorithm work if the given value of n is 1?
Can you dry run this algorithm for the above example and point out the difference between the single pass and double pass algorithms?