Graph Traversal: Depth First Search

For graph traversal, we normally use Breadth-First Search or Depth-First Search. In the last blog, we learned about Breadth-First Search. Now, in this blog, we will be learning about the other graph traversal algorithm i.e. Depth-First Search or DFS. So, let's get started.

What is a Depth-First Search?

Depth-First Search or simply DFS is a graph traversal algorithm that uses the concept of backtracking or exhaustive search.

In DFS, we keep on visiting the nodes until there is some neighbour node and if there is no neighbour node then we backtrack to the previous node and again we will visit all the nodes ahead of that node. This can also be performed with the help of the exhaustive search.

All you need to do is just select one path and traverse to the end of this path and after that, come back to the previous node and traverse the nodes that are connected to those nodes and this process is going to continue again and again until there is some node that is not traversed.

If we reach the end of one path, then we come back to the recently visited node. So, while writing the code for the DFS algorithm, we are going to use the Stack data structure because Stack uses the Last In First Out order i.e. LIFO order.

The following steps will be followed to implement the DFS:

• Select a starting/source node and add that node in the stack.
• Pop the top element of the stack and mark that node as visited. Push all the adjacent nodes of the top element in the stack.
• Repeat the above step until the stack is empty. Also, ensure that no visited nodes should be visited twice.

Now, let's look at the pseudocode of the above implementation:

DFS (G, s):                                   //here, G is the Graph and s is the source/starting node
      let S be the stack
      S.push( s )            //pushing source node in stack S 
      mark s as visited.
      while ( S is not empty):
          //Pop a node from the stack S
          v  =  S.top( )
          S.pop( )
          //Push all the neighbours of v in stack that are not visited   
         for all neighbours w of v in Graph G:
             if w is not visited :
                 S.push( w )         
             mark w as visited

Let's understand the above pseudocode with the help of one example:

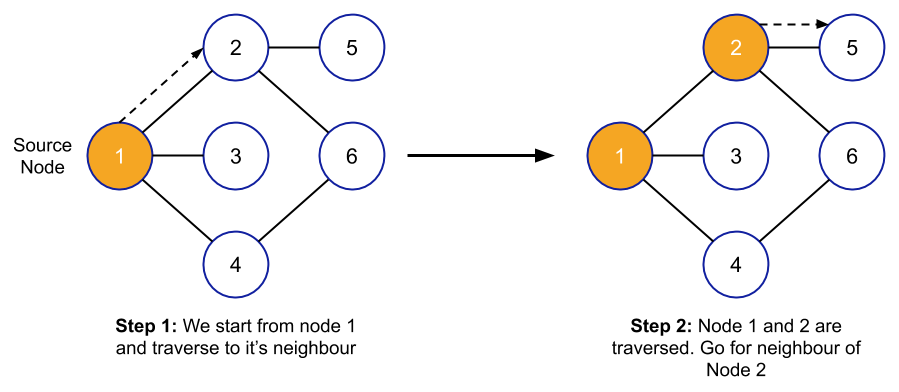
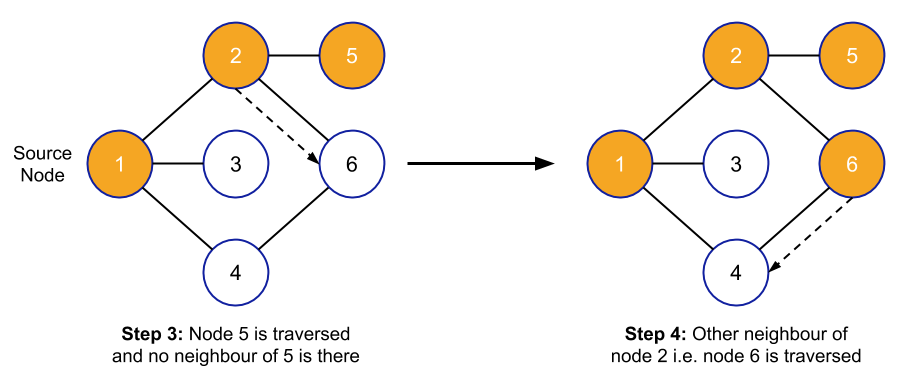
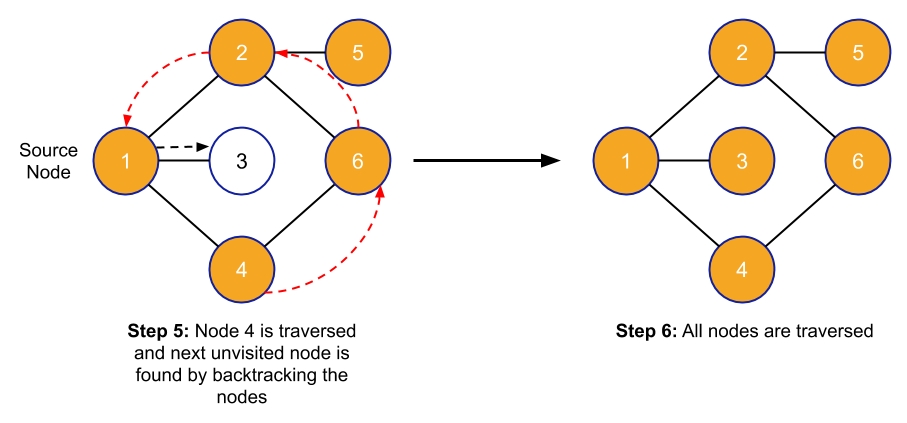
Application of DFS

• Minimum Spanning Tree: DFS of unweighted graph results in Minimum Spanning Tree.
• Bipartite Graph: DFS can be used to find if a graph is bipartite or not.
• Cycle detection: Since we are maintaining the list of visited nodes, it can be used to detect if a cycle is present in the graph or not.
• Topological Sorting: Topological Sorting can be done with the help of DFS.
• Strongly Connected Graph: Using DFS, we can find if a graph is strongly connected or not i.e. is there any path from one node to other nodes of the graph.

These are some of the applications of Depth-First Search.

Graph questions

• Is Graph Bipartite?
• Number of Islands
• Word Ladder Problem
• Smallest Multiple with 0 and 1
• Course Schedule
• Knight on Chessboard

Happy Learning, Enjoy Algorithms!

Team AfterAcademy!