Reverse Bits

Asked In: Amazon

Difficulty: Easy

Understanding The Problem

Problem Description

Given a non-negative integer num , write a program to return the number obtained after reversing the bits of num .

Problem Note:

The actual binary representation of the number is being considered for reversing the bits, no leading 0’s are being considered.

Example 1

Input: 13 
Output: 11 
Explanation: Binary representation of 13 is 1101. After reversing the bits we get 1011 which is equal to 11.

Example 2

Input: 6
Output: 3 
Explanation: Binary representation of 6 is 110.After reversing the bits we get 011 which is equal to 3.

Solution

Bit manipulation is an important concept and thus it explains how a number is stored in memory in the form of bits and how manipulating the bits will affect the value.

This problem requires the concept of bit manipulation, as the problem requires us to reverse the bits of a number.

Like in example 1, The binary of 13 is 1101 . if we reverse 1011 then we will get 1101 which is the binary of 11.

So, all we have to do is to convert the decimal number(base 10) into binary(base 2) and then reverse the binary number and then convert it into decimal. But knowing the fact that the computers stores any numerical value in a binary form inside the memory, so we can use the concept and perform bit manipulation.

Look at the below example:

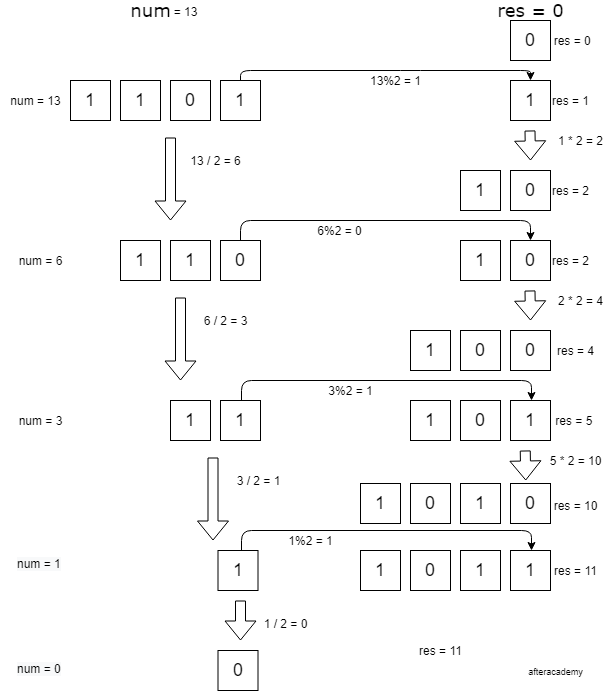
You will notice that each time we multiply res by 2, we basically shift the bits of res by one towards left. Similarly, each time we divide num by 2, we basically shift the bits of num by one towards the right. We can generalize the process of reversing the bits as shown above.

You may try the problem here.

Solution steps

To reverse the bits, we will perform the following operations

Create a variable res and initialize it with 0
If num > 0

Multiply res with 2
If num is odd then add 1 to res.
Divide num by 2.

3. Repeat step 2, until num > 0 .

4. Return res.

Pseudo Code

int reverseBits(int num) 
{ 
    int rev = 0
    // traversing bits of 'num' from the right 
    while (num > 0)
    { 
        // bitwise left shift  
        // 'res' by 1 
        res <<= 1     // multiply res by 2
        // if current bit is '1' or num is odd
        if (num & 1 == 1) 
            res ^= 1  // Convert 0 to 1
        // bitwise right shift  
        // 'num' by 1 
        num >>= 1     // divide num by 2
    }
    // required number 
    return res 
}

Complexity Analysis

Time Complexity: O(n), where n is the number of bits in num.

Space Complexity: O(1)

Critical Ideas To Think

How is the time complexity O(no. of bits)?
Instead of multiplying res by 2, we did res<<=1 , are these two same?
Instead of dividing num by 2 we did num>>=1 , are these two same?
How did we check if num is even or odd?
Besides doing the bit manipulation in another variable, can we create an integer array that would have stored the binary of num , and then we would have reversed the array and we could have used the values of the array to create a decimal integer? Then will this procedure would have worked? If yes, then will the complexity would be the same as of the above approach?