Greatest Common Divisor-Interview Problem

Greatest Common Divisor

Difficulty: Medium

Asked in: Google

Understanding the Problem:

Given two integers say A and B, you have to find the greatest common divisor or highest common factor of the given integers .

For example: INPUT: 10   15
             OUTPUT: 5
             
             INPUT: 36   48
             OUTPUT: 12

Explanation: 5 is the largest integer that is factor of both 10 and 15. Similarly, 12 is the largest integer that divides both 36 and 48 completely.

Possible follow-up questions to ask: →

Do we have negative numbers in the input?( Ans: No, only positive integers! )

Solutions

We are going to see two solutions to find the GCD or HCF of two numbers →

Brute Force Solution → This is a simple solution based on finding all the prime factors of both the numbers and choosing the common factors.
Euclidean Algorithm→ Euclidean algorithm helps us iterate towards the GCD in a much more optimized manner.
Optimized Euclidean Algorithm→ An optimization on standard Euclidean Operation to reduce time when numbers are big!

1. Brute Force Solution

Solution idea

The simple idea here is to find the factors of both the given numbers and then multiply the common factors to get the GCD.

Example: →

Factors of number 30: 2x3x5
Factors of number 20: 2x2x5
Since the common factors are 2x5, the GCD will be 2x5 = 10

Solution steps

We will start a loop from 1 and will go till the loop variable is smaller than both the numbers.
If the loop variable is dividing both the numbers completely, we will save this into result variable.
When the loop has finally terminated, the value stored in the result variable is the output.

Pseudo-Code

int getGCD(int number1, int number2)
{
   int result = 1
   for(int i=2 to min(number1,number2))
   {
      if( i % number1 == 0 and i % number2 == 0 )
          result=i
   }
   return result
}

Complexity Analysis

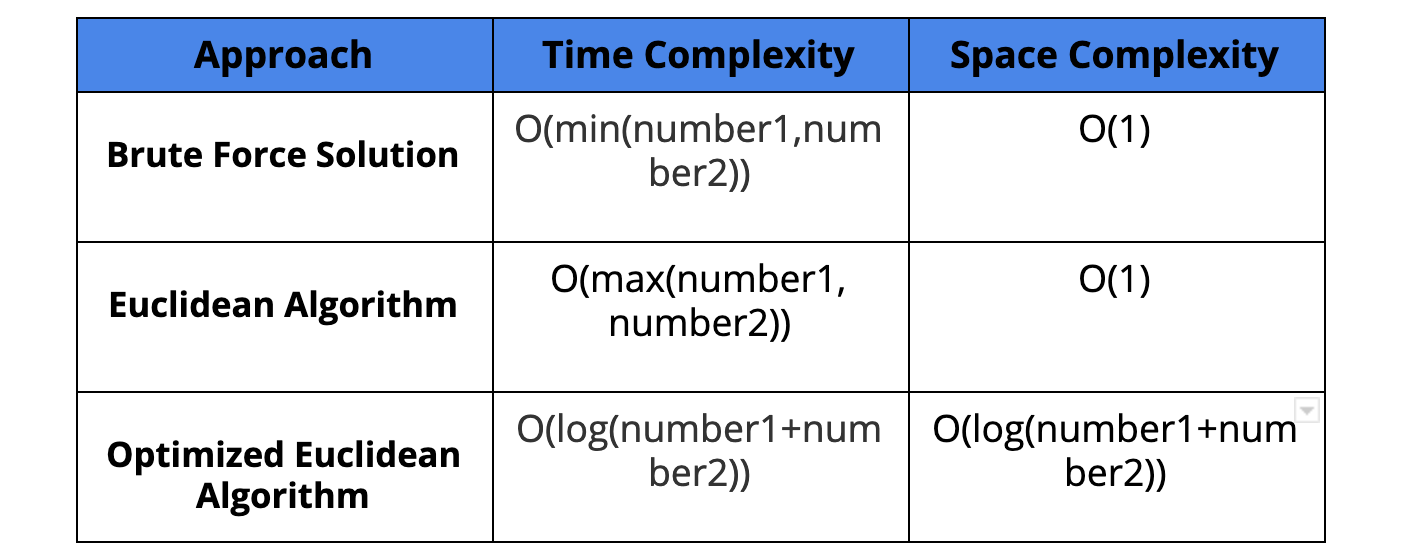
Time Complexity: O(min(number1,number2)) , that is the minimum among the two integers( Why?)

Space Complexity: O(1)

2. Euclidean Algorithm

We will see more efficient solution using euclidean algorithm for GCD.

Solution idea

Euclidean Algorithm is based on the principle that the GCD of two numbers remains the same if the larger of the two numbers is replaced by its difference with the smaller number. This process keeps reducing the larger number until the number becomes equal to the smaller number. When this happens, we get the GCD.

Solution steps

We will keep reducing the larger number among the two numbers by the difference between the two, until both become equal and we get the GCD.

Pseudo-Code

int getGCD(int number1, int number2)
{
   while(number1 != number2)
   {
     if( number1 > number2 )
       number1 = number1 - number2
     else
       number2 = number2 - number1
   }
   return number1
}

Complexity Analysis

Time Complexity: O(max(number1, number2))

(Why? Hint: Consider the case when there is a large difference between the numbers )

Space Complexity: O(1)

★ Can you think of optimizing the Euclidean Algorithm? Can we replace the subtraction with some more efficient operators?

3. Optimized Euclidean Algorithm

Solution idea

The problem with the above algorithm is the repetitive calculation(subtraction) in the case when one of the numbers is very large. To avoid this, we can change the subtraction operation with division. The algorithm will end once zero remainder is found.

Solution steps

We will replace the larger number with the remainder of the division between the larger number and smaller number.
If the remainder is zero, we have the GCD.

Pseudo-code

int getGCD(int number1, number2)
{
   if( number2 == 0 )
       return number1
   return getGCD(number2, number1%number2)
}

Complexity Analysis

Time Complexity: O(log(number1+number2)) (Why?)

Space Complexity: Think! ( Hint: What is the recursive stack space used?)

Critical ideas to think!

Can you think of different properties of GCD and it’s relation with LCM?
Analyze more about the complexity of the optimized Euclidean Algorithm.
How can we find GCD for negative integers? What about floating point numbers??
What about the complexity when iteratively implementing optimized Euclidean code?