Merge K Sorted Lists

Asked in: Amazon, Google, Microsoft

Difficulty: Hard

Understanding the Problem

Problem Description: Merge k sorted linked lists and return it as one sorted list.

Example :

You have to return the head of the first node after merging k lists. The node structure passed to your function will be

class ListNode
{
    int val
    ListNode next
}

Hint → Let's keep a pointer for every linked list. At any instant, you will need to know the minimum of elements at all pointer. Following it you will need to advance that pointer. Can you do this in complexity better than O(K)?

Brute force and efficient solutions

We will be discussing five different approaches to solve the problem:

1. Brute Force Solution — Putting all the nodes in an array and sort them.
2. Compare one by one — One by one compare all the head nodes of the k lists and add it to the result list.
3. Maintaining a Priority Queue — Optimize approach 2 by using a priority queue.
4. Merge lists one by one — Update the references of the node to merge two lists at a time. Do this operation for k-1 times.
5. Divide and Conquer — Pair up K lists and merge each pair.

1. Brute Force Solution

The idea is to insert all the node values from all the k lists into an array. Sorting the array and creating a new linked list from the sorted array will give the required output.

Solution Steps

• Traverse all the linked lists and collect the values of the nodes into an array.
• Sort and iterate over this array to get the proper value of nodes.
• Create a new sorted linked list and extend it with the new nodes.

Pseudo Code

ListNode mergeKLists(ListNode[] lists, int k)

{
    // x array to store all the values from lists
    int x[]
    for(i = 0 to k) 

    {
        ListNode temp = lists[i]
        while(temp is not null)

       {
            // append the value of temp to x
            x.add(temp.val)
            temp = temp.next
        }
    }
    // sort all the values of x
    sort(x)
    // Head node to return
    ListNode head(-1)
    ListNode temp = head
    for(i = 0 to x.size()) {
        ListNode newVal(x[i])
        temp.next = newVal
        temp = temp.next
    }
    return head.next
} 

Complexity Analysis

Time complexity: O(NlogN) where N is the total number of nodes. Collecting all the values costs O(N) time.

Space complexity: O(N). Creating a new linked list costs O(N) space.

Critical Ideas to Think

• Why did we sort the x array?
• Why we are returning head.next instead of the head?
• Is it important for the input lists to be sorted for this approach?
• Do you think of a better way to optimize space complexity?

2. Compare One by One

All the given lists are sorted, which means that the head of each list would be the smallest element in its chain. So we could extract the minimum from the k head nodes and append it to the result list.

Solution Steps

• Compare every k nodes (head of every linked list) and get the node with the smallest value.
• Extend the final sorted linked list with the selected nodes.

Pseudo Code

ListNode mergeKLists(ListNode[] lists, int k) {
    int min_index = 0
    ListNode head(0)
    // reference pointer pointing to head
    ListNode ref = head
    while (true) {
        bool isBreak = true
        int min = INT_MAX
        for (i = 0 to k) {
            if (lists[i] is not null) {
                if (lists[i].val < min) {
                    min_index = i
                    min = lists[i].val
                } 
                isBreak = false
            }
        }
        if (isBreak) {
            break
        } 
        ListNode a(lists[min_index].val)
        ref.next = a
        ref = ref.next 
        lists[min_index] = lists[min_index].next
    }
    ref.next = NULL
    return head.next
}

Complexity Analysis

Time complexity: O(kN) where k is the number of linked lists.Almost every selection of nodes in final linked costs O(k) (k-1 times comparison).

Space complexity: O(n) Creating a new linked list costs O(n) space.

Critical Ideas to Think

• Can you visualize how we are appending to the reference pointer?
• How did we check if there are no nodes to visit in the linked list in an iteration?
• Do you think of a case when the actual time complexity could be more than O(kN) using this approach?
• Can you find out a way to optimize the space complexity to O(1) using this approach?

Pseudo Code

ListNode mergeKLists(ListNode[] lists, int k) {
    int min_index = 0
    ListNode head(0)
    // reference pointer to head
    ListNode ref = head
    while (true) {
        bool isBreak = true
        int min = INT_MAX
        for (int i = 0 to k) {
            if (lists[i] is not null) {
                if (lists[i].val < min) {
                    min_index = i
                    min = lists[i].val
                }
                isBreak = false
            }
        }
        if (isBreak) {
            break
        } 
        ref.next = lists[min_index]
        ref = ref.next
        lists[min_index] = lists[min_index].next
    }
    ref.next = null
    return head.next
}

Complexity Analysis

Time complexity: O(kN) where k is the number of linked lists.Almost every selection of nodes in final linked costs O(k) (k-1 times comparison).

Space complexity: O(1) (Why?)

Critical Ideas to Think

• Do you think that the two pseudo-codes are the same in Compare one by one approach?
• What changes did we make to optimize the space with respect to the previous code?
• How is space complexity is O(1)?
• Why are we returning head.next instead of the head?
• Can you find a way to optimize the time complexity?

3. Maintaining a Priority Queue

Solution Steps

1. Create a priority queue.
2. Insert the first node from all the lists into the priority queue.
3. Loop until the priority queue is not empty

• Extract the minimum node from the queue and add it to our result list.
• Add the next node (if present) from the extracted node list.

4. Return the resultant list.

Pseudo Code

int cmp(ListNode node1, ListNode node2) {
    return node1.val - node2.val
}
ListNode mergeKLists(ListNode[] lists, int k) { 
    // priority Queue Q of type ListNode and comparator cmp
    PriorityQueue Q(cmp)
    for(int i = 0 to k){
        if(lists[i] is not null){
            Q.add(lists[i])
        }        
    }
    ListNode head(0)
    ListNode ref = head
    while(Q is not empty){ 
        // fetch first element of queue
        ref.next = q.poll()
        ref = ref.next
        ListNode next = ref.next
        if(next is not null){
            q.add(next)
        }
    }
    return head.next
}

Complexity Analysis

Time complexity: O(Nlogk) (How?) where k is the number of linked lists.

• The comparison cost will be reduced to O(log k) for every pop and insertion to a priority queue. But finding the node with the smallest value just costs O(1) time.
• There are N nodes in the final linked list.

Space complexity: O(n) Creating a new linked list costs O(n) space.

Priority queue (often implemented with heaps) costs O(k) space.

Critical Ideas to Think

• How does the priority queue work?
• Why does the comparison cost reduced to O(log k)?

4. Merge lists one by one

Convert merge k lists problem to merge 2 lists (k-1) times.

You may refer to this merge 2 lists problem page for an explanation of the approach.

Following the concept of merging two lists, we can merge all the k lists taking two lists at a time.

Pseudo Code

ListNode mergeTwoSortedLists(ListNode A, ListNode B)
{
    if(A == NULL)
        return B
    if(B == NULL)
        return A
    ListNode output = NULL   
    if(A.val < B.val)
    {
        output = A
        A = A.next
    }
    else
    {
        output = B
        B = B.next
    }
    ListNode curr = output
    while(A != NULL && B!= NULL)
    {
        if(A.val > B.val)
        {
            curr.next = B
            B = B.next
        }
        else
        {
            curr.next = A
            A = A.next
        }
        curr = curr.next
    }
    if(A!= NULL)
        curr.next = A
    if(B!= NULL)
        curr.next = B 
    return output
}

ListNode mergeKLists(ListNode[] lists, int k) {
    if(k==1){
        return lists[0];
    }
    if(k==0){
        return null;
    }
    ListNode head = mergeTwoSortedLists(lists[0],lists[1])
    for (int i = 2 to k) {
        head = mergeTwoSortedLists(head,lists[i])
    }
    return head
}

Complexity Analysis

Time complexity: O(kN)(How?) where k is the number of linked lists.

We can merge two sorted linked lists in O(n) time where n is the total number of nodes in two lists.

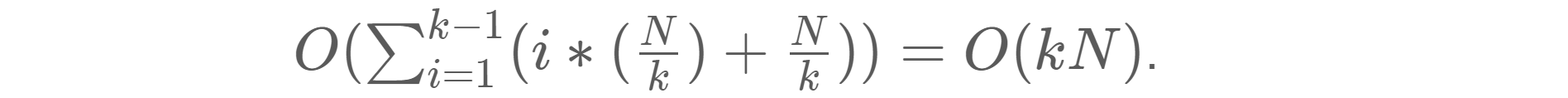
Space Complexity: O(1). We can merge two sorted linked list in O(1) space.

Critical Ideas to Think

• What are the different approaches to merge two lists?
• Can you figure out the proof of the time complexity to be O(kN) for this approach?
• Do you think that merging the linked lists according to the concept of divide and conquer could optimize the time complexity?

5. Divide and conquer

We don’t need to traverse most nodes many times repeatedly.

• Pair up k lists and merge each pair.
• After the first pairing, k lists are merged into k/2 lists with average 2N/k length, then k/4, k/8 and so on.
• Repeat this procedure until we get the final sorted linked list.

Thus, we’ll traverse almost N nodes per pairing and merging, and repeat this procedure about log​k times.

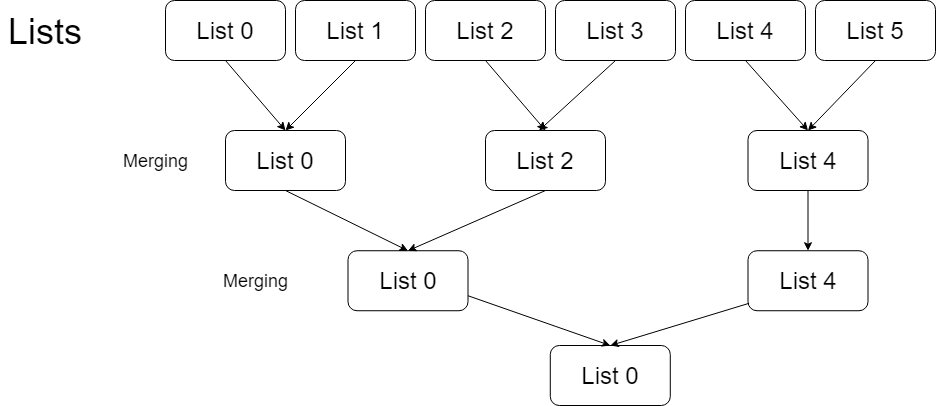
Pseudo Code

ListNode mergeTwoSortedLists(ListNode A, ListNode B)
{
    if(A == NULL)
        return B
    if(B == NULL)
        return A
    ListNode output = NULL   
    if(A.val < B.val)
    {
        output = A
        A = A.next
    }
    else
    {
        output = B
        B = B.next
    }
    ListNode curr = output
    while(A != NULL && B!= NULL)
    {
        if(A.val > B.val)
        {
            curr.next = B
            B = B.next
        }
        else
        {
            curr.next = A
            A = A.next
        }
        curr = curr.next
    }
    if(A!= NULL)
        curr.next = A
    if(B!= NULL)
        curr.next = B 
    return output
}

ListNode mergeKLists(ListNode[] lists, int k) {
    if(k == 0){
        return null
    }
    int interval = 1
    while(interval < k){
        int i = 0
        while(i + interval < k) {
            lists[i]= mergeTwoSortedLists(lists[i], lists[i+interval])
            i = i + interval * 2
        }
        interval *= 2
    }
    return lists[0]
}

Complexity Analysis

Time complexity: O(Nlogk)(How?) where k is the number of linked lists.

We can merge two sorted linked lists in O(n) time where n is the total number of nodes in two lists.

Sum up the merge process and we can get →

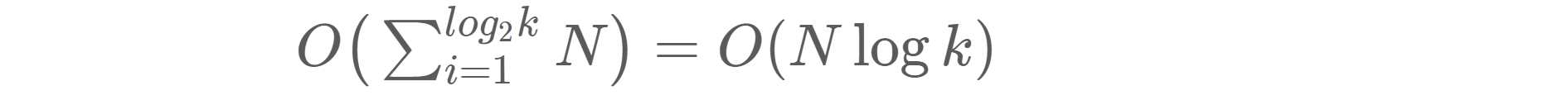
Space complexity: O(1)

Critical Ideas to think

• Are you able to visualize how we are merging the lists?
• Are you able to prove the time complexity to be O(Nlogk) for this approach?
• How the space complexity is O(1)?
• Do you think the case is handled here when k is odd?

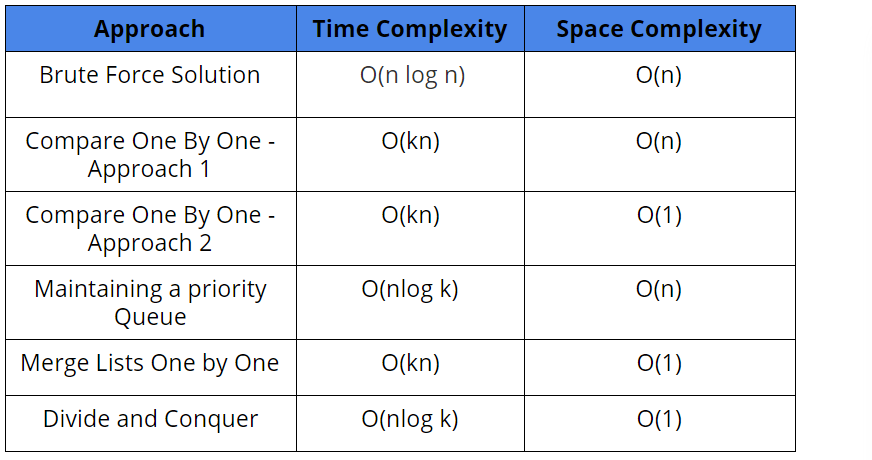
Comparison of Different Solutions

Similar Problems to Solve

• Merge sort in the linked list.
• Insertion sort in the linked list.
• Merge K sorted array.
• Merge 2 sorted lists.

If you have any more approaches or you find an error/bug in the above solutions, please comment down below.

Happy Coding! Enjoy Algorithms!