Merge Two Sorted Lists - Interview Problem
AfterAcademy Tech
•
04 Dec 2019

Difficulty: Easy
Asked in: Amazon, Microsoft, Yahoo
Understanding the Problem
Problem Description: Merge two sorted linked lists and return the head of the new sorted list.
For Example
Input: A = 1->2->4 and B = 1->3->4
Output: 1->1->2->3->4->4
Input: A = 6->25 and B = 1->3->4
Output: 1->3->4->6->25
The node structure for the Linked List passed to your function will be
class ListNode {
int val
ListNode *next
ListNode(int v)
{
val = v
next = NULL
}
}
Possible follow-up questions to ask the interviewer:-
- Is it possible that both linked lists are of different sizes? (Ans: Yes)
- Is it possible that one of the lists is empty? (Ans: Yes, You need to handle these cases.)
- Can, we modify the list? (Ans: Yes)
Solutions
We are discussing four ways to solve this problem:
- Brute Force: Combine and then sort.
- Iterative Merging: Using two pointer approach.
- Recursive Merging: Merge using recursion.
- Iterative In-place: Update the references of the node to merge.
1. Brute Force Approach
The basic idea is to combine both the lists and sort the final list to get the output. So to combine the list, we will append the second list at the end of the first list.
Pseudo-Code
ListNode mergeTwoSortedLists(ListNode A, ListNode B)
{
if(A == NULL)
return B
if(B == NULL)
return A
ListNode temp = A
while (temp.next != NULL)
{
temp = temp.next
}
temp.next = B
sort(A)
return A
}
Complexity Analysis
The overall complexity of the above algorithm will depend on the complexity of the sorting algorithm. Here we are using the insertion sort algorithm for sorting (M+N) size linked list.
Time Complexity = Combine both linked lists + Sort the final list.
= O(M) + O((M+N)²) (Why?) = O((M+N)²)
Space Complexity = O(1) (Using Insertion Sort will take O(1) space)
Critical ideas to think!
- Can we use the sorted property of both linked lists to improve the time complexity?
- Which is the fastest algorithm for sorting a linked list: Insertion Sort, Merge sort or Quick-sort? Implement and Compare the time & space complexities.
2. Iterative Merging
The idea behind this solution is to use the sorted property and iterate over both the lists using two pointers. During this, we compare the values of both nodes and put the smaller value in the dummy node which will be appended in the output list.
Solution Step
- If one of the lists is empty return the other.
- Initialize a node output = NULL, which will the head of the merged list. Compare the first element of both list and create a dummy node temp which stores the smaller value and make output referencing to it.
- If A.val < B.val, create a dummy node temp and set output = temp and A = A.next.
- Else, create a dummy node temp and set output = temp and B= B.next.
3. Initialize a pointer curr = output and Iterate till any of the lists reaches its end. Compare the current node’s value of both the list
- If A.val < B.val, create a dummy node temp and set curr.next = temp and B= B.next.
- Else, create a dummy node temp and set curr.next = temp and A= A.next
- Move the curr pointer, curr = curr.next.
4. If list A reaches its end in the above loop then append the remaining node of B into the output list (or vice versa).
5. Return output.
Pseudo-Code
ListNode mergeTwoSortedLists(ListNode A, ListNode B)
{
if(A == NULL)
return B
if(B == NULL)
return A
ListNode output = NULL
if( A.val < B.val)
{
ListNode temp = ListNode(A.val)
output = temp
A = A.next
}
else
{
ListNode temp = ListNode(A.val)
output = temp
B = B.next
}
ListNode curr = output
while(A != NULL && B!= NULL)
{
if(A.val > B.val)
{
ListNode temp = ListNode(B.val)
curr.next = temp
B = B.next
}
else
{
ListNode temp = ListNode(A.val)
curr.next = temp
A = A.next
}
curr = curr.next
}
while(A!= NULL)
{
ListNode temp = ListNode(A.val)
curr.next = temp
A = A.next
curr = curr.next
}
curr.next = A
while (B!= NULL)
{
ListNode temp = ListNode(B.val)
curr.next = temp
B = B.next
curr = curr.next
}
return output
}
Complexity Analysis
Time Complexity: O(N+M) where N and M are the sizes of linked lists.
Space Complexity: O(N+M), creating dummy nodes.
Critical ideas to think!
- Is there any way to do it without using extra space?
- Think about the worst case and best case of the above approach?
3. Recursive Merging
The idea is to compare the current node of both the lists and add a node with smaller value to the output list. After this, let the recursion handle the merging of the remaining list.
Pseudo-Code
ListNode mergeTwoSortedLists(ListNode A, ListNode B)
{
if(A == NULL)
return A
if(B == NULL)
return B
ListNode output = NULL
if (A.val < B.val)
{
output = A
A.next = mergeTwoSortedLists(A.next,B)
}
else
{
output = B
B.next = mergeTwoSortedLists(A,B.next)
}
return output
}
Complexity Analysis
Time Complexity: O(M+N), At every call of recursion, we are adding one node to the output.
Space Complexity: O(M+N), Stack space will be used in recursion.
Critical ideas to think!
- Compare both iterative and recursive approaches?
4. Iterative In-place
The idea is just similar to the 2nd approach we discussed, just modify the list. Instead of making the new dummy node, just store the reference of the node of A and B.
Solution Step
- If one of the lists is empty return the other.
- Create variable output and initialize it with whichever list has the smaller first element.
- Initialize curr = output, which we will use to iterate the output list, store the reference to the last element in output.
5. Iterate until any of the lists reaches its end.
6. Compare the values of current nodes in both lists
- If A.val < B.val, set curr.next = A and set A = A.next.
- Else, set curr.next = B and set B = B.next.
7. Set curr = curr.next
8. Now append the remaining nodes of the list which has not been fully iterated.
- if A != NULL, set curr.next = A.
- if B != NULL, set curr.next = B.
9. Return output.
Pseudo-Code
ListNode mergeTwoSortedLists(ListNode A, ListNode B)
{
if(A == NULL)
return B
if(B == NULL)
return A
ListNode output = NULL
if(A.val < B.val)
{
output = A
A = A.next
}
else
{
output = B
B = B.next
}
ListNode curr = output
while(A != NULL && B!= NULL)
{
if(A.val > B.val)
{
curr.next = B
B = B.next
}
else
{
curr.next = A
A = A.next
}
curr = curr.next
}
if(A!= NULL)
curr.next = A
if(B!= NULL)
curr.next = B
return output
}
Complexity Analysis
Time Complexity: O(N+M) where N and M are the sizes of linked lists.
Space Complexity: O(1)
Critical ideas to think!
- Does the approach need to be changed for the same size or different size linked lists?
- Compare the above approaches by analyzing them using examples.
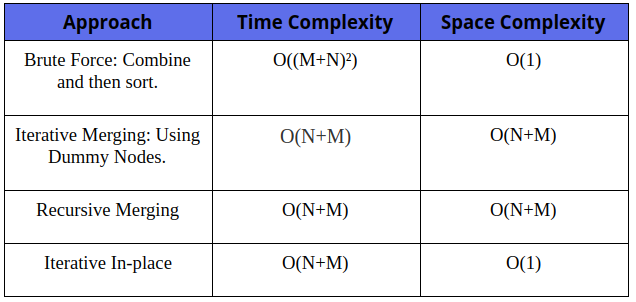
Comparison of different solutions
Suggested problems to solve
- Merge k Sorted Lists.
- Merge sort in the linked list.
- Insertion sort in the linked list.
- Merge 2 sorted array.
- Sorted merge of two sorted doubly circular linked lists.
If you have any more approaches or you find an error/bug in the above solutions, please comment down below.
May the code be with You!
Enjoy Algorithms!
AfterAcademy Data Structure And Algorithms Online Course — Admissions Open
Written by AfterAcademy Tech
Share this article and spread the knowledge
Read Similar Articles
AfterAcademy Tech
Sort List - Merge Sort
Sort a linked list using Merge Sort. This is a very famous interview problem that demonstrates the concept of recursion. This problem is quite similar to Merge Sort in Arrays.

AfterAcademy Tech
Merge two Binary Trees - Interview Problem
This is an interview problem asked in companies like Amazon, Microsoft. The problem is to merge two binary trees. The overlapping nodes are replaced by the sum of corresponding nodes. We are discussing two ways of solving this.

AfterAcademy Tech
Sort a linked list using Insertion Sort - Interview Problem
Sort a linked list using insertion sort and return its head.

AfterAcademy Tech
Add Two Numbers as Lists - Interview Problem
You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order and each of their nodes contains a single digit. Add the two numbers and return it as a linked list.
