Maximal Square

Asked in: Medium

Difficulty: Google, Microsoft

Understanding The Problem

Problem Description

You are given a 2D binary matrix arr[][] filled with 0's and 1's. The array contains a square of 1's. So, you need to find that square and return its area.

Example 1

Input: 
1 1 1 1 0
1 1 1 1 1
1 1 1 1 1
1 0 1 0 0
Output: 9
Explanation: The largest square in the given matrix has an area of 9 sq. units.

Example 2

Input: 
0  0  0  0  1  1
0  1  1  1  1  0
0  1  1  1  1  0
0  1  1  1  1  0
1  1  1  1  1  1
1  0  0  0  0  0
Output: 16
Explanation: The largest square in the given matrix has an area of 16 sq. units.

Narrowing down, the problem simply asks for the maximum length of the side of a square that can be noticed in the input matrix. In other words, the largest set of connected ones that forms a square.

Solutions

We will be discussing three solutions from brute force to the most optimized approach

1. Brute Force → For each occurring 1's in the given matrix, move diagonally towards the bottom right while checking the rows and columns contains only 1's.
2. Dynamic Programming → Create a DP array whose each element dp[i][j] will store the side length corresponding to the maximum square considering mat[i][j] as the bottom right cell of the square.
3. Space Optimized DP → Try to use a 1D DP array following the similar elements of DP as of approach 2.

You may try this problem yourself from here.

1. Brute Force

A straight forward solution will be finding out every possible square of 1’s and return the area of the biggest square.

To find all possible squares, we will start searching for 1’s in the input matrix from the top left, and for each occurrence of 1 for some mat[i][j], we will start descending through the diagonal to the bottom right in search of squares and thereby we will keep updating maxSideLength.

For 0’s we don’t need to search for squares as the question demands the max square area consisting of only 1's.

More formally, for each mat[i][j] = 1, goto mat[i+1][j+1] and check that the corresponding row and column only consist of 1’s and then goto mat[i+2][j+2] and repeat the process until the condition fails.

Solution Steps

For each matrix[i][j] = 1

• Set sqlen with 1 and k with j
• Check the row matrix[i][j+sqlen] … matrix[i+sqlen][j+sqlen] and the column matrix[i+sqlen][j] … matrix[i+sqlen][j+sqlen] are only consist of 1’s.
• Increment sqlen, otherwise move to some other matrix[i][j] while storing the maxSqLen .

Pseudo Code

int maximalSquare(char[][] matrix) {
    rows = matrix.length
    cols = matrix[0].length
    maxsqlen = 0
    for (int i = 0 to i < rows) {
        for (int j = 0 to j < cols) {
            if (matrix[i][j] is '1') {
                sqlen = 1
                bool isOkay = true
                while(sqlen + i < rows and sqlen + j < cols and isOkay) {
                    for (int k = j to k <= sqlen + j) {
                        if (matrix[i + sqlen][k] is '0') {
                            isOkay = false
                            break
                        }
                    }
                    for (int k = i to k <= sqlen + i) {
                        if (matrix[k][j + sqlen] is '0') {
                            isOkay = false
                            break
                        }
                    }
                    if (isOkay)
                        sqlen = sqlen + 1
                }
                if (maxsqlen < sqlen) {
                    maxsqlen = sqlen
                }
            }
        }
    }
    return maxsqlen * maxsqlen
}

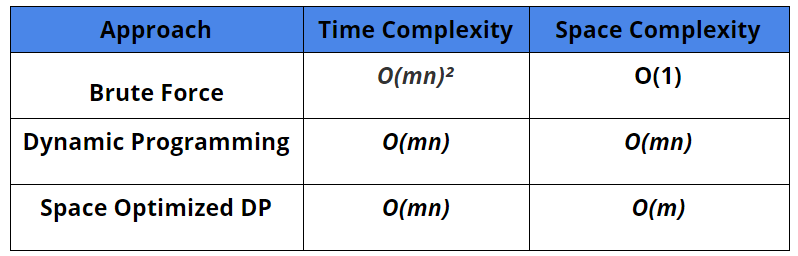
Complexity Analysis

Time Complexity: O(mn)²

Space Complexity: O(1)

Critical Ideas To Think

• Why didn’t we looked for some index k,l for each i,j indices with matrix[i][j] = 1 in search of squares of 1’s instead of moving diagonally downward? Yes, That will also be a solution, can you guess what would be the time complexity in that case?
• What role does isOkay variable playing?
• While we were incrementing sqlen variable moving downward, though it was representing the square length with respect to i,j . How?

2. Dynamic Programming

We define dp[i][j] the maximal ending at position (i, j). Thus, the current state (dp[i][j]) depends on the left (dp[i][j - 1]), up (dp[i - 1][j]), and left-up's (dp[i - 1][j - 1]) states.

The current state equals to the minimum of these three states plus matrix[i][j] because any smaller value will lead to a smaller square (holes in somewhere). I use maxArea to track the maximal square. When matrix[i][j] == '0', the maximal square ending at position (i, j) is obviously 0.

Let’s consider the following example:

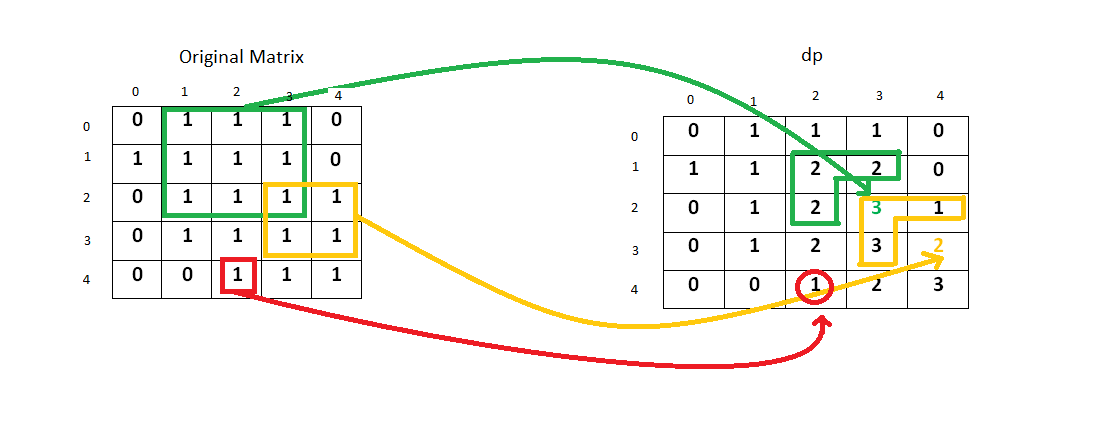
An entry 2 at (i,j) ~ (1,3) implies that we have a square of side 2 up to that index in the original matrix. Similarly, a 2 at (1,2) and (2,2) implies that a square of side 2 exists up to that index in the original matrix. Now to make a square of side 3, only a single entry of 1 is pending at (2,3). So, we enter a 3 corresponding to that position in the DP array.

Elements of Dynamic Programming →

1. Define the problem variable and decide the states: We found that there are two parameters i and j on which state of the problem depends. i and j indicates that dp[i][j] will store the maximum side of the square consisting of 1’s that could be formed while matrix[i][j] be the bottom-most and right-most cell of the square.
2. Define Table Structure and Size: The table structure is defined by the number of problem variables. Since the number of problem variables, in this case, is 2, we can construct a two-dimensional array to store the solution of the sub-problems. Let’s name it dp .
3. Table Initialization: fn(i, j) = int(matrix[i][j]) for i == 0 or j == 0
4. Iterative Structure to fill the table:

• fn(i, j) = 1 + min(fn(i-1, j), fn(i-1, j-1), fn(i, j-1)) if matrix[i][j] == "1"
• fn(i, j) = 0 if matrix[i][j] == "0"

Solution Step

1. Create a DP array of the same size and dimensions as of the input matrix and initialize it with 0.
2. For each element of the matrix, check if it is 1 and then fill the DP array as below

• dp[i][j] = min(dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1]) + 1

3. Return the square of the maximum value of DP array.

Pseudo Code

int maximalSquare( char[][] matrix ) {
    m = matrix.size()
    n = matrix[0].size()
    maxSquareLen = 0
    int[m][n] dp
    for( int i=1 to i <= m) {
        for( int j=1 to j <= n) {
           if( matrix[i-1][j-1] == '1')
                dp[i][j] = min( dp[i-1][j], dp[i][j-1], dp[i-1][j-1] ) + 1
            if( dp[i][j] > maxSquareLen ) 
                maxSquareLen = dp[i][j]
        }
    }
    return maxSquareLen*maxSquareLen
}

Complexity Analysis

Time Complexity: O(mn)

Space Complexity: O(mn)

Critical Ideas To Think

• How did we make sure that dp[i][j] will store the longest length of the square which ends at matrix[i][j]? Can you prove the authenticity of this approach using some examples?
• Why we are returning the square of maxSquareLen ?
• How did we derive the recurrence relation?

3. Space Optimized DP

In the previous approach for calculating dp of ith row we were using only the previous element and the (i−1)th row. Therefore, we don’t need a 2D DP-matrix as 1D DP-array will be sufficient for this.

Solution Steps

1. Create a 1-D dp array containing all 0’s.
2. As we scan the elements of the original matrix across a row, we keep on updating the dp array

• dp[j] = min(dp[j−1],dp[j],prev), where prev refers to the old dp[j−1].

3. Update Dp for every row, and repeat the above steps

Pseudo Code

int maximalSquare(char[][] matrix) {
    maxlen = 0
    m = matrix.size()
    n = matrix[0].size()
    int[n+1] dp = {0}
    for(int i = 0 to i < m) {
        int prev = 0
        for(int j = 1 to j <= n) {
            int tmp = dp[j]
            if(matrix[i][j-1] == '1') {
                dp[j] = min(prev, min(dp[j], dp[j-1])) + 1
                maxlen = max(maxlen, dp[j])
            }
            else 
                dp[j] = 0
            prev = tmp
        }
    }
    return maxlen * maxlen
}

Complexity Analysis

Time Complexity: O(mn)

Space Complexity: O(m) (why?)

Critical Ideas To Think

• How we are updating prev?
• Do you think, whatever we were storing in a 2D Dp array for each row in the previous approach is storing the exact value in a 1D Dp array in this approach with the only difference that it is updating the same 1D Dp array again and again for each row?
• Does this approach have the same elements of dynamic programming than the previous approach? If something has changed, then can you point it out?

Comparison Of Different Approaches

Suggested Problems to Solve

• The maximum rectangular area in a histogram
• Maximal Rectangle of 1’s in a binary matrix
• Largest Plus sign

If you have any more approaches or you find an error/bug in the above solutions, please comment down below.

Happy Coding! Enjoy Algorithms!