Matrix Chain Multiplication

Difficulty: Hard

Asked in: Amazon, Microsoft

Problem Description

Given a chain <M1, M2...Mn> of n two-dimensional matrices, write a program to fully parenthesize the product M1×M2×⋯×Mn in a way that minimizes the number of multiplications.

Problem Note:

• Input: Array of integers M representing a chain of 2-D matrices such that the dimensions of the i-th matrix is M[i-1] x M[i]. Find the most efficient way to multiply these matrices together.
• Output: Return the minimum number of multiplications needed to multiply the chain.
• The problem is not actually to perform the multiplications,
  but merely to decide in which order to perform the multiplications.
• Assume that the matrix dimensions allow multiplication, in order
• Matrix multiplication is associative: M1 (M2M3) = (M1M2) M3

Example 1

Input: M[] = [10, 20, 30, 40, 30]
Output: 30000
Explanation:
Dimensions of M1 = 10 x 20
Dimensions of M2 = 20 x 30
Dimensions of M3 = 30 x 40
Dimensions of M4 = 40 x 30
First, multiply M1 and M2,cost = 10*20*30 = 6000
Second, multilpy (Matrix obtained after multilying M1 and M2) and M3 =  10 * 30 * 40 = 12000
Third, multiply (Matrix obtained after multiplying M1, M2 and M3) and M4 =  10 * 40 * 30 = 12000
Total Cost = 6000 + 12000 + 12000 = 30000

Example 2

Input: M[] = [10, 20, 30] 
Output: 6000
Explanation: There are only two matrices of dimensions 10x20 and 20x30.So there is only one way to multiply the matrices, cost of which is 10*20*30.

Understanding the problem

Given a chain of matrices, we want to multiply them. We cannot change the order of the matrices as that would change the result or make it incompatible, therefore we say matrix multiplication is not commutative.

In addition, regardless of how you parenthesize (e.g. whether the sequence as multiplied as A.(B.C) or (A.B).C ) the chain will give you the same answer, thus we say it is associative.

How we parenthesize the matrices also determines how many operations will be performed. For a multiplication chain of integers, parenthesizing them does not affect the number of operations performed, but for matrices the change is significant.

For example, given the matrices with the following dimensions:

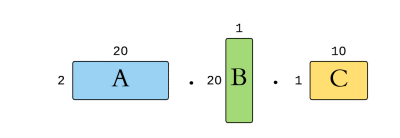
If we define a row of a matrix A as rA and the column as cA , then the total number of multiplications required to multiply A and B is rA.cA.cB.

• A.(B.C) = 2*20*1 + 2*1*10 = 60 multiplications
• (A.B).C = 20*1*10 + 2*20*10 = 600 multiplications

Solution

We will be discussing two solutions for the problem

1. Recursive Solution
2. Dynamic Programming

You may try to solve the problem here.

1. Recursive Solution

To find the minimum number of operations needed to multiply the matrices, we need to derive some formula. Each matrix can only multiply with its adjacent matrix, a prefix can only start from A1 to some matrix Ak, and a suffix can only start from A(k+1) to An, split at some index k.

The resultant dimensions from multiplying 2 matrices are important to find the cost. In a sequence of matrices Ai . . . Aj If we split at a point k, the resultant dimensions of the prefix is ri * ck and the suffix is r(k+1) * cj. The cost of multiplying these 2 matrices are therefore ri * ck * cj .

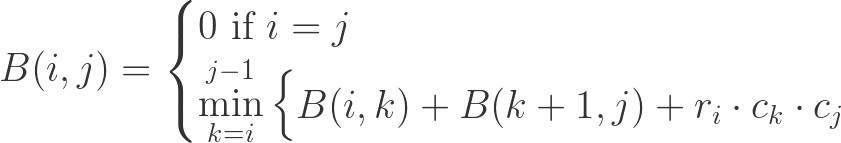
Base case: When there is only 1 matrix. Then the prefix will be equal to the suffix, and there are no operations performed, so the cost would be 0.

Suppose we have a function B(i, j) that computes the minimum number of required operations for multiplying a chain of matrices from matrix i to matrix j. So in a range i to j, we select from j — i possibilities, from i until j — 1. Those possibilities in turn call B recursively until it hits the base case where i = j. We can thus derive the general solution img4 recursion formula

Solution Steps

1. Create a recursive function B, where B(i, j) returns the minimum number of operations for multiplying chain of matrices from i to j.

2. For each i and j, find k between i and j with the minimum cost of multiplication.

Pseudo Code

// recursive utility function
int B(int p[], int i, int j) 
{
    if(i == j) 
        return 0
    int min = INT_MAX
    int count
    for (int k = i to k < j) { 
        count = B(p, i, k) + 
                B(p, k + 1, j) + 
                p[i - 1] * p[k] * p[j]

       if (count < min) 
            min = count
    }
    return min
}
int matrixChainMultiplication(int[] p) {
    return B(p, 1, p.size()-1)
}

Complexity Analysis

Time Complexity: O(2^n)

Space Complexity: O(n)

Critical Ideas to Think

• Why did we divide all the matrices into 3 parts?
• When i == j (base case) then the function returns 0. Why?
• Why are we adding B(p, i, k), B(p, k + 1, j) and p[i — 1] * p[k] * p[j] for the minimum cost of multiplication?
• What does B(i, j) represent here?

2. Dynamic Programming

If we draw the recursion tree for an array of length 4, we could find there are many overlapping subproblems.

The main problem has been broken down into small recurring subproblems (Overlapping Subproblems), which we can piece together to solve the main problem (Optimal Substructure).

1. Define the problem variable and decide the states: Looking at the function B, we will find that there are two parameters i and j on which the state of the problem depends.

2. Define Table Structure and Size: To store the solution of smaller sub-problems in the bottom-up approach, we need to define the table structure and table size.

• The table structure is defined by the number of problem variables. Since the number of problem variables, in this case, is 2, we can construct a two-dimensional array to store the solution of the sub-problems.

3. Table Initialization: We can initialize the table by using the base cases from the recursion.

• the base case is when i = j, then B(i, j) = 0.
• i cannot exceed j, so those areas will need to be greyed out.

4. Iterative Structure to fill the table: We can define the iterative structure to fill the table by using the recurrence relation of the recursive solution.

B(i, j) = B(i, k) + B(k + 1, j) + p[i - 1] * p[k] * p[j]
where k is between i and j

Let's look at the possibilities for an array of length 6.

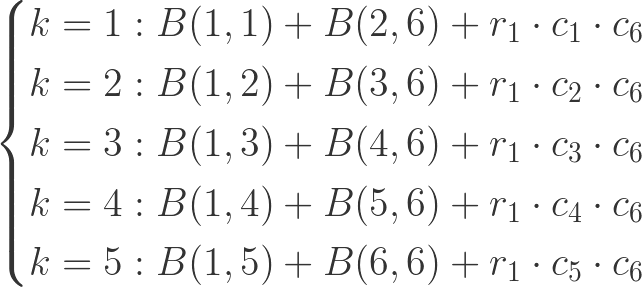
Solution Step

• Create a 2D Dp array.
• Fill DP array in a bottom-up manner as discussed above.
• return DP[1][n] as the least cost.

Pseudo Code

int matrixChainMultiplication(int[] p) {
    int c = p.size()
    int n = c - 1
    int[n][n] DP
    for (int w = n to w > 0) {
        int q = n - w
        for (int j = n to j > q) {
            int i = j - q - 1
            DP[i][j] = INT_MAX
            for (int k = i to k < j) {
                DP[i][j] = min(DP[i][j], DP[i][k] + DP[k + 1][j]
                    + p[i] * p[k + 1] * p[j + 1])
            }
        }
    }
    return DP[1][n]
}

Complexity Analysis

Time Complexity: O(n³)

Space Complexity: O(n²)

Critical Ideas to Think

• Why did we use a 2D-Dp array?
• How the result is stored in DP[1][n] ?
• Do you think that there would not be any value in the lower triangle of DP because i cannot exceed than j?
• Can you dry run the algorithm for an example p and check how does the DP array is storing the results?

Comparison of Different Solutions

Suggested Problems to Solve

• Program for scalar multiplication of a matrix
• Implement Strassen’s Matrix Multiplication Algorithm
• Maximum Length Chain of Pairs
• Tiling Problem

If you have any more approaches or you find an error/bug in the above solutions, please comment down below.

Happy Coding! Enjoy Algorithms!