Longest Increasing Subsequence - Interview Problem

Level: Medium

Asked In: Amazon, Facebook, Microsoft

Understanding the Problem

Problem Description: A subsequence is derived from an array by deleting a few of its elements and not changing the order of remaining elements. You are given an array A with N elements, write a program to find the longest increasing subsequence in the array.

An increasing subsequence is a subsequence with its elements in increasing order. You need to find the length of the longest increasing subsequence that can be derived from the given array.

For example:

Input: A = {3, 10, 2, 1, 20}

Output: 3

Explanation: The longest increasing subsequence is {3,10,20}.

Input: A = {10, 2, 5, 3, 7, 101, 18}

Output: 4

Explanation: The longest incresing subsequence is {2,3,7,101} or {2,3,7,18} or {2,5,7,101} or {2,5,7,18}.

Possible questions to ask the interviewer →

• Can there be duplicate values present in the subsequence? (Ans: We need a strictly increasing sequence. So, No!)
• Am I expected to store the subsequence? (Ans: We require just the length of the longest increasing subsequence, not its elements)

Solutions

We will be discussing 4 possible solutions to solve this problem:-

1. Recursive Approach(Brute Force): We will find the longest increasing subsequence ending at each element and find the longest subsequence.
2. Dynamic Programming Approach: We can improve the efficiency of the recursive approach by using the bottom-up approach of the dynamic programming
3. Greedy Approach: We will use a variant of Patience sorting to get the maximum length of the longest increasing subsequence
4. Greedy + Binary Search: A variation of the above approach to improve the time complexity

1. Recursive Approach(Brute Force)

Let’s try to learn by taking an example.

arr[] = {10, 2, 5, 3, 7, 101, 18}

Thinking of extracting a subsequence by code may be hard because it can start anywhere, end anywhere and skip any number of elements. Let us fix one of these factors then. For each element, we will find the length of the Longest Increasing Subsequence(LIS) that ends at that element.

This way, we have fixed our ending point. Now that we have established the last element of the subsequence, what next? We will proceed recursively. What are the possible second-last elements of the subsequence? All elements with value lesser than the current element that appears on the left of current element, right?

That’s it right there! That’s the basis of our recurrence relation.

lis_ending_here(arr, i) = 1 + lis_ending_here(arr, j)

--> j < i and arr[j] < arr[i]

If we do this for each element, we will have our answer.

Solution Steps

We will need to use a helper function to ease our implementation.

1. Declare and initialize a variable max_ans with 1, because a single element is a subsequence too of length 1.
2. For each index from 0 to N-1, find the maximum LIS ending at that index using our helper function lis_ending_here().
3. The helper function accepts the array and curr index. We need to find the LIS ending at curr.
4. The base case here is curr == 0. Only a subsequence of length is possible at this point consisting of the first element itself.
5. For the recursion, iterate from curr-1 to index 0 and for all elements less than current element, recursively call this helper function and update ans as per need.

Pseudo-Code

int lis_ending_here(int arr[], int curr)
{
    // Only one subsequence ends at first index, the number itself
    if(curr == 0)
        return 1

    int ans = 1
    for(i = curr-1 to 0, decrement of -1)
        if(arr[i] < arr[curr])
            ans = max(ans, 1 + lis_ending_here(arr, i))
    return ans
}

int longest_increasing_subsequence(int arr[], int N)
{
    // Because a single number can be a subsequence too
    int max_ans = 1

    for(i = 0 to N-1)
        max_ans = max(max_ans, lis_ending_here(arr, i))

    return max_ans
}

Complexity Analysis

Recurrence relation: T(N) = 1 + Sum j = 1 to N-1 (T(j))

Time Complexity: O(2^N) (Think!)

Space Complexity: O(N), for stack space in recursion

Critical ideas to think!

• Is this recursion top-down or bottom-up?
• Can you see the overlapping subproblems in this case?
• What’s the order of elements in the array that is the worst-case for this problem?
• To confirm the space complexity in recursion, draw the recursion tree. The height of the tree is the stack space used.

2. Dynamic Programming Approach

Create a recursion tree for the above recursion.

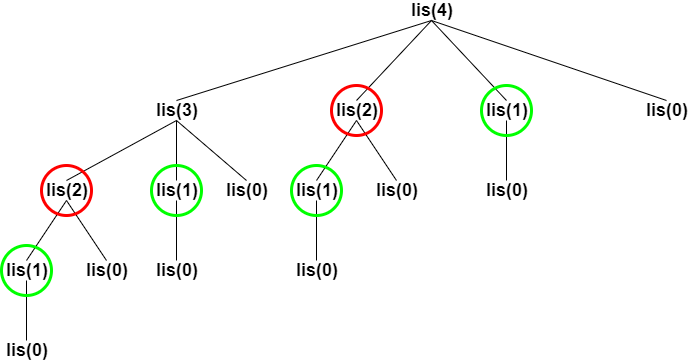
As you can clearly see in the recursion tree, there are overlapping subproblems and also holds an optimal substructure property. This means we could improve the time complexity of our algorithm using Dynamic Programming.

Elements of Dynamic Programming

Well, the recursion approach above is top-down. This means the implementation of our dynamic programming should be bottom-up. What are the other elements of dynamic programming we need to figure out?

1. Define problem variables and decide the states: There is only one parameter on which the state of the problem depends i.e. which is N here, the size of the array.

2. Define Table Structure and Size: To store the solution of smaller sub-problems in bottom-up approach, we need to define the table structure and table size.

• The table structure is defined by the number of problem variables. Since the number of problem variables, in this case, is 1, we can construct a one-dimensional array to store the solution of the sub-problems.
• The size of this table is defined by the number of subproblems. There are total N subproblems, each index forms a subproblem of finding the longest increasing subsequence at that index.

3. Table Initialization: We can initialize the table by using the base cases from the recursion. (Think)

• lis[0] = 1

4. Iterative Structure to fill the table: We can define the iterative structure to fill the table by using the recurrence relation of the recursive solution.

lis[i] = lis[j] + 1

--> j < i and arr[j] < arr[i]

5. Termination and returning final solution: After filling the table in a bottom-up manner, we have the longest increasing subsequence ending at each index. Iterate the auxiliary array to find the maximum number. It will be the longest increasing subsequence for the entire array

Solution Steps

1. Create a 1D array lis[] of size N.
2. Iterate for each element from index 1 to N-1.
3. For each element, iterate elements with indexes lesser than current element in a nested loop
4. In the nested loop, if the element’s value is less than the current element, assign lis[i] with (lis[j]+1) if (lis[j]+1) is greater than lis[i].
5. Traverse the entire lis[] array to extract the maximum element which will be our answer.

Pseudo-Code

int longest_increasing_subsequence(int arr[], int N)
{
    int lis[N]
    for(i = 0 to N-1)
        lis[i] = 0
    lis[0] = 1
    for(i = 1 to N-1)
    {
        for(j = 0 to i-1)
        {
            if(arr[j] < arr[i])
                lis[i] = max(lis[i], lis[j] + 1)
        }
    }
    int ans = 1
    for(i = 0 to N-1)
        ans = max(ans, lis[i])
    return ans
}

Complexity Analysis

For each element, we traverse all elements on the left of it.

Time Complexity: O(N²)(Think!)

Space Complexity: O(N), for storing the auxiliary array

Critical ideas to think!

• Can you recover the subsequence with maximum length by modifying this algorithm?
• Can you find all subsequences of maximum length in the array?

3. Greedy Approach

There also exists a greedy approach to this problem. But how can a problem have both dynamic and greedy approaches? Of course, it's possible. Dynamic Programming was chosen just because there were overlapping subproblems and optimal substructure. This doesn’t mean a greedy approach is not possible.

We will use a variant of patience sorting to achieve our goal. But what is patience sorting? Well, let us try to understand this approach by visualizing an example using a deck of cards.

→ Assume you have a certain permutation of a deck of cards with all cards face up in front of you. Your task is to divide the cards into piles:-

1. A card with a lower value may be placed on a card with a higher value. You can only see the top card of each pile. This way each pile is in increasing order from top to bottom.
2. If no piles have the topmost card with a value higher than the current value, you may start a new pile placed at the rightmost position of current piles.

Now let’s start placing cards in piles…

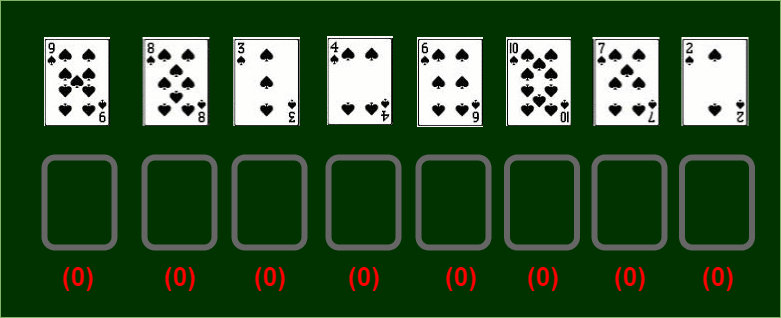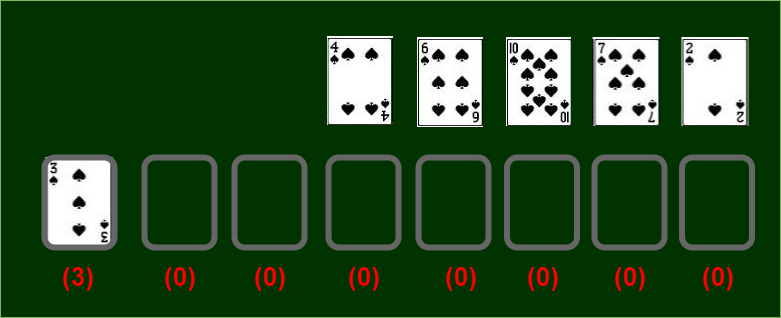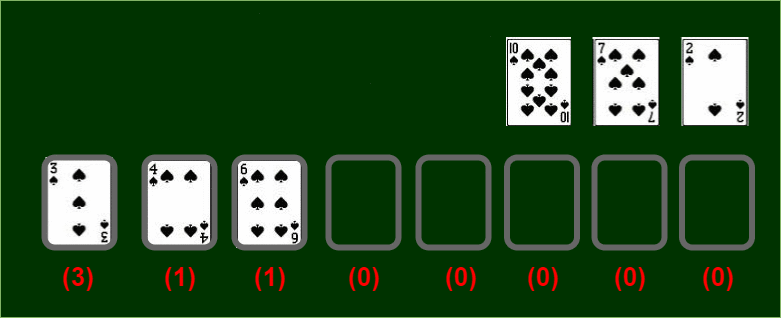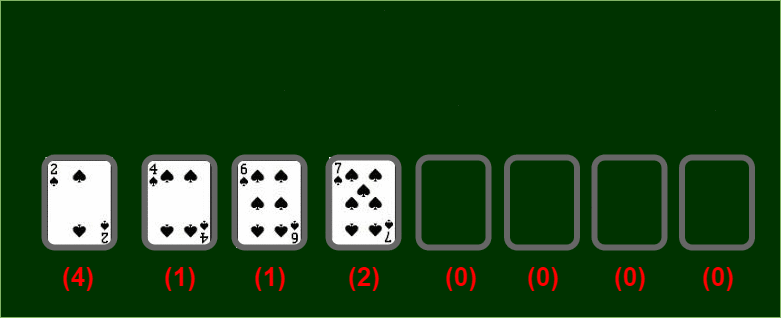
Patience Sorting involves merging these k-sorted piles optimally to obtain the sorted list. But our objective is attained in the first phase of this algorithm. Didn’t you notice?

The pile with the most number of cards is our longest increasing subsequence. Easy, right? You can do the same when you’re given a list of numbers.

How will you implement it? (Think!)

Solution Steps

Our algorithm is divided into two phases, select the first pile suited to place the number in and then place the element in that pile.

1. Create two arrays pile_top[] and pile_length[] of length N, because there can be a maximum number of N piles.
2. The pile_top[] array must be initialized with INT_MAX and pile_length[] with 0. Why is pile_top[] initialized with INT_MAX? Think!
3. For each element, traverse pile_top[] to find the first pile that has the top value greater than the current element, increase the pile_length[] at that index by 1 and change value at pile_top[] with the current element.
4. Traverse the pile_length[] array and find the maximum value in it.
5. The maximum value is the length of longest increasing subsequence in the array.

Pseudo-Code

int longest_increasing_subsequence(int arr[], int N)
{
    int pile_top[N], pile_length[N]

    for( i = 0 to N )
        pile_top[i] = INT_MAX
    for( i = 0 to N )
        pile_length[i] = 0

    for( i = 0 to N )
    {
        for( j = 0 to N )
        {
            if(pile_top[j] > arr[i])
            {
                pile_top[j] = arr[i]
                pile_length[j] += 1
                break
            }
        }
    }

    int ans = 0
    for( i = 0 to N )
        ans = max(ans, pile_length[i])
    
     return ans
}

Complexity Analysis

For each element in the array, we select the first pile that has the top element higher than the current element. The number of piles can be maximum up to length N. So there are N elements in the array and for each of them, we need to search another list of maximum length N.

Time Complexity: O(N) * O(N) = O(N²) (Why?)

Space Complexity: O(N) + O(N) = O(N), for storing two arrays

Critical ideas to think!

• What happens in this approach in case of the presence of duplicate values in the array?
• Can you improve the time complexity for selecting the correct pile to put the element into? (Hint: Print the array, notice anything special about the array that will help us search a lot faster?)

4. Greedy Approach + Binary Search

As the title must’ve hinted you by now, we will use Binary Search to select the pile. But isn’t it true that binary search can only be applied to sorted arrays? Yeah, so? Notice that the pile_top[] array is sorted in nature. (Print the array if you feel so, to check!).

Basically, our purpose in the searching phase is → We are given a sorted array and we need to find the first number in the array that is greater than the current element.(Try to understand how our problem got reduced to this problem).

Conclusion: We now need to find the upper bound of each element in the pile_top[] array.

Its sometimes easier and faster to solve a problem by trying to divide it into smaller subproblems and solving them individually and optimally.

So now we need to find the upper bound of the given number in the array. Upper bound can be found in O(logn) using a variation of binary search.

Solution Steps

The solution steps for this algorithm are quite similar to the one stated in the previous approach, except for the searching phase. We will find the upper bound of the array elements in the pile_top[] array. Let us discuss the steps to find the upper bound of a given element in an array.

Given array = arr[], given element = item

1. Set low = 0 and high = arr.length() -1.
2. Start a while loop until low < high
3. Initialize mid = (low+high)/2.

• If arr[mid] ≤ item, the upper bound lies on the right side. low = mid+1.
• Else, high = mid.

4. Return low

Pseudo-Code

int upper_bound(int arr[], int item)
{
    int low = 0, high = arr.length()-1 
    
    while(low <= high)
    {
        int mid = (low + high)/2
        if(arr[mid] <= item)
            low = mid+1
        else
            high = mid
    }
    return low
}

int longest_increasing_subsequence(int arr[], int N)
{
    int pile_top[N], pile_length[N]

    for( i = 0 to N )
        pile_top[i] = INT_MAX
    for( i = 0 to N )
        pile_length[i] = 0

    for( i = 0 to N )
    {
        int j = upper_bound(pile_length, arr[i])
        pile_top[j] = arr[i]
        pile_length[j] += 1
    }

    int ans = 0
    for( i = 0 to N )
        ans = max(ans, pile_length[i])
    
    return ans
}

Complexity Analysis

Time Complexity: Find upper bound for each element in the array = O(N) * O(logn) = O(Nlogn)

Space Complexity: O(N) + O(N) = O(N), for storing the two auxiliary arrays

Critical ideas to think!

• What are some other problems that can be solved using both dynamic programming and greedy approach?
• How does this algorithm perform with duplicate values in the array?
• How would you find the longest non-decreasing sequence in the array?

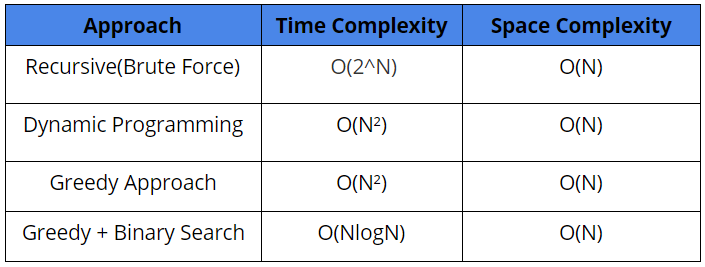
Comparison between different solutions

Suggested Problems to solve

• Find the longest common subsequence in the given two arrays
• Find the longest strictly decreasing subsequence in an array
• Find the longest non-decreasing subsequence in an array
• Find the length of longest subsequence in arithmetic progression
• Find the longest bitonic subsequence in an array

Happy Coding!

Team AfterAcademy 🙂