What is the two pointer technique?

What is the Two pointer technique?

Concept Introduction

Two pointer approach is an essential part of a programmer’s toolkit, especially in technical interviews. The name does justice in this case, it involves using two pointers to save time and space. (Here, pointers are basically array indexes).

Just like Binary Search is an optimization on the number of trials needed to achieve the result, this approach is used for the same benefit.

The idea here is to iterate two different parts of the array simultaneously to get the answer faster.

Implementation

There are primarily two ways of implementing the two-pointer technique:

1. One pointer at each end

One pointer starts from beginning and other from the end and they proceed towards each other

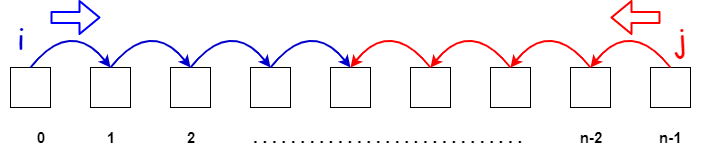
Example : In a sorted array, find if a pair exists with a given sum S

Brute Force Approach: We could implement a nested loop finding all possible pairs of elements and adding them.

bool pairExists(int arr[], int n, int S)
{
    for(i = 0 to n-2)
        for(j = i+1 to n-1)
            if(arr[i] + arr[j] == S)
                return true
    return false
}

Time complexity: O(n²)

Efficient Approach

bool pairExists(int arr[], int n, int S)
{
    i = 0
    j = n-1
    while( i < j)
    {
        curr_sum = arr[i] + arr[j]
        if ( curr_sum == S)
            return true
        else if ( curr_sum < X )
            i = i + 1
        else if ( curr_sum > X )
            j = j - 1
    }
    return false
}

Time Complexity: O(n)

2. Different Paces

Both pointers start from the beginning but one pointer moves at a faster pace than the other one.

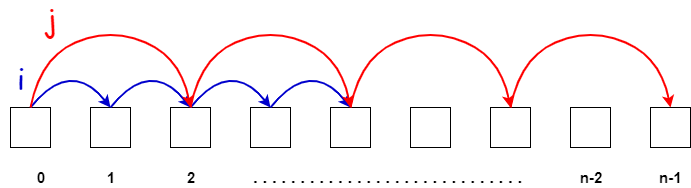
Example: Find the middle of a linked list

Brute Force Approach: We can find the length of the entire linked list in one complete iteration and then iterate till half-length again.

ListNode getMiddle(ListNode head)
{
    len = 0
    ListNode curr = head
    while ( curr != NULL )
    {
        curr = curr.next
        len = len + 1
    }
    
    curr = head
    i = 0
    while(i != len / 2)
    {
        curr = curr.next
        i = i + 1
    }
    return curr
}

Efficient Approach: Using a two-pointer technique allows us to get the result in one complete iteration

ListNode getMiddle(ListNode head)
{
    ListNode slow = head
    ListNode fast = head
   while(fast && fast.next)
    {
        slow = slow.next
        fast = fast.next.next
    }
   return slow
}

How does this technique save space?

There are several situations when a naive implementation of a problem requires additional space thereby increasing the space complexity of the solution. Two-pointer technique often helps to decrease the required space or remove the need for it altogether

Example: Reverse an array

Naive Solution: Using a temporary array and fillings elements in it from the end

int[] reverseArray(int arr[], int n)
{
    int reverse[n]
   for ( i = 0 to n-1 )
        reverse[n-i-1] = arr[i]
    
    return reverse
}

Space Complexity: O(n)

Efficient Solution: Moving pointers towards each other from both ends and swapping elements at their positions

int[] reverseArray(int arr[], int n)
{
    i = 0
    j = n-1
   while ( i < j )
    {
        swap(arr[i], arr[j])
        i = i + 1
        j = j - 1
    }
   return arr
}

Space Complexity: O(1)

Some popular examples of two pointer approach

Pseudo code: Merge two sorted array

void mergeSortedArrays(int A[], int B[], int n1, 
                             int n2, int C[]) 
{ 
    int i = 0, j = 0, k = 0
    while (i<n1 && j <n2) 
    { 
        if (A[i] < B[j]) 
        {
            C[k] = A[i]
            k = k + 1
            i = i + 1
        }    
        else
        {
            C[k] = B[j]
            k = k + 1
            j = j + 1
        }    
    }
    while (i < n1) 
    {
        C[k] = A[i]
        k = k + 1
        i = i + 1
    }    
    while (j < n2) 
    {
        C[k] = B[j]
        k = k + 1 
        j = j + 1
    } 
}

Both pointers are moving forward in the same direction and each step of iteration we are moving one pointer forward. Time Complexity = O(n1 + n2) (Think!)

Pseudo code: Partition function in quick sort

int partition (int A[], int l, int r)  
{  
    int pivot = A[r]
    int i = l - 1
    for (j = l to r-1)  
    {  
        if (A[j] < pivot)  
        {  
            i++ 
            swap(A[i], A[j]) 
        }  
    }  
    swap(A[i + 1], A[r])
    return (i + 1)
}

Both pointers are moving forward in the same direction with different pace i.e. j is incrementing by 1 after each iteration but i is incrementing if (A[j] < pivot). Time complexity = O(n) (Think!)