Missing Number

Difficulty: Easy

Asked in: Amazon, Yahoo

Understanding The Problem

Problem Description

Given an array arr[] consists of 0, 1, 2, 3, 4,..... n . But one of the numbers is missing in it. Write a program to find the number that is missing from the array.

Problem Note: Your algorithm should run in linear runtime complexity. Could you implement it using only constant extra space complexity?

NOTE: All the elements in the array are distinct.

There will be only one missing number in the given array, two missing numbers will not be there. Also, if there is no missing number then you have to return the number that is coming just after the largest element of the array.

Example 1

Input: arr[] = [4,3,1,2]
Output: 0
Explanation: The array should have elements 0,1,2,3,4 but 0 is missing. So, the answer is 0.

Example 2

Input: arr[] = [4,5,0,6,1,7,3]
Output: 2
Explanation: All the numbers except 2 are present in the given array consisting of 0,1,2..7

Example 3

Input: arr[] = [4,3,1,0,2]
Output: 5
Explanation: All distinct elements 0,1,2,3,4,5 should be present in the array but 5 is missing. So, the answer is 5.

Solutions

We will be discussing three solutions for the problem

Sorting: Sort the array and compare each index with the value at that index, if it's not equal then return the index
Hashing: Store the values of the array in a hashmap and iterate over the range from 0 to n.
Sum of n whole numbers: Find the sum of n numbers and the sum of the array and return the difference between them.

You may try this problem here now .

1. Sorting

To find the missing number in the range of size of the array, we can easily sort the array knowing that the values in the array are in the range of size of the array and they are not duplicate.

So, If we sort the array, then we can conclude that the first number not matching with its index value is our missing number.

Solution Steps

Sort the input array
iterate over the array until arr[idx] == idx otherwise, return idx as the answer.

Pseudo Code

int getMissingNumber(int[] arr) {
     arr.sort()
     size = arr.length
     for(i = 0 to i < size){
         if(arr[i] != i){
             return i
         }
     }
     return i+1
}

Complexity Analysis

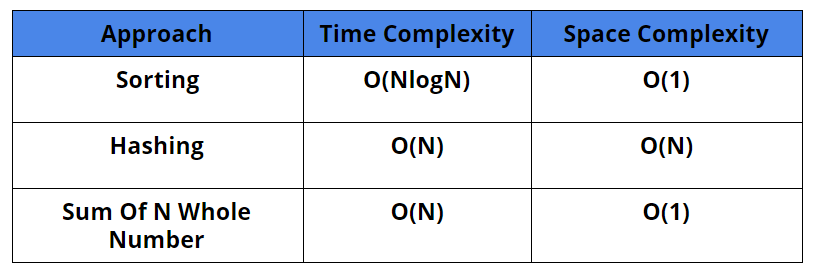
Time Complexity: O(NlogN)

Space Complexity: O(1)

Critical Ideas to Think

Why are we comparing arr[i] with i ?
Why did we return i+1 in the end?
Can you optimize the time complexity?

2. Hashing

We can create a set or hashmap to store each value inside it knowing that search operation inside a set or hashmap is O(1). Now if we iterate over the range from 0 to the size of the array, then we can look for each value whether or not they are present inside the set. The first number not found in the set will be our answer.

Solution Steps

Create a hashmap and store all the value inside it
Now iterate over the range from 0 to size of the array

Return the first element not present inside the set or hashmap.

Pseudo Code

int getMissingNumber(int[] arr) {
    size = arr.length
    set = Set()
    for(i = 0 to i < size) {
        set.add(arr[i])
    }
    for(i = 0 to i <= size) {
        if(i not in set){
            return i
        }
    }
}

Complexity Analysis

Time Complexity: O(n)

Space Complexity: O(n)

Critical Ideas to Think

Why did we iterate till i<=size in the second for loop?
Give reasons why will this approach work!
Can you optimize the space complexity?

3. Sum of N Whole Numbers

We know that the missing number is in the range from 0 to N (including 0 and N). Let p be a number missing in the sum of range from 0 to N, then the total sum would be sigma(0 to N)-p . Where sigma(0 to N) is N*(N+1)/2 .

So, we can deduce that the difference of the sum of N whole numbers and the sum of the array will be the missing number.

Consider example 2,

arr_sum = 4+5+0+6+1+7+3 =26
expected_sum = 7*8/2 = 7*4 = 28
So, missing number = 28-26 = 2

Solution Steps

Store the sum of the array in arr_sum
Store the sum of N whole numbers in exp_sum where N is the length of the array.
Return the difference between exp_sum and arr_sum .

Pseudo Code

int getMissingNumber(int[] arr) {
    size = arr.length
    arr_sum = 0
    for(i = 0 to i < size) {
        arr_sum = arr_sum + arr[i]
    }
    exp_sum = size * (size+1) / 2
    return exp_sum - arr_sum
}

Complexity Analysis

Time Complexity: O(n)

Space Complexity: O(1)

Critical Ideas To Think