Find Nth Factorial

Difficulty: Easy

Understanding The Problem

Problem Description

Write a program to find the factorial of a given number n .

Problem Note

n is a non-negative integer.
Factorial of a non-negative integer n is the multiplication of all integers smaller than or equal to n

Example

Input: n = 6
Output: 720
Explanation: Factorial of 6 is 6*5*4*3*2*1 which is 720.

Solution

Recursive Solution : For f(x), return 1 when x is 0 , otherwise return x*f(x-1)
Iterative Solution : Iterate from 1 to x and maintain a factorial variable.

You can try the problem here.

1. Recursive Solution

We have to find the factorial of a number. Mathematically, the factorial of a number is the product from 1 to that number.

i.e. factorial(Z) = 1 x 2 x 3 x 4 . . . x (Z-2) x (Z-1) x Z

Looking over the above equation, we can conclude that the factorial(Z) = factorial(Z-1) x Z

Now, the equation seems like a recursive structure, where factorial is a function and we have to find the factorial of Z . Now, We know that the factorial of 0 is 1 and factorial doesn’t exist for -ve numbers. We can use this as a base case of the recursive function.

Base Case

Now think about the base case, where the function will directly give you results without breaking it again into sub-problem.

fact(5) 
= 5 * fact(4) 
= 5 * 4 * fact(3) 
= 5 * 4 * 3 * fact(2) 
= 5 * 4 * 3 * 2 * fact(1) 
= 5 * 4 * 3 * 2 * 1 * fact(0)

The factorial of a negative number is not defined, so fact(0) is the smallest version of the factorial problem where our solution will terminate. Here n = 0 is the base case which will return 1. Since 0! = 1.

To understand more about recursion, refer here .

Solution Steps

Create a recursive function factorial(Z)
Return 1 when Z is 0.
Otherwise, return Z * factorial(Z-1)

Pseudo Code

int findFactorial(int n) {
    if(n is 0)
        return 1
    return n * (findFactorial(n-1))
}

Complexity Analysis

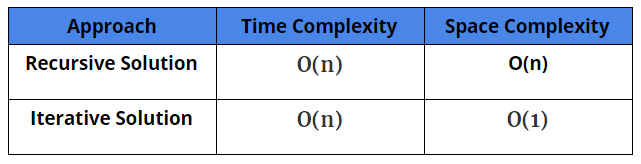
Time Complexity: O(n)

Space Complexity: O(n)

Critical Ideas To Think

How did we define the recursive structure?
Why we returned 1 when n is 1?
Why is the space complexity is of O(n)? Answer : The recursive function uses stack space and in this case, we are recursively calling the function until n reaches to 0 and that will create n stack frames in the memory.
Can you draw the recursion tree for this case?

2. Iterative Solution

Instead of going recursive, we can use the logic of factorial in the way we do it in our notebooks and that is multiplying numbers from 1 to n.

So, the straight forward way is to use a for loop and iterate till n while maintaining a variable that will store the factorial.

Solution Steps

Create a factorial variable and initialize it with 1
Create a for loop and iterate from 1 to n
In each iteration, multiply factorial with i
Return factorial

Pseudo Code

int findFactorial(int n) {
    int factorial = 1
    for(int i = 1 to i <= n){
         factorial = factorial * i
    }
    return factorial
}

Complexity Analysis

Time Complexity: O(n)

Space Complexity: O(1)

Critical Ideas To Think

Why we started the iteration from 1 while the base case in recursive function was n is 0 ?
According to you, what should be the maximum number for which you can find the factorial if you are using a single processor system and using some data structure like Big integer?