Minimum Number Of Jumps To Reach End
AfterAcademy Tech
•
18 Jul 2020

Difficulty: Hard
Asked in: Amazon, Google, Ebay
Understanding The Problem
Problem Description
Given an array of non-negative integers arr[] of length n, where each element represents the max number of steps that can be made forward from that element. You are initially positioned at the first index of the array. Write a program to return the minimum number of jumps to reach the last index of the array.
Problem Note
- If it is not possible to reach the last index, return -1.
- If an element is 0, then you cannot move through that element.
Example 1
Input: arr[] = [2, 1, 1]
Output: 1
Explanation: The minimum number of jumps to reach the last index is 1. Jump 2 steps from index 0 to 2.
Example 2
Input: arr[] = [2, 3, 2, 4, 4]
Output: 2
Explanation: The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
Solutions
- Brute Force Solution → We will start with the ‘0’th index and try all options. After taking a jump to an index, we recursively try all options from that index.
- Dynamic Programming → For each value at the ith index, move from ith index to ith+ar[i] and update the minimum number of jumps till there.
- Optimized Dynamic Programming
You can try to solve the problem here.
1. Brute Force Solution
The most basic approach for the problem is to start from the first element and recursively call for all the elements reachable from the first element.
The minimum number of jumps to reach the end from first can be calculated using the minimum number of jumps needed to reach the end from the elements reachable from first.
minJumps(start, end) = Min ( minJumps(k, end) ) for all k reachable from start.
In other words, from start move to all such indexes that are reachable from start and then recursively get the minimum number of jumps needed to reach the end from these reachable options.
Look at the below example:
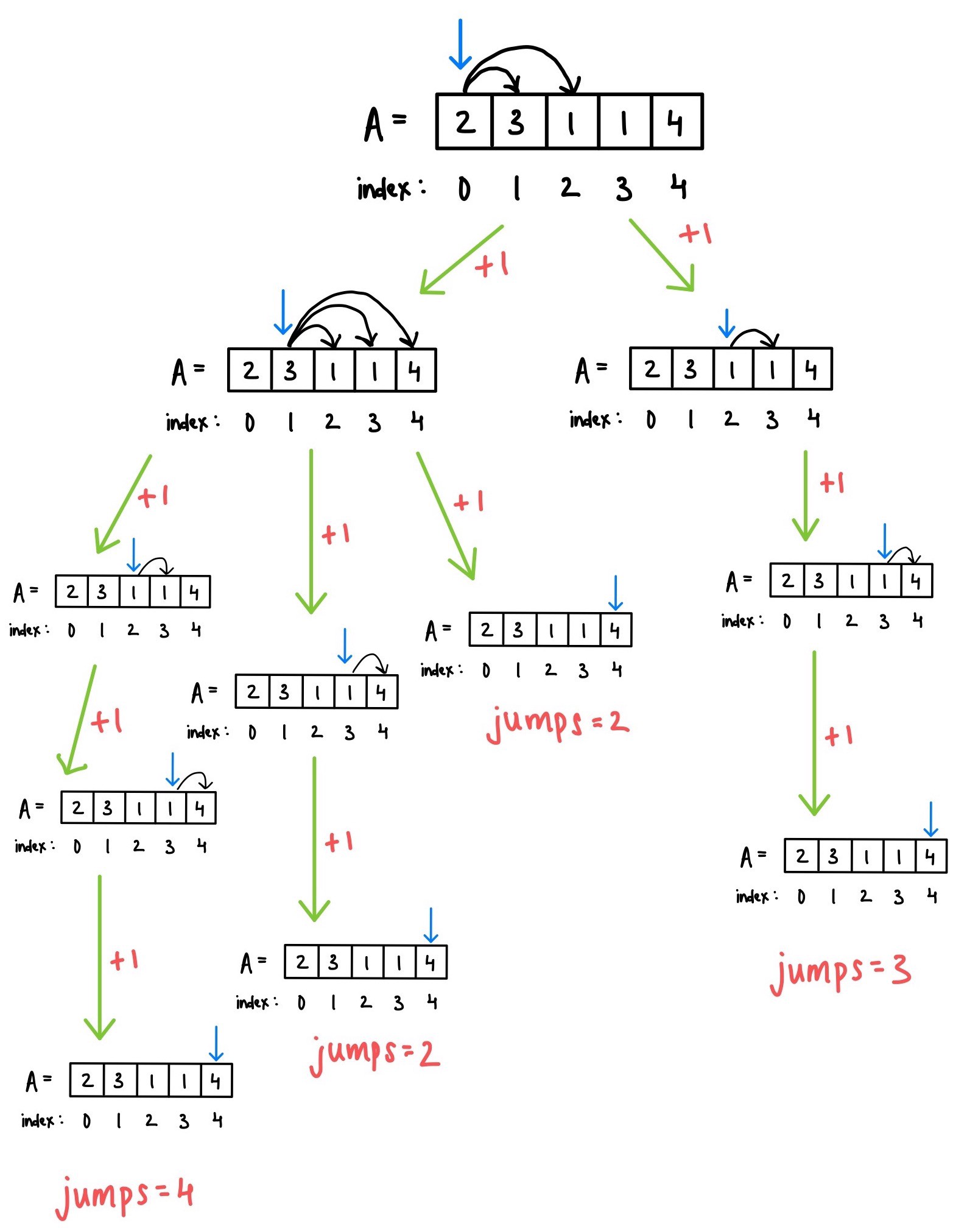
Solution Steps
- Create a recursive function which will return the minimum number of jumps needed to reach from the current position to the end
- a
minJumpwill store the minimum number of jumps as an answer maxStepswill store the maximum number of positions we can move from thecurrPos- Iterate till
maxSteps > 0and for each position, call the recursive function to reach till the end and thereby increment the jumps by 1 for each jump.
Pseudo Code
int decideJump(int[] nums, int n, int currPos){
if(currPos >= n-1){
return 0
}
int minJump = INT_MAX
int maxSteps = nums[currPos]
while(maxSteps > 0){
minJump = min(minJump, 1 + decideJump(nums,n,currPos+maxSteps))
maxSteps = maxSteps - 1
}
return minJump
}
int jump(int[] nums, int n) {
return decideJump(nums, n, 0)
}
Complexity Analysis
Time Complexity: O(n^n)
Space Complexity: O(1), not considering recursion stack space.
Critical Ideas To Think
- What is the recurrence relation for this approach?
- Why did we maintain the maxSteps variable here?
- Why did we initialize minJump with INT_MAX?
2. Dynamic Programming
You must have noticed that we were recalculating the minimum number of steps to reach the end of the brute force approach. If we could remove such recalculations by memorizing the minimum jumps from each index to reach the end will lead to a more optimized solution which is called dynamic programming.
How will we do that?
We will go with the elements of dynamic programming:-
1. Define the problem variable and decide the states: There is only one parameter on which the state of the problem depends i.e. which is N here.
2. Define Table Structure and Size: To store the solution of smaller sub-problems in the bottom-up approach, we need to define the table structure and table size.
- The table structure is defined by the number of problem variables. Since the number of problem variables, in this case, is 1, we can construct a one-dimensional array to store the solution of the sub-problems.
- The size of this table is defined by the number of subproblems. There are a total of N subproblems.
3. Table Initialization: We can initialize the table by using the base cases from the recursion. (Think)
- minJumps[0] = 0
4. Iterative Structure to fill the table: We can define the iterative structure to fill the table by using the recurrence relation of the recursive solution.
minJumps[i] = 1 + min(minJumps[i], 1 +
min( minJumps[i+1],
minJumps[i+2],
. . .
minJumps[i + minJumps[i] + 1]
)
)
5. Termination and returning final solution: After filling the table, our final solution gets stored at the last Index of the array i.e. return minJumps[N-1].
Look at the below example to understand the discussed scenario. The respective colored boxes represent overlapping subproblems.
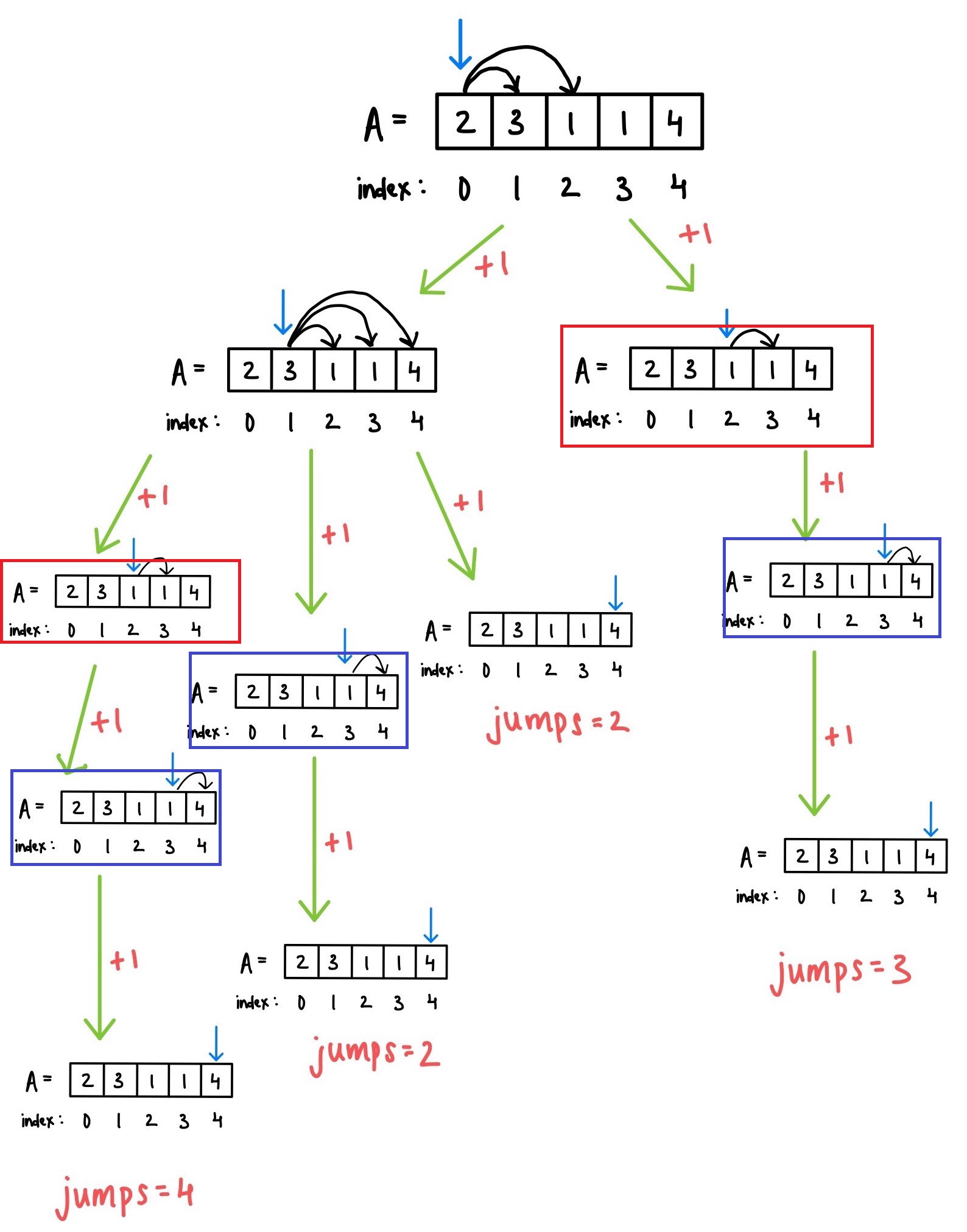
Solution Steps
- Create a dp array
minJumpsof sizento store the minimum number of jumps from ith index to reach the end and initialize it with INT_MAX. - Initialize
minJumps[0] = 0(Why?) - Fill the table by following the iterative structure discussed above.
- Return the last index of
minJumps
Pseudo Code
int minJump(int[] num, int n){
int[n] minJumps = {INT_MAX}
minJumps[0] = 0
for(i = 0 to i < n){
for(j = i+1 to j < min(i+num[i]+1, n)) {
minJumps[j] = min(minJumps[j], 1 + minJumps[i])
}
}
return minJumps[n-1]
}
Complexity Analysis
Time Complexity: O(n²)
Space Complexity: O(n)
Critical Ideas To Think
- What do the elements of dynamic programming mean?
- How did we reach the iterative structure?
- Why did we maintain a 1-D Dp array?
3. Greedy Approach
The difference between greedy and dynamic approach is that the DP solves subproblems first, then uses those solutions to make an optimal choice whereas Greedy makes an optimal choice (without knowing solutions to subproblems) and then solve remaining subproblem(s), but both apply to problems with optimal substructure.
Here, the problem only asks for the min number of jumps. So we do not have to figure out each jump position. We only need to store the max_reach of the previous jump position. If we go beyond that, we need one more jump.
Solution Steps
- Initialize
previous, current, jumpswith0 - for each index
i, check ifiis greater than previous, this means that we cannot go further, so we need to increase the jump and set thepreviousto thecurrent. - for each index
i, updatecurrentwithmax(current, i+nums[i]), wherecurrentrepresents all time the maximal reachable index in the array.
Pseudo Code
int jump(int[] nums, int n) {
int previous = 0
int current = 0
int jumps = 0
for(int i = 0 to i < n) {
if(i > previous) {
jumps = jumps + 1
previous = current
}
current = max(current, i + nums[i])
}
return jumps
}
Complexity Analysis
Time Complexity: O(n)
Space Complexity: O(1)
Critical Ideas To Think
- Why is the following approach called greedy?
- What does previous represent here?
- How are we updating the maximum jumps that could be made from an index i?
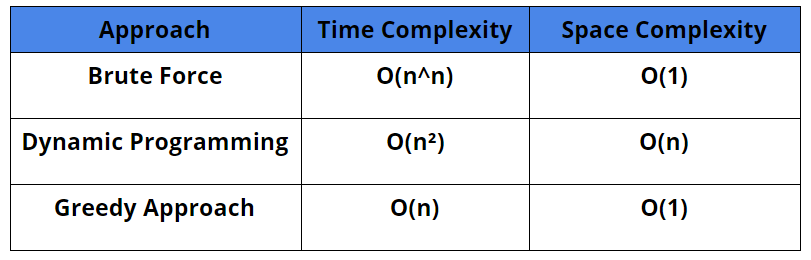
Comparison Of Solutions
Suggested Problems To Solve
- Partition equal subset sum
- Minimum number of moves to reach N starting from (1, 1)
- Find a minimum number of steps to reach the end of String
- Minimum number of moves required to reach the destination by the king in a chessboard
- Find if two people ever meet after the same number of jumps
- Number of jumps for a thief to cross wall
If you have any more approaches or you find an error/bug in the above solutions, please comment down below.
Happy Coding!
Enjoy Algorithms!
Written by AfterAcademy Tech
Share this article and spread the knowledge
Read Similar Articles
AfterAcademy Tech
Minimum Depth of Binary Tree - Interview Problem
Given a binary tree, find its minimum depth. The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

AfterAcademy Tech
Find minimum and maximum value in an array - Interview Problem
Given an array A[] of size n, you need to find the maximum and minimum element present in the array.Your algorithm should make minimum number of comparisons.

AfterAcademy Tech
Missing Number
Given an array arr[] consists of 0, 1, 2, 3, 4,.....n. But one of the numbers is missing in it. Write a program to find the number that is missing from the array.

AfterAcademy Tech
Minimum Spanning Tree
In this blog, we will learn about Minimum Spanning Tree. We will also discuss two algorithms which is used to find a minimum spanning tree.
