Letter Combinations of a Phone Number

Difficulty: Hard

Asked in: Google

Understanding The Problem

Problem Description

Given a string str , containing digits from 2 - 9 inclusive, write a program to return all the possible letter combinations that the number could represent.

Problem Note:

Your answer could be in any order you want.
A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.

Example

Input: "24" 
Output: ["ag","ah","ai","bg","bh","bi","cg","ch","ci"]

Solution

The problem statement explains that we have to generate all the possible combinations of characters that can be obtained from the respective digit of the phone’s keypad. Looking over the given example,

2 can generate “a” or “b” or “c”
4 can generate “g” or “h” or “i”
We can take one character from each of the digits to form a string. All such possible combinations of characters will generate all the strings which will be our required answer.

But, How will we do that?

You can try to think of a recursive approach as it is very intuitive, where at each stage of recursion there will be a digit that will offer the respective set of characters, and then we will recursively send the next digit to look for those set of characters that could be appended in our result string.

Look at the below recursion tree for the above example.

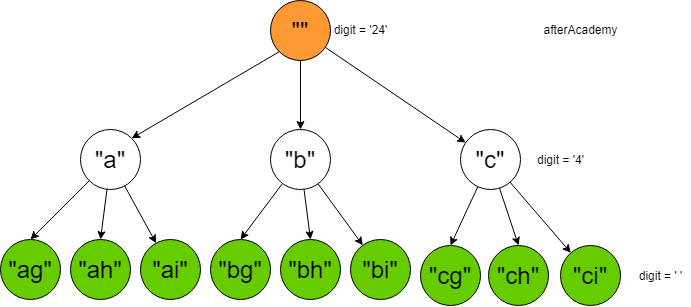
The green circles show the base case for the recursion when the length of the string is equal to the length of input digits.

What if we have more than 2 digits as input?

In that case, the recursion tree will have further children until the result string length will be equal to the number of input digit (Why?) .

In short, We keep adding each possible letter recursively and this will generate all the possible strings.

Is there an iterative solution to this problem?

Generally, we can convert all-recursive solution to an iterative solution. Here, if we look at the recursion tree, you can draw conclusions that to get all possible strings, we can make a DFS search or a BFS search. If we use the DFS approach then we can use stack and if we use BFS then we can use a queue. However, the answer would be the same in both the iterative approach.

If we will use the BFS approach, then we can take a queue of strings and will push an empty string to it. For all the corresponding keypad characters of the input digit, we will be appending those characters to the front of the queue and then pushing them into the queue until the length of strings in the queue becomes equal to the length of the input digit string.

You can practice this problem here.

Solution Steps

Create a recursive function recurse(combination, next_digits)
Add a base case: If there are no more digits to check that means that the current combination is done.
If there are still digits to check :

Iterate over the letters mapping the next available digit.
Append the current letter to the current combination combination = combination + letter .
Proceed to check the next digits : recurse(combination + letter, next_digits[1:]) .

Pseudo Code

Backtracking / Recursive Approach

string[] KEYS = { "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" }

// driver function
string[] letterCombinations(String digits) {
    string[] res
    combination("", digits, 0, res)
    return res
}
// recursive function
void combination(string prefix, String digits, int idx, string[] res) {
    if (idx >= digits.length()) {
        res.add(prefix)
        return
    }
    string letters = KEYS[int(digits[idx])]
    for (int i = 0 to i < letters.length()) {
        combination(prefix + letters[i], digits, idx + 1, res)
    }
}

Iterative Approach (BFS)

// bfs utility function
string[] combination(string digits, int n, string[] KEYS) { 
    string[] list
    Queue q
    q.push("")
    while (q is not empty) {
        string s = q.front()
        q.pop()
        // If complete word is generated push it in the list 
        if (s.length() == n)
            list.add(s)
        else
            for (letter in KEYS[int(digits[s.length()])]) 
                q.push(s + letter)
    }
    return list
}
// driver function
string[] letterCombinations(string digits) { 
    string KEYS[10] = { "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" }
    int n = digits.length()
    string[] res = combination(digits, n, KEYS)
    return res
}

Complexity Analysis

Time complexity: O(3^N×4^M)

where N is the number of digits in the input that maps to 3 letters and M is the number of digits in the input that maps to 4 letters, N+M is the total number digits in the input.

Space complexity: O(3^ N ×4^ M )

Critical Ideas To Think

Can we call the recursive solution as a backtracking solution?
Can you draw the recursion tree for some bigger input?
Why we only pushed those strings to result whose length is equal to the length of input digits?
What is the time complexity of iterative BFS? Is the time complexity for recursive and iterative approaches are same? If yes, then comment on their space complexities!
Comment down your iterative DFS approach for this problem!