What is recursion in programming?

What is Recursion??

Recursion is a way of solving problems via the smaller versions of the same problem. We solve the problem via the smaller sub-problems till we reach the trivial version of the problem i.e. base case.

“In order to understand recursion, one must first understand recursion.”

In other words, a recursive function is a function that calls itself until a “base condition” is true, and execution stops. The recursive function has two parts:

1. Base Case
2. Recursive Structure

Any recursive function will look like

function(arg1,arg2,....)
{
    if( Base Case Condition )
    {
        // Base Case
    }
    // Recursive Structure
    
}

Base Case: The smallest version of the problem for which we already know the solution or a terminating condition where a function can return the result immediately.

Recursive Structure: Finding the solution to a problem via the solution of its smaller sub-problems. Here function must call itself to break the current problem down to a simpler level.

Let us take an example of Countdown Problem to understand the base case and recursive structure.

Recursion Example 1: Countdown Problem

You need to print numbers from N to 1 in decreasing order.

Recursive Structure

In a recursive structure, we break the solution of the problem in terms of the solution of smaller versions of the same problem. So, here we can print N at the first step and call the same function to print the remaining N -1 numbers.

Printing numbers from N to 1 = print (N) + Printing numbers from N-1 to 1

Original Problem: Printing numbers from N to 1
Smaller subproblem: Printing numbers from N-1 to 1

=> countdown(N) = print(N) + countdown(N-1)

Now, The chain of the function call needs to stop somewhere. Just Think, what can be the base case for the above solution?

Base Case

The countdown needs to stop after printing 1. So we need to write a base condition to stop the program execution.

void countdown(int n)
{
    if( n < 1 ) // Base Case
    {
        return // stops the execution with return statement.
    }
}

Now, we just need to combine the recursive structure and base case to write the full recursive implementation of the above problem

Pseudo Code

void countdown(int n)
{
    if(n < 1 ) // Base Case
    {
        return
    }
    print(n)
    countdown(n-1) // Recursive 
}

Flow Chart of Program

Critical Ideas to Think!

• Think for a recursive solution to print numbers in increasing order (1 to N).

Recursion Example 2 : Factorial Problem

We need to find the nth factorial. The factorial of a number is the product of numbers from 1 to n (Inclusive). For Example, Factorial of 4 is 1*2*3*4 = 24

Recursive Structure

According to the definition of the factorial, we can describe a solution to a problem via the solution of its smaller sub-problem.

Finding nth factorial = n * finding (n-1)th factorial

Original Problem: finding nth factorial
Smaller sub-problem: finding (n-1)th factorial

fact(n) = n * fact(n-1)

Base Case

Now think about the base case, where the function will directly give you results without breaking it again into sub-problem.

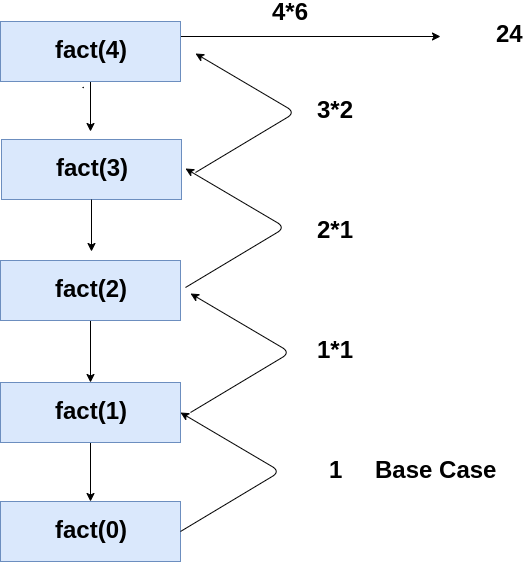
fact(5) 
= 5 * fact(4) 
= 5 * 4 * fact(3) 
= 5 * 4 * 3 * fact(2) 
= 5 * 4 * 3 * 2 * fact(1) 
= 5 * 4 * 3 * 2 * 1 * fact(0)

The factorial of a negative number is not defined, so fact(0) is the smallest version of the factorial problem where our solution will terminate.

Here n = 0 is the base case which will return 1. Since 0! = 1

Flow of Program

Pseudo Code

int fact(int n)
{
    if(n == 0) // Base Case
    {
        return 1
    }
    
    return n*fact(n-1) // Recursive Structure
}

Critical Ideas to Think

Take a problem “Reverse the String” and think about its recursive solution with the help of the above thought process.

Some famous Recursive Algorithms

Finding nth fibonacci

Recursive Structure
fibonacci(n)= fibonacci(n-1) + fibonacii(n-2)

Base Case
if (n <= 1) return n. 
Here we have 2 base cases: fib(0) = 0 and fib(1) = 1

Finding GCD of two numbers

Recursive Structure
gcd(a, b) = gcd(b, a mod b)
Here we are assuming that a > b

Base Case
gcd(a, 0) = a

Reverse an array

Recursive Structure
reverseArray(A, l, r)
- swap(A[l], A[r])
- reverseArray(A, l+1, r-1)

Base Case
If (l >= r) then return (Think!)

Binary Search

Recursive Structure
BinarySearch(A[], l, r, k)
- mid = l + (r-l)/2
- if (A[mid] > k), then call BinarySearch(A[], l, mid-1, k) 
- if (A[mid] < k), then call BinarySearch(A[], mid+1, r, k)

Base Case
If (l > r) then return -1. This is the case of unsuccessful search (Think!)

Merge Sort

Recursive Structure
mergeSort(A[], l,  r)
- mid = l+(r-l)/2
- Recursively sort first half : mergeSort(A, l, mid)
- Recursively sort second half: mergeSort(A, mid+1, r)
- Merge the two sorted halves: merge(A, l, mid, r)

Base Case
If (l == r) then return. This is the case of single element (Think!)

Quick Sort

Recursive Structure
quickSort(A[], l, r)
- pivot = partition(A, l, r)
- quickSort(A, l, pivot - 1)
- quickSort(A, pivot + 1, r)

Base Case
if (l >= r) then return. 
Here we have two base cases : (l > r) and (l == r)

In-Order Traversal of binary tree

Recursive Structure
Inorder(root)
- Traverse the left subtree: Inorder(root->left)
- Visit the root
- Traverse the right subtree: Inorder(root->right)

Base Case
if(root == NULL) then return

Print all permutation of a given string

Recursive Structure
permute(string A, l, r)
for(i = l to r)  
- swap(A[l], A[i])
- permute(A, l+1, r)
- swap(A[l], A[i])

Base Case
if(l == r) then print(A)(Think!)

Longest Common Subsequence

Recursive Structure
lcs(X, Y, m, n)  
- if(X[m-1] == Y[n-1]), return 1 + lcs(X, Y, m-1, n-1)
- else, return max (lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)) 
 
Base Case
if (m == 0 || n == 0) then return 0 

Idea of Recursion Call Stack

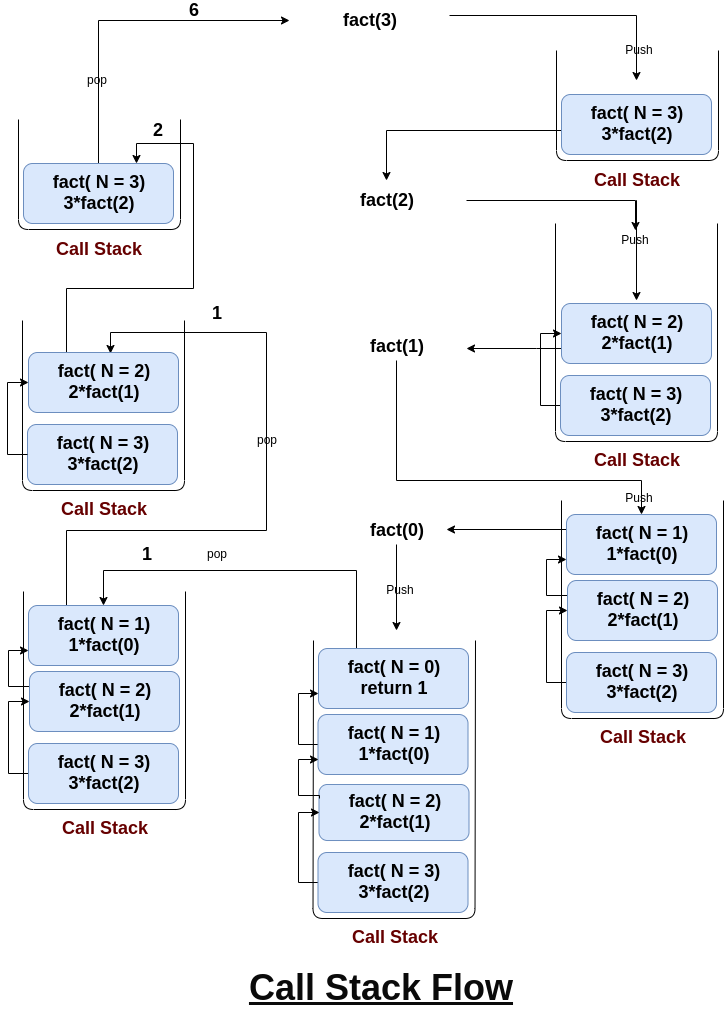
If we observe the above flow of execution of recursion, one pattern is visible: fact(0) get called last but returning the value first. Similarly, we are calling fact(n) first but returning the value last. (Think!)

Order of execution of function call

fact(n)-> fact(n-1)...-> fact(i)->...-> fact(1)-> fact(0)

Order in which functions are returning values

fact(0)-> fact(1)...-> fact(i)->...-> fact(n-1)-> fact(n)

The above idea looks similar to the Last In First Out(LIFO) order. Here are some key insights related to the execution of recursion:

• For the execution of the recursive functions, compiler use “Call Stack” which is based on the stack data structure.
• When a program calls a function, memory is allocated to it and it goes on the top of the call stack.
• The memory for a called function is allocated on top of memory allocated to calling function and different copy of local variables is created for each function call.
• When the base case is reached, the function returns its value to the function by whom it is called and memory is de-allocated and the process continues.

If you are not familiar with stack data structure, assume a stack of books. In this, you can add one book at a time. Then when have to take one out of it, you can take only that is on the top of the stack.

Let's see the call stack for factorial example

How to proceed with problem-solving using Recursion?

To solve any problem recursively, just try to follow these thought process, it will make it easier to decide the recursive structure and base cases :

1. How can we solve the same problem by using the solution of its smaller sub-problems?
2. Don't worry about the solution of smaller sub-problems because recursion will take care of it!
3. Write a recursive structure with function parameter and proper boundary conditions
4. Identify base cases i.e. the smallest version of the problem for which you already know the solution. What will happen if you choose the wrong base case or didn't write a base case? (Think!)
5. Understanding the nature of sub-problems are important in recursive solutions. For example :

• Divide and Conquer: Solving problems via more than one subproblems and sub-problems are independent.
• Dynamic programming: Solving problems via more than one subproblems and sub-problems are dependent

Application of Recursion

• Solving Array and Linked list problems
• Solving Tree Problems
• Solving Graph problems
• Problem Solving by Divide and Conquer Approach
• Problem Solving by Dynamic Programming
• Problem Solving by Exhaustive Search and Backtracking
• Well-known sorting algorithms like Quick sort, Merge sort
• Designing Approximation Algorithms

Why we need Recursion?

Here are some benefits of using recursion:

• A recursive solution is often cleaner than an iterative solution. We often find cases where a ~50 line for loop can be reduced to ~5–10 lines of recursion.
• In some cases, it's more natural to “think recursively”. Recursion is the clearest, simplest way to solve problems in data structures like trees where a recursive structure is simple to understand.
• There are some problems which are quite difficult or impossible to solve with Iteration.
• Recursion naturally breaks problems into smaller, independent subproblems, which substantially makes it easier to parallelize.

Critical Concepts to explore in Recursion

• Analysis of recursion by Recursion Tree Method
• Analysis of recursion by Master Theorem
• Advantages and disadvantages of recursive programming
• Different Types of recursion and properties
• Iteration vs Recursion comparison
• Why Stack Overflow error occurs in recursion?
• How to convert recursive code into iterative code and vice versa?

Suggested Problems to solve in Recursion

• Find an element in Bitonic array
• Search for a Range in a sorted array
• Missing Number
• Search a 2-D Matrix
• Median in row wise sorted matrix
• Find minimum element in sorted and rotated array
• Recursive Insertion Sort
• Median of two sorted array of same size
• Inversion count in an array
• Longest Common Prefix

Happy coding! Enjoy Algorithms.