Topological Sorting

In this blog, we will discuss Topological sort in a Directed Acyclic Graph i.e. DAG. We will discuss the following things:

• What is the Topological Sort?
• How can we find Topological Ordering?
• Illustration using a Directed Acyclic Graph
• Pseudo Code
• Applications of Topological Sorting

Prerequisites

• Introduction to Graph in Programming
• Graph Traversal: Depth First Search
• Graph Traversal: Breadth-First Search

What is Topological Sort

In the Directed Acyclic Graph, Topological sort is a way of the linear ordering of vertices v1, v2, …. vN in such a way that for every directed edge x → y, x will come before y in the ordering.

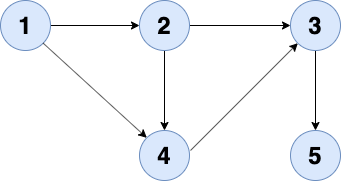
For example-The topological sort for the below graph is 1, 2, 4, 3, 5

Important Points to remember

• There can be multiple topological ordering for a Directed Acyclic Graph.
• In order to have a topological sorting, the graph must not contain any cycles and it must be directed i.e. the graph must be a DAG. (Think!)

How to find Topological Sort

Topological order can be one of the subsets of all the permutations of all the vertices following the condition that for every directed edge x → y, x will come before y in the ordering.

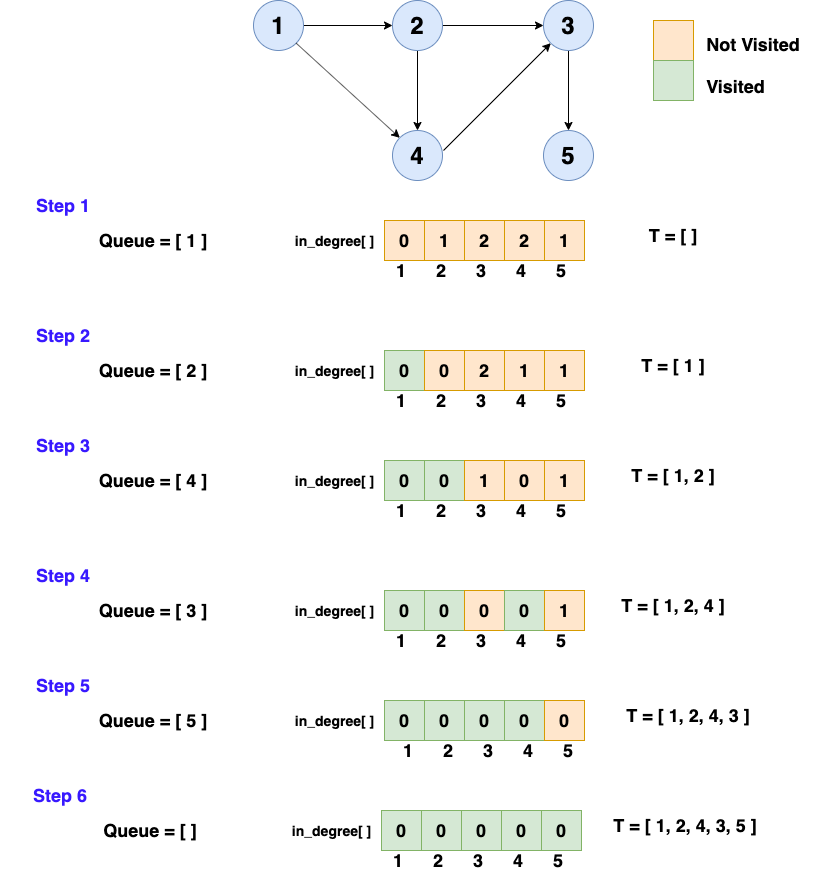
For that, we will maintain an array T[ ], which will store the ordering of the vertices in topological order. We will store the number of edges that are coming into a vertex in an array in_degree[N], where the i-th element will store the number of edges coming into the vertex i. We will also store whether a certain vertex has been visited or not in visited[N]. We will follow the belo steps:

• First, take out the vertex whose in_degree is 0. That means there is no edge that is coming into that vertex.
• We will append the vertices in the Queue and mark these vertices as visited.
• Now we will traverse through the queue and in each step we will dequeue() the front element in the Queue and push it into the T.
• Now, we will put out all the edges that are originated from the front vertex which means we will decrease the in_degree of the vertices which has an edge with the front vertex.
• Similarly, for those vertices whose in_degree is 0, we will push it in Queue and also mark that vertex as visited. (Hope you must be thinking its BFS but with in_degree)

Illustration

Pseudo Code

topological_ordering(int N, bool adj[N][N]) 
{
    int T[]
    bool visited[N]
    int in_degree[N]
    
    for ( i = 0 to N-1 )
        in_degree[i] = visited[i] = false
    
    for ( i = 0 to N-1 )
        for ( j = 0 to N-1 )
            if (adj[i][j] == true)
                in_degree[j] += 1
                
    Q = Queue()
    
    for ( i = 0 to N-1 )
    {
        if ( in_degree[i] == 0 ) {
            Q.enqueue(i);
            visited[i] = true
        }
    }
    
    while( Q.size() != 0 )
    {
        curr = Q.front()
        Q.dequeue();
        T.append(curr);
        for( j = 0 to N-1 )
        {
            if ( adj[curr][j] == true and visited[j] == false)
            {
                in_degree[j] -= 1
                if (in_degree[j] == 0)
                {
                    Q.enqueue(j)
                    visited[j] = true
                }
            }
        }
    }
    
    return T
}

Applications

• Scheduling jobs from given dependencies among Jobs. For example, if some job requires the dependency of some other job, then we can use topological sorting.
• Instruction Scheduling
• Determining the order of compilation tasks to perform in makefiles, data serializations and resolving symbol dependencies in linkers.
• Use in maven dependency resolutions.

Critical Ideas to Think

• The above approach uses the BFS traversal technique. Can it be solved using the DFS traversal technique?
• What can be the modifications that can be done if we have been given the Adjacency matrix?

Graph questions

• Is Graph Bipartite?
• Number of Islands
• Word Ladder Problem
• Smallest Multiple with 0 and 1
• Course Schedule
• Knight on Chessboard

Happy Learning, Enjoy Algorithms!

Team AfterAcademy!