Calculate power function

Understanding the Problem

Given two integers x and n, write a function to compute x^n (x to the power n). You may consider that x and n are small and overflow doesn’t happen.

Example — 

power(3,4) = 81
power(2,-3) = 0.125

Solutions

1. Naive Iterative approach
2. Divide and Conquer approach
3. Optimized divide and conquer approach

1. Naive Iterative approach

The most basic way to calculate the nth power of a number is to multiply that number exactly n-times.

What if n is negative, like pow(2,-3) = 0.125

In this case, we could just find the inverse of its positive power i.e. pow(2,-3) = 1/(2^3).

Solution steps

1. Declare and initialize a variable to store power say power = 1.
2. Run a loop from 1 to exponent, increment loop counter by 1 in each iteration.
3. For each iteration inside loop multiply power with the number.
4. For negative exponent, return 1/power Otherwise, return power

Pseudo Code

float power(int base, int expo){
    bool isNegative = False
    if(expo < 0){
        isNegative = True
    }
    float power = 1
    for(int i = 1 to abs(expo)){
        power = power * base
    }
    if(isNegative) {
       return (1/power)
    }
    return power
}

Complexity Analysis

Time Complexity — O(n) or O(exponent)

Space Complexity — O(1)

Critical Ideas to Think

• Will the algorithm work if the input base is negative?
• Will the algorithm work if the input exponent is negative?
• Are you able to think of a better approach to solve it?

2. Divide and Conquer approach

The Divide & Conquer approach squares the number each time, rather than multiplying it with the number itself.

Now if we try to visualize this process recursively, then it would be like this →

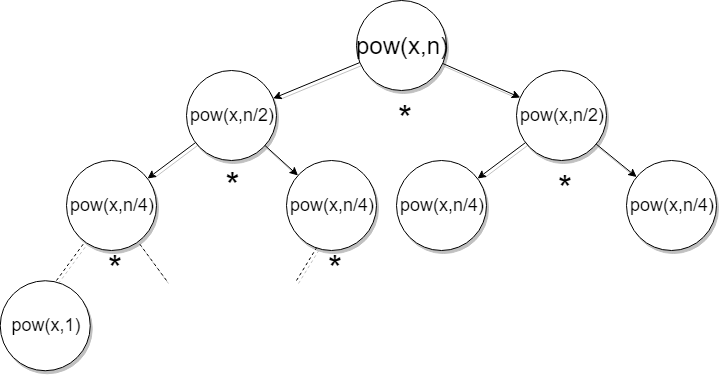
Example — If we want to compute 3⁸ we actually compute it like

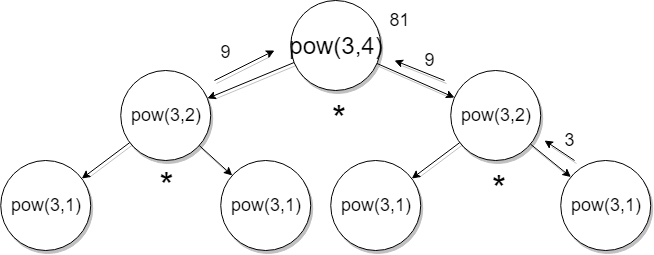
So the recursive definition would be →

if exponent is even :
power(base, expo) = power(base, expo/2) * power(base, expo/2)
if exponent is odd :
power(base, expo) = base * power(base, expo/2)*power(base, expo/2)

Solution steps

1. Check if the exponent is 0 then return 1 otherwise
2. On the basis of even or odd, call the power function recursively as defined above.

Pseudo Code

float power(int base,  int expo) { 
    if (expo is 0) 
        return 1
    if (expo % 2 == 0)
       return power(base, expo / 2) * power(base, expo / 2)
    else {
       if(expo > 0)
           return (power(base, expo / 2) * power(base, expo / 2))* base
       else
           return (power(base, expo / 2) * power(base, expo / 2))/ base
    }
}

Complexity Analysis

Time Complexity — O(n) or O(exponent)(Why?)

Space Complexity — O(log(n)) (Think!)

Critical Ideas to Think

• Can you point out repeating calculations?
• Will this algorithm work for a negative exponent value?

3. Optimized divide and conquer approach

If you will look over the previous divide and conquer approach recursive diagram, you will find out that at each step we are recalculating the power of the base at each level i.e. same power is counted twice.

So, instead of calling the power function twice recursively, we could just square the power function once. In this way, we could optimize the time complexity.

Pseudo Code

float power(int base,  int expo) { 
    if (expo is 0) 
        return 1
    temp = power(base, expo/2)
    if (expo % 2 == 0)
       return temp * temp
    else{
       if(expo > 0)
           return temp * temp * base
       else 
           return temp * temp / base
    }
}

Complexity Analysis

Time Complexity: O(log n) or O(log expo)

Space Complexity: O(log n) or O(log expo) due to recursive stack space

Critical Ideas to Think

• Can you think of a better approach than this?
• Dry run this algorithm on a few examples.

Comparison of Different Solutions

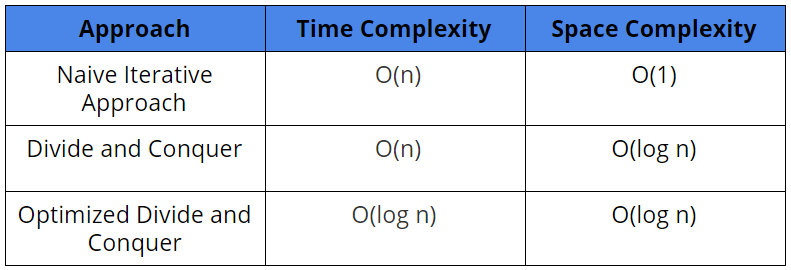
Suggested Problems to Solve

• Calculate the square root of a number
• Calculate the value of nCr

That's it for this blog. Hope you learned something new today.

Happy Coding, Enjoy Algorithms!