When to Convert a 2-D DP Array To 1-D DP Array And How?

In which situation a 2 dimensional DP can be dropped to 1 dimension? Is there any principle or regular pattern?

Yes , the magic is the observation from the induction rule/recurrence relation!

Consider " Partition Equal Subset problem as an example", the induction rule:

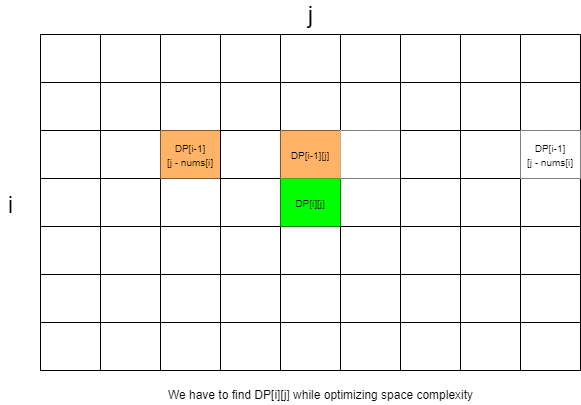
1. If not picking nums[i - 1] , then dp[i][j] = dp[i-1][j]
2. If picking nums[i - 1] , then dp[i][j] = dp[i - 1][j - nums[i - 1]]

You can see that if you point them out in the matrix, it will look something like this:

1. Optimize to O(2*n) : You can see that dp[i][j] only depends on the previous row, so you can optimize the space by only using 2 rows instead of the matrix. Let's say array1 and array2 . Every time you finish updating array2 , array1 has no value, you can copy array2 to array1 as the previous row of the next new row.
2. Optimize to O(n) : you can also see that, the column indices of dp[i - 1][j - nums[i] and dp[i - 1][j] are <= j . The conclusion you can get is: the elements of the previous row whose column index is > j (i.e. dp[i - 1][j + 1 : n - 1] ) will not affect the update of dp[i][j] since we will not touch them:

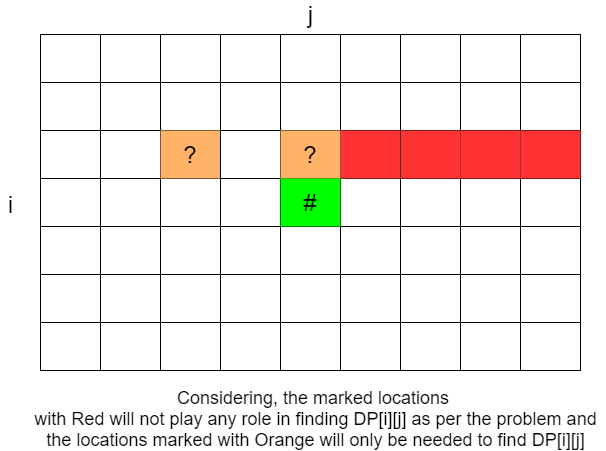
Thus if you merge array1 and array2 to a single array named array , and if you update array backward, all dependencies are not touched!

However, if you update forwards, dp[j - nums[i - 1]] is updated already, you cannot use it:

You may refer to the Dynamic Programming approach of Partition Equal Subset Sum Problem blog written here on Afteracademy.

Conclusion:
So the rule is that observe the positions of the current element and its dependencies in the matrix. Mostly if current elements depend on the elements in the previous row(most frequent case)/columns, you can optimize the space.

If you have any more approaches or you find an error/bug in the above solutions, please comment down below.

Happy Coding!

Enjoy Algorithms!