Partition Equal Subset Sum

Difficulty: Medium

Asked in: Amazon, Adobe

Given a non-empty array of positive integers arr[]. Write a program to find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.

Example 1

Input: arr[] = [1, 6, 11, 6] 
Output: true  
Explanation: The array can be partitioned as [6, 6] and [1, 11].

Example 2

Input: arr[] = [2, 6, 7]
Output: false
Explanation: The array cannot be partitioned into equal sum sets

Solutions

We will be discussing three different approaches to solve the problem

1. Brute Force: Check if any one of the combinations of all the possible combinations of the input array sums up to sum/2 then return true or false accordingly.
2. Dynamic Programming: Add a dp array to the brute force to remember the previous results at each step so that a redundant calculation can be avoided.
3. Using Bitset: Transform condition checks of dp to bitwise shift operations.

1. Brute Force

The idea is to calculate the sum of all elements in the set. A simple observation would be if the sum is odd, we cannot divide the array into two sets. Now, If the sum is even, we check if the subset with sum/2 exists or not.

We can consider each item in the given array one by one and for each item, there are two possibilities →

1. We include the current item in the subset and recur for remaining items with the remaining sum.
2. We exclude the current item from the subset and recur for remaining items.

Finally, we return true if we get subset by including or excluding the current item else we return false. The base case of the recursion would be when no items are left or sum becomes negative.

We can return true when sum becomes 0 i.e. subset is found.

Solution Steps

• Call a recursive canPartUtil function which checks if there exists a subset whose sum is equal to target, i.e sum/2
• The base case for the recursive function will be → if the target becomes 0, then the subset exists.
• At each index i, make two choices to look for the result,

1. Whether including the element at the ith index in the subset results in our desired answer.
2. Whether excluding the element at the ith index in the subset results in our desired answer.

Pseudo Code

public boolean canPartition(int[] nums, int n) {
    if(n <= 1)
        return false
    int sum = 0
    for(int i = 0 to i < n)
        sum = sum + nums[i]
    if((sum % 2) != 0)
        return false
    int target = sum/2
    //now the problem becomes can we use any combination of numbers in the nums[] to achieve the target
    return canPartUtil(0,target,nums)
}
boolean canPartUtil(int i,int res,int[] nums){
    if(i == nums.length or res < 0)
        return false
    if(res == 0)
        return true
    return canPartUtil(i+1,res -  nums[i],nums) or  canPartUtil(i+1,res,nums)
    //At each step all the way to the end of the array, you have only two choices: pick current number/ ignore it 
}

Complexity Analysis

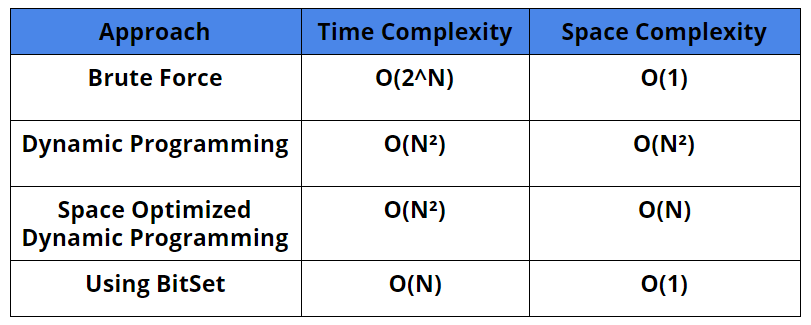
Time Complexity: O(2^n)

Space Complexity: O(1), if not considering recursion stack space.

Critical Ideas To Think

• Did we find out all the combinations of the nums array?
• Can you draw the recursion tree for a small example?
• Can you find out the recurrence relation?

2. Dynamic Programming

We know that if we can partition it into equal subsets that each set’s sum will have to be sum/2. If the sum is an odd number we cannot possibly have two equal sets.

This changes the problem into finding if a subset of the input array has a sum of sum/2.

We know that if we find a subset that equals sum/2, the rest of the numbers must equal sum/2 so we’re good since they will both be equal to sum/2. We can solve this using dynamic programming similar to the knapsack problem.

You may say that this is a 0/1 knapsack problem, for each number, we can pick it or not.

Let us assume dp[i][j] means whether the specific sum j can be gotten from the first i numbers. If we can pick such a series of numbers from 0-i whose sum is j, dp[i][j] is true, otherwise it is false.

Base Case: dp[0][0] is true since with 0 elements a subset-sum of 0 is possible (both empty sets).

dp[i][j] is true if dp[i-1][j] is true (meaning that we skipped this element, and took the sum of the previous result) or dp[i-1][j- element’s value] assuming this isn’t out of range(meaning that we added this value to our subset-sum so we look at the sum — the current element’s value).

If dp[n][sum/2] is true that means we were able to find a sum of sum/2 out of n elements which is what we want to check.

Solutions Steps

• For each number at index i (0 <= i < num.length) and sum s (0 <= s <= S/2), we have two options:

1. Exclude the number. In this case, we will see if we can get j from the subset excluding this number: dp[i-1][j]
2. Include the number if its value is not more than ‘j’. In this case, we will see if we can find a subset to get the remaining sum: dp[i-1][j-num[i]]

• If either of the two above scenarios is true, we can find a subset of numbers with a sum equal to ‘s’.

Pseudo Code

bool canPartition(int[] nums, int n) {
    int sum = 0
    for(int num in nums){
        sum = sum + num
    }
    if( sum%2 != 0)
        return false
    sum = sum/2
    bool [n+1][sum+1] dp
    dp[0][0] = true
    for(int i=1 to i <= n){
        for(int j=0 to j <= sum){
            if(j-nums[i-1] >= 0){
                dp[i][j]=dp[i-1][j-nums[i-1]]
            }
            dp[i][j] = dp[i][j] or dp[i-1][j]
        }
    }
    return dp[n][sum]
}

Complexity Analysis

Time Complexity: O(n²)

Space Complexity: O(n²)

Since we only use the current i and previous i, the rest of the indexes are a waste of space and we can reduce it to O(sum) space.
You can have a previous array and current array storage of length O(sum) or just traverse the i elements in the opposite order so they aren’t overwritten, both work with the same time complexity.

dp[i-1][j] won’t need to be checked since dp[j] will already be set to true if the previous one was true.

Pseudo Code

bool canPartition(int[] nums, int n) {
    int sum = 0
    for(int num in nums){
        sum= sum + num
    }
    if(sum%2!=0)
        return false
    sum = sum / 2
    bool [sum+1] dp
    dp[0] = true
    for(int i=1 to i <= n){
        for(int j = sum; j>=0; j=j-1){
            if(j-nums[i-1] >= 0){
                dp[j] = dp[j - nums[i-1]] or dp[j]
            }
        }
    }
    return dp[sum]
}

Complexity Analysis

Time Complexity: O(n²)

Space Complexity: O(n)

Critical Ideas To Think

• In which situation 2 dimensional DP can be dropped to 1 dimension? Is there any principle or regular pattern?
• Why the inner-loop should be from sum to num but not num to sum? Answer: If you see the solution that uses a 2D array, we see that our current row is updated with the values from the previous row. When we use a boolean array only. if we traverse from left to right, the leftmost value gets updated and its previous value gets replaced. For the elements on the right, we need the old values of the leftmost elements, not the updated ones. When we traverse from right to left, we are using the old values to update our boolean array.

3. Using BitSet

In the previous approach, dp[j] represents whether a specific sum value j can be gotten from (a subset of) nums or not. The basic idea was -> if dp[j] is achievable, then dp[i+num] is achievable if we pick the number num, and dp[i] is also achievable if we don't.

Thinking of the solution with bitset. One can replace the dp table with a bitset, a bit bits[j] has the same meaning as dp[j].

With the advantage of bitset, the inner loop of traversing dp, condition check of dp[j] are all transformed into bitwise shift operation, which is much more efficient.

Example, nums=[2, 3, 5], initial bits is 1, traversing through nums

• When num=2, bits=101, which represents nums can sum to 0 and 2
• When num=3, bits=101101, which represents nums can sum to 0, 2, 3, 5
• When num=5, bits=10110101101, which represents nums can sum to 0, 2, 3, 5, 7, 8, 10

Finally, we just need to check if bits[5] is 0 or 1.

You can say that, for each new value, we are just shifting bits to the left by that many places and then performing the OR operation with its previous state. The 1’s left in the bitset will represent that there exists a sum equal to the index that will be equal to the sum of one of the subsets of the nums array.

Solution Steps

• Create a bitset of size MAX_NUM*MAX_ARRAY_SIZE / 2 .
• Store the sum of all elements in a sum variable
• For each i , shift bitset by nums[i] and then perform bitwise OR with its previous state.
• Check if sum is even and bits[sum/2] is 1 , then return True, otherwise, return False

Pseudo Code

bool canPartition(int[] nums, int n) {
    int MAX_NUM = 100
    int MAX_ARRAY_SIZE = 200
    bitset<MAX_NUM * MAX_ARRAY_SIZE / 2 + 1> bits(1)
    int sum = 0
    for (int i=0 to i<n) {
        sum = sum + nums[i]
        bits |= bits << nums[i];
    }
    if ( !(sum % 2) and bits[sum / 2] )
        return true
    return false
}

Complexity Analysis

Time Complexity: O(n)

Space Complexity: O(1), size of the bitset will be 1256 bytes

Critical Ideas To Think

• What is the time complexity of bitset operations?
• Why we are shifting the bitset to the left for each new value?
• Take an example or a sample test case by yourself and dry run all the different approaches discussed above.

Comparison of Solutions

Suggested Problems to Solve

• Partition to K Equal Sum Subsets
• Maximum average sum partition of an array
• Count number of ways to partition a set into k subsets
• Minimum cost to partition the given binary string
• Number of ways to partition a string into two balanced subsequences

If you have any more approaches or you find an error/bug in the above solutions, please comment down below.

Happy Coding!

Enjoy Algorithms!