What is the difference between iteration and recursion?

Recursion and iteration are just two different code structures with the same end result: Execution of a set of sequential instructions repeatedly.

The emphasis of Iteration: The repeated execution of some groups of code statements in a program until a task is done.

The emphasis of recursion: Here we solve the problem via the smaller sub-problems till we reach the trivial version of the problem i.e. base case.

Comparison: Iteration vs Recursion

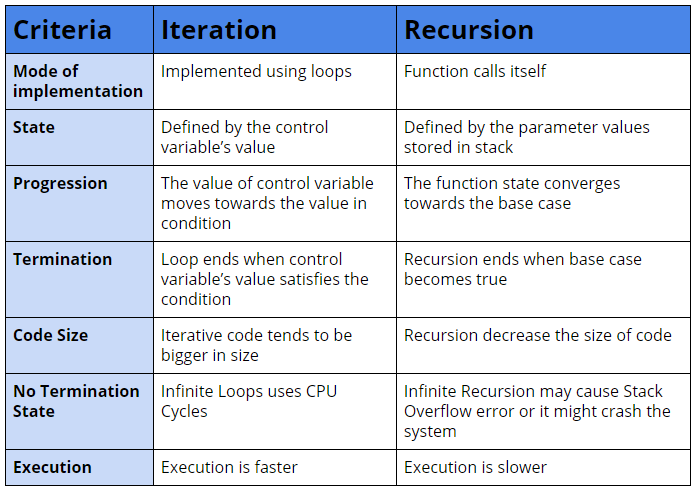
Which is better: Iteration or Recursion?

1. Sometime finding the time complexity of recursive code is more difficult than that of Iterative code. (Think!)
2. Recursion has a large amount of overhead as compared to Iteration. It is usually much slower because all function calls must be stored in a stack to allow the return back to the caller functions. Iteration does not involve any such overhead.
3. Infinite recursion can lead to CPU crash because infinite recursive calls may occur due to some mistake in base condition, which on never becoming false, keeps calling the function, which may lead to system CPU crash.
4. Infinite iteration due to mistake in iterator assignment or increment, or in the terminating condition, will lead to infinite loops, which may or may not lead to system errors, but will surely stop program execution any further.
5. Every recursion can be modeled as a kind of loop, that's what the CPU will ultimately do. And the recursion itself, more directly, means putting the function calls and scopes in a stack. But changing your recursive algorithm to a looping one might need a lot of work and make your code less maintainable.

If recursion is usually slower then what is the technical reason for using it over iteration?

• Because some algorithms are hard to solve it iteratively. Try to solve the depth-first search both recursively and iteratively. You will get the idea that it is plain hard to solve DFS with iteration. Try to write Merge sort iteratively. It will take you quite some time.
• It's more intuitive in many cases when it mimics our approach to the problem. For example, Data structures like trees are easier to explore using recursion (or would need stacks in any case)

Comparative Examples

We will now see the code of following questions implemented as both recursion and iteration to help you better see the difference

Example 1: Finding nth Fibonacci number

• Recursive Code

int fib(int n)
{
    if(n <= 1)
    {
        return n
    }
    return fib(n-1) + fib(n-2)
}

• Iterative Code

int fib(int n)
{
    if( n <= 1 )
        return n
    a = 0, b = 1
    for( i = 2 to n )
    {
        c = a + b
        a = b
        b = c
    }
    return c
}

Complexity Analysis

• Time complexity of recursive code = O(2^n)
• Time Complexity of iterative code = O(n)
• Space Complexity of recursive code = O(n) (for recursion call stack)
• Space Complexity of iterative code = O(1)

Critical ideas to think!

• Here recursive algorithm is a little difficult to analyse and inefficient in comparison with the iterative algorithms.

Example 2: In-order traversal of a binary tree

• Recursive Code

void inorderRecursive(Node root)
{
    if( root == NULL )
        return
    inorderRecursive(node.left)
    print(root.data)
    inorderRecursive(node.right)
}

• Iterative Code

void inorderIterative(Node root) 
{ 
    Node current, pre 
  
    if (root == NULL) 
        return
  
    current = root
    while (current != NULL) { 
  
        if (current.left == NULL) { 
            print(current.data)
            current = current.right
        } 
        else 
        { 
            pre = current.left
            while (pre.right != NULL && pre.right != current) 
                pre = pre.right
            if (pre.right == NULL) 
            { 
                pre.right = current
                current = current.left 
            } 
            else
            { 
                pre.right = NULL 
                print(current.data)
                current = current.right
            }
        }
    }
}

Critical Ideas to think

• Worst-case time and space complexities of both the approaches are nearly same but the recursive approach looks intuitive, clean and easy to understand.
• The iterative code is longer with complex flow and implementation. The complex part in the iteration is the stack maintenance which is done by the compiler in recursion.

Example 3: Insertion Sort

• Recursive Code

void insertionSortRecursive(int A[], int n) 
{ 
    if (n <= 1) 
    insertionSortRecursive(A, n-1)
    int last = A[n-1]
    int j = n-2
    while (j >= 0 && A[j] > last) 
    { 
        A[j+1] = A[j]
        j-- 
    } 
    A[j+1] = last
} 

• Iterative Code

void insertionSort(int A[], int n)  
{  
    int i, key, j
    for (i = 1 to n-1) 
    {  
        key = A[i]
        j = i - 1
        while (j >= 0 && A[j] > key) 
        {  
            A[j + 1] = A[j]
            j = j - 1
        }  
        A[j + 1] = key
}  

Complexity Analysis

• Time complexity of recursive code = O(n)
• Time Complexity of iterative code = O(n)
• Space Complexity of recursive code = O(n) (for recursion call stack)
• Space Complexity of iterative code = O(1)

Critical ideas to think!

• Here the recursive algorithm is difficult to analyse and less intuitive to think. It includes the overhead of function calls and recursion call stack.
• The Iterative approach looks intuitive, clean and easy to understand.

More examples of Iteration and Recursion

• Traversal of trees: Recursive
• Dynamic Programming: Both recursive and Iterative
• Traversal of linear Data Structure: Iterative
• Depth-First Search: Recursive
• Breadth-First Search: Iterative
• Backtracking Algorithms: Recursive
• Divide-and-Conquer problems: Recursive in nature.
• Hash Table: Iterative
• Greedy: Both recursive and Iterative
• BST: Both Iterative and Recursive

Happy Coding! Enjoy Algorithms!

AfterAcademy Data Structure And Algorithms Online Course - Admissions Open