The Concept of Hashing in Programming

Hashing is one of those topics that the interviewer will ask you in every interview because with the help of hashing, you can perform the insertion, deletion, and searching operation in O(1) time. Yes, you heard it right. So, in this blog, we will learn about how the idea of Hashing works in Programming. By the end of the blog, you will have a basic idea about the following topics:

• Direct Address Table
• Hash Table
• Hash Function and its properties
• The idea of collision in the Hash Table
• Collision resolution techniques: Chaining and Open Addressing
• Critical Ideas to think in Hashing
• Suggested problems to solve in Hashing

So, let's get started with some basics of Hashing.

Basics of Hashing

Hashing is a way to store data into some data structure (generally Hash Table is used) in such a way that the basic operations on that data i.e. the insertion, deletion, and searching can be performed in O(1) time. Here data is stored in the form of key-value pairs i.e. for each data you will assign some key and based on that key the insertion, deletion, and searching of your data will be performed.

So, let's dive deeper into the concept of hashing by learning about the basic version of the hash table i.e. Direct Address Table.

Direct Address Table

Direct Address Table is the basic version of the Hash Table where we use a simple array-like structure to store the data related to each key. For example, if your keys are in the range from 0 to 99, then you will create a table of size 100 and you will store all the data related to the keys in that table. So, to store data related to key with value 10, you can store it at index number 10. Similarly, for storing data related to key 55, you can store it at index number 55.

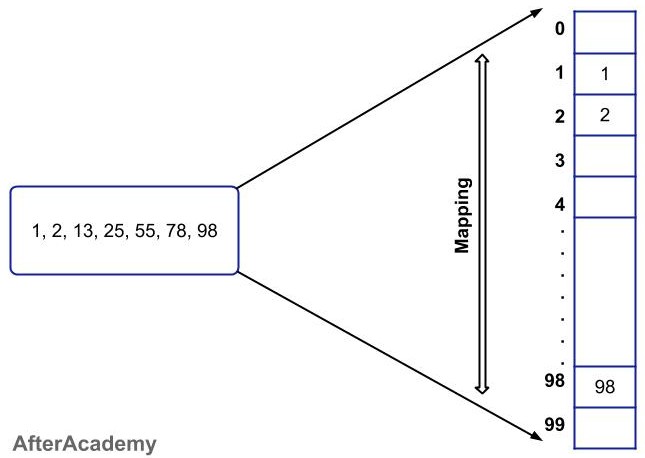
By following the above approach, the insertion, deletion, and searching will be in O(1). Let's see how?

• Insertion: When you have some key-value pairs and you want to store it in the Direct Address Table, then all you need to do is create a table of size m where "m" is the number of all possible keys. Then you can store the data related to each key in the table just by accessing that index. For example, if the key is 5 and the range of keys can be in between 0-9, then the data related to key "5" will be stored at index 5 (arr[key] = data) and this can be done in O(1) time.
• Deletion: For the deletion operation, you can access the element to be deleted in O(1). For example, if you want to delete the data related to key with value "5", then since you are using Direct Address Table, arr[5] will be the location where the data is stored. So, just delete it in O(1) time.
• Searching: Searching operation can also be performed in O(1) time because the key to be searched can be directly found by accessing that index. For example, if you want to search the data related to the key with value "5", then we know that it will be stored at arr[5], so we can directly get the data in O(1) time.

Problem with Direct Address Table

In the Direct Address Table method if there are "n" possibilities of the keys, then we will create a memory for all those "n" possibilities. But in reality, we have a very low number of keys that are needed to be stored in the created table.

For example, if the keys can lie in between 0 - 9999, then we will create a Direct Address Table for all the 10,000 keys. Now, we have only 10 keys to store in that table. So, the rest of the 9990 places will be left vacant in our table. So, this is the major drawback of using the Direct Address Table.

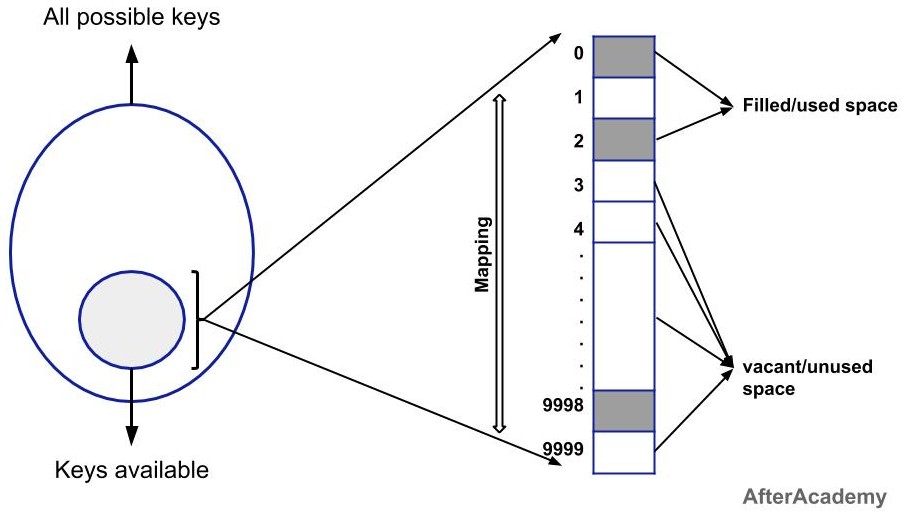
We can reduce the unnecessary space with the help of the Hash Table.(Think!)

Hash Table

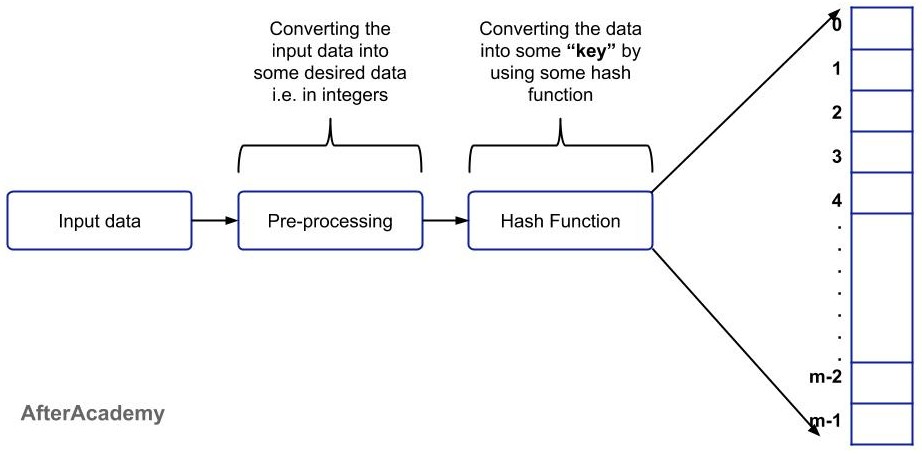
In a Hash Table, to store data we use Hash function that takes the data as input and based on that data it generates some key and we store the data based on that key.

Our data can be of any form i.e. it can be in integer or string or some other data type. But our main aim should be to convert that data into an integer by doing some preprocessing and then apply some hash function to it and map the result in the hash table.

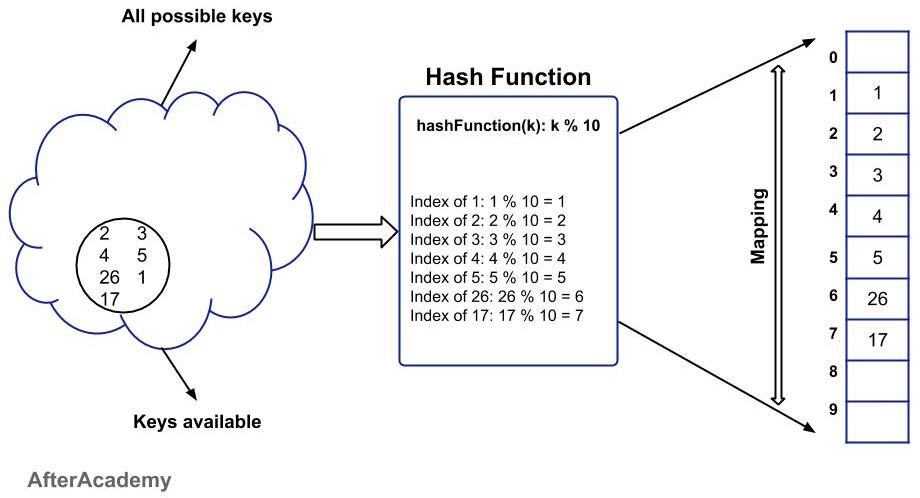
For example: If the data that is to be stored is 2, 3, 4, 5, 26, 17 and our hash function is:

hashFunction(k): k % 10

Here, in the above example, we are finding the remainder of any data and that remainder is our key and based on that we are storing the value in the hash table. So, the maximum possible cases of keys can be 0-9 (because we are using the modulus of 10 and in this case, the remainder can never exceed 9). Following is the representation of the above example:

Let's take another example where we want to store some strings in the hash table. Here, we will pre-process our data(by taking the sum of alphabets i.e. if the string is "ab" then the sum will be "1+2 = 3") and then based on this we will use the hash function to generate our key.

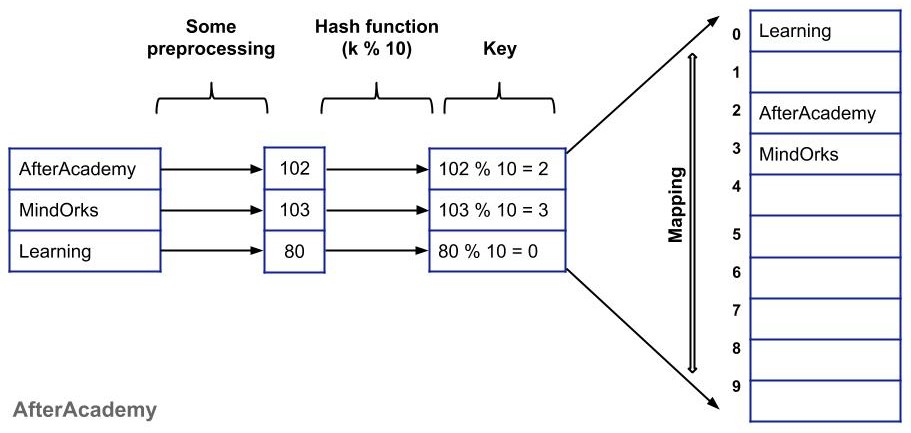
Let's see how we can perform Insertion, Deletion, and Searching in O(1) using Hash Table:

• Insertion: Here, we are using a hash function, so the hash function will generate the key in O(1) time because we are using mathematical calculations in hash function and we can directly go to that address without any traversal. So, the overall time complexity of the insertion of data in the hash table is O(1).
• Deletion: In order to delete an element from the hash table, we can use the hash function to find the position of the element in the hash table and go directly to that place and directly delete that item. So, the overall deletion operation can be performed in O(1).
• Searching: The hash function can be used to search the index of particular data. All you need to do is just pass the data value in the hash function and the hash function will return the index where the data is being stored. So, the searching operation can be performed in O(1) time.

Some of the commonly used Hash Functions are:

hashFunction(k): | k * m |, if 0 <= k <= 1
hashFunction(k): k mod m

You can design your own Hash Function according to the need of the problem. (Think!)

Problem with the Hash Table

So, we have seen how we can insert, delete, and search data in a Hash Table using O(1) complexity. But there is some problem with the hash table also.

For example, let's take the same hash function as used above i.e.

hashFunction(k): k % 10

The data that is to be stored is 11, 22, 32, 33, 105, 125, and 129. Now, if you apply the above hash function on these values, then the generated keys will be 1, 2, 2, 3, 5, 5, and 9. So, some keys are repeating like 2 and 5. Firstly, 22 will be stored on index number 2 and when "32" will come, then it will also have the same key i.e. "2" and it will find that index number 2 is already taken by "22". So, there is a collision between 22 and 32. Here, in our example, we are having two collisions but in real-life problems, we can have a number of collisions in our hash table and this should be avoided.

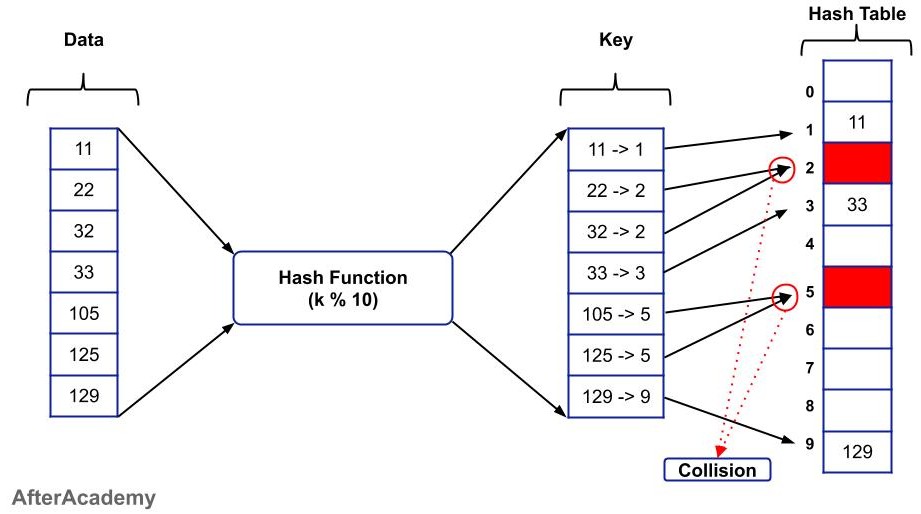
Collisions can be removed by having a uniformly distributed keys and this can be achieved by using a good hash function. The common hash function used for this purpose is:

hashFunction(k): k % p, here p is some prime number

But it is not a guarantee that collision will never happen in your code.(Think!) So, we must know how to remove collision if it occurs in some hash table. So, let's understand how to resolve the situation when there is a case of collision.

Collision resolution techniques

Whenever a collision occurs in a hash table, then that collision can be resolved using two techniques:

1. Chaining
2. Open Addressing

Chaining

Chaining is a collision resolution technique where we make use of the linked list or list data structure to store the keys that are having the same value.

For example, if the data is 2, 22, 33, 40, and 50, and the hash function is:

hashFunction(k): k % 10

then from the above hash function, we can conclude that:

hashFunction(2) = hashFunction(22) = 2
hashFunction(40) = hashFunction(50) = 0

Both these values can't be stored in the same place in the hash table. So, we make use of the linked list and store the data by performing the following steps:

• We make a hash table of "m" size, where "m" is the total number of possible combinations of keys that can be generated from the hash function.
• Every entry in the hash table will correspond to a linked list i.e. the hash table will contain the head address of the linked list that is associated with that position.
• If some key comes into the hash table and the head is null, then we will directly insert that value in the head node.
• If the data is already there i.e. in the case of collision, we can create a node and insert the node next to the head node.

For example: If the data is 3, 23, 24, 26, 36, 46, 78, and 99, and the hash function is:

hashFunction(k): k % 10

then the storage of the data in the hash table can be represented as:

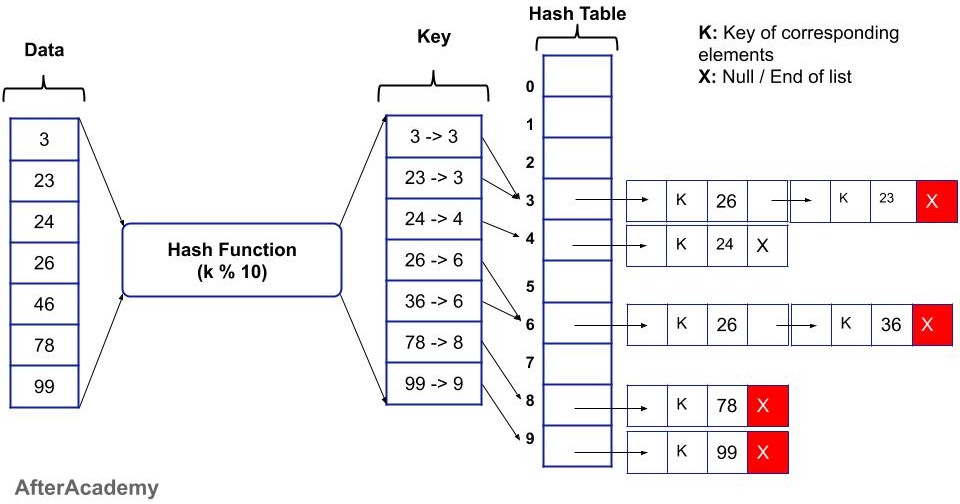
Now, let's see the time complexity of our basic three operations i.e. insertion, deletion, and searching.

• Insertion: For inserting data into the hash table, we will generate a key "k" with the help of a hash function. In the hash table, we will go to the index "k" and find if some element is already there in the hash table or not. If there is no element present in the hash table then we can simply add the data to the head node and if there is some data at the index "k", then we can create a node and store the created node either before the head node or we can traverse to the end of the linked list and insert the node at the end of the list. So, in the case of traversing i.e. in the worst case, the time complexity of insertion of data will O(n). But if the keys are uniformly distributed by the hash function, then the time complexity will be of O(1) time average.
• Deletion: The deletion operation in the chained hash table is similar to that of deletion of a node from the linked list. All you need to do is enter the data that is to be deleted in the hash function and from the hash function, you can get the key and with the help of key, you can directly traverse to the data node that you want to delete and then you can delete it just like deleting some node from the linked list.
• Searching: For the searching operation, enter the data that you want to search in the hash function and from the hash function, you will get the key and with the help of the key, you can go to the location where the data is stored. There either you will find the element at the head node or you have to traverse the whole list for finding the desired node. So, the linked list traversal may take O(n) time in the worst case. But if the keys are uniformly distributed by the hash function, then the time complexity will be of O(1).

In this way, we can remove the collision in the hash table with the help of chaining. There is one another method called the Open Addressing to remove chaining. Let's see how collision can be removed with Open Addressing.

Open Addressing

In the chaining technique, we have to use some variable that is pointing to a list associated with a particular index. Also, there is not a full utilization of space of the hash table. For example, if we have 2 and 22, and the hash function is "k % 10", then in the chaining technique, both the nodes will be stored at the same position by creating a linked list. Even if there is some space in the hash table at some other index, we create a linked list and store the items into it. In the above example, the index "3" might be empty, so we can store "22" at index "3" but in chaining, we create one linked list and store "22" into it at index "2". So, there is not a proper utilization of space.

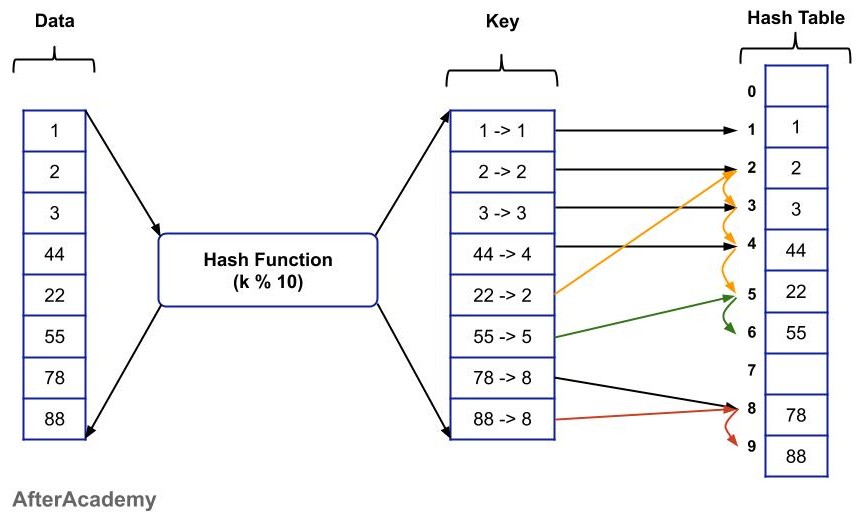
In the open addressing technique, we make efficient use of the space of the hash table. Following are the steps that are followed in open addressing:

• With the help of the hash function, we generate some keys and we go to the "kth" index to find if some value is already stored at that place or not.
• If the index is empty, then we can directly store the value at that index.
• If some value is already present in that place, then we start searching for the next available space and we store the value in the available space.

In this way, we can store the keys without using any extra pointer or without using any linked list.

Let's see how insertion, deletion, and searching can be performed in open addressing:

• Insertion: For inserting any value in the hash table, we find the key "k" with the help of some hash function and we go to the "kth" index and find if the place is empty or not. If it is empty then we directly insert the value and if the index is not empty then we search for the next available space and insert the value at the vacant position.
• Deletion: For deleting any element, enter the element in the hash function and get the key "k" from that and directly go to the kth index and find if the value is same as the one that you want to delete. If it is the same element, then delete the element and if the element is not the same, then traverse the hash table to find the element and once found, just delete it. Traverse until you encounter a space.

One thing that is to be noted in the deletion operation is that after deletion of some data from the hash table, you should denote the deleted node by some identifier because if proper identification is not there then during traversal you will stop traversing if you found some empty space because you will assume that there is no data after this place.

So, you must denote the deleted place with some identifier that will be used during traversing. So, that you can traverse even after the empty space created due to deletion.

• Searching: In order to search some value in the hash table, just enter the value to be searched in the hash function and get the key "k" from that and directly go to the "kth" index and find if the value is same as the one that you want to find. If it is the same element, then return the element and if the element is not the same, then traverse the hash table to find the element and once found, just return it. Traverse until you encounter space in the hash table.

Critical Ideas to think/Explore further

• We can use a hash table to solve several problems in programming. In such problems, the efficient implementation of insert, delete and search operations are mostly required for an efficient solution. We suggest learners to prepare a list of such problems and explore different patterns related to problem-solving.
• In a good hash function, your key should be uniformly distributed i.e. each key should be equally likely to hash to any slot in the Hash Table, independently where any other key has hashed to.
• Many real life applications required a dynamic data set that supports only the Dictionary operations: Insert, Search and Delete. In such a situation, the Hash Table in an effective data structure to implement dictionaries.
• We can take the benefit of the direct address table when we can afford an array that has one position for every possible key.
• We highly recommend learners to implement their own Hash Table with using separate chaining method. Let's try this in your favorite programming language!
• Compare the applications of Hash Table and BST. Also explore the situation where we prefer BST over Hash Table to organize the data.
• Understanding the design of different Hash Functions are important because here you will find beautiful mathematical pattern related to the distribution of the keys and order of storing of the data.
• If you want to learn further, then you can try to understand the idea of primary and secondary clustering in the case of the open addressing method.

Suggested Problems to solve in Hashing

• Check if two arrays are equal or not
• The intersection of two unsorted array
• Longest Consecutive Sequence
• Valid Anagram
• Majority Element
• Sort characters by frequency
• Triplet with 0 sum
• First missing positive
• Largest subarray with 0 sum
• Max points on the straight line

Happy Learning, Enjoy Algorithms!

Team AfterAcademy!