Stack and its basic Operations

What is stack?

First, let us see the properties of data structures that we already do know and build-up our concepts towards the stack.

Array: Its a random-access container, meaning any element of this container can be accessed instantly
Linked List: It's a sequential-access container, meaning that elements of this data structure can only be accessed sequentially

→ Following a similar definition, a stack is a container where only the top element can be accessed or operated upon.

A Stack is a data structure following the LIFO(Last In, First Out) principle.

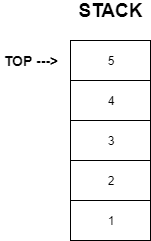
If you have trouble visualizing stacks, just assume a stack of books.

In a stack of books, you can only see the top book
If you want to access any other book, you would first need to remove the books on top of it
The bottom-most book in the stack was put first and can only be removed at the last after all books on top of it have been removed.

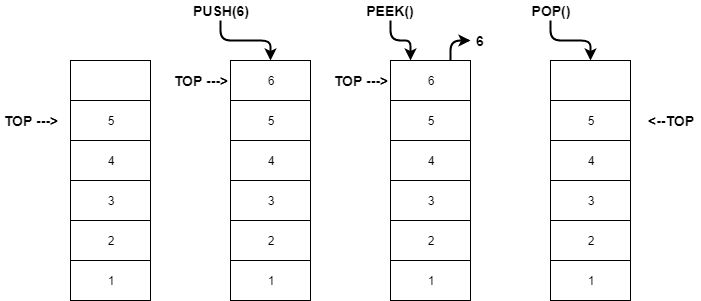
PUSH Operation

Push operation refers to inserting an element in the stack. Since there’s only one position at which the new element can be inserted — Top of the stack, the new element is inserted at the top of the stack.

POP Operation

Pop operation refers to the removal of an element. Again, since we only have access to the element at the top of the stack, there’s only one element that we can remove. We just remove the top of the stack. Note: We can also choose to return the value of the popped element back, its completely at the choice of the programmer to implement this.

PEEK Operation

Peek operation allows the user to see the element on the top of the stack. The stack is not modified in any manner in this operation.

isEmpty : Check if stack is empty or not

To prevent performing operations on an empty stack, the programmer is required to internally maintain the size of the stack which will be updated during push and pop operations accordingly. isEmpty() conventionally returns a boolean value: True if size is 0, else False.

Stack Implementation

As we’ve learned before, Stack is a very useful concept that a good programmer could use to his/her benefit. But can you implement it in your code yet? It's not that difficult once you think about it, let’s walk through its properties and implement them in code.

You should remember one very important thing though →

All operations in the stack must be of O(1) time complexity

We shall be implementing stack in two different ways by changing the underlying container: Array and Linked List.

1. Array Implementation

An array is one of the simplest containers offering random access to users based on indexes. But can we access any element of the stack at any given time? No . That’s why we need to set an index as top and then access only the element at index top.

int stack[10]
int top = -1

Here, 10 is a pre-defined capacity of the stack. We can throw a stack overflow error if a user tries to exceed this capacity.

★ The default value for the top is -1, denoting that the stack is empty.

Do we need to store any other parameter for the stack? current size, perhaps? No. We may need to store the capacity of the stack but we don’t need to store the current size. We can know the current size of stack by looking at the value of the top. (How?)

Let us wrap this group of data members in a class

class Stack{
    int arr[]
    int capacity
    int top
}

Let us also create a constructor which initializes capacity and top

Stack(int cap)
{
    capacity = cap
    top = -1
}

★ You are also required to allocate memory to arr according to the language you use to implement it.

→Now, we need to implement the operations that we generally perform on stacks.

PUSH Operation

What changes are made to the stack when a new element is pushed?

A new element is inserted on top
The value of top increases by 1

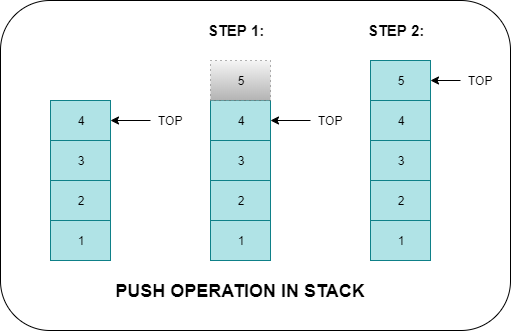
▹ What if the stack is filled to its capacity?

We shall check if the stack if full before inserting a new element and throw an error if it is.

Now, let us implement this simply

void push(int item)
{
    if ( top == capacity - 1 )
        print( "Stack overflow!" )
    else
    {
        arr[top+1] = item
        top = top + 1
    }
}

POP Operation

Let’s try one more: Pop().

What changes are made to the stack internally for a pop operation?

The top element is removed
The value of top is decreased by 1

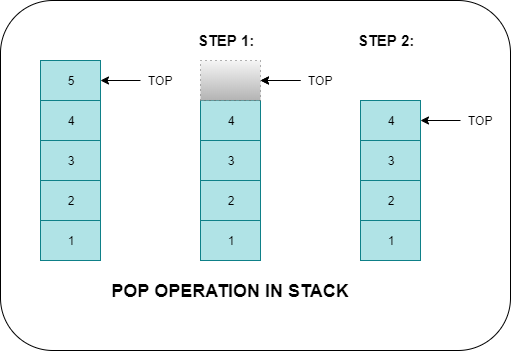
▹ Can you think of an exception in this case like the one above of stack being full? Ans: The stack can be empty when the pop operation is called

Let’s try implementing it now

void pop()
{
    if ( isEmpty() == True )
        print( "Stack is empty!" )
    else
        top = top - 1
}

★ Is decreasing the value of top same as deleting the top element? ( Think! )

Peek and isEmpty Operation

Peek and isEmpty are quite simple to implement. We need to steer clear of exceptions though.

int peek()
{
    if ( isEmpty() == True )
    {
        print( "Stack is empty!" )
        return -1
    }
    else 
        return arr[top]
}

bool isEmpty()
{
    if ( top == -1 )
        return True
    else
        return False
}

2. Linked List Implementation

Before implementing stack with a linked list, let us first try to visualize a stack as a linked list. There are two ends of a linked list: head and tail.

Which end do you think should represent the top of the stack? ( Think! )

The top of the stack should be represented by head because otherwise, we would not be able to implement the operations of the stack in O(1) time complexity.

Let us assume that we have used class for linked list

class ListNode{
    int val
    ListNode next
}

What should an empty stack look like if implemented with a linked list? Ans: Its head will point to NULL

ListNode head = NULL

Is there any benefit to implementing a stack as linked list compared to arrays? Ans: We do not need to mention the size of the stack beforehand.

→ Although, if you want to implement a limit to prevent excess use, you may need to encapsulate the class ListNode inside some other class along with a data member capacity .

class Stack{
    int capacity
    class ListNode{
        int val
        ListNode next
    }
}

We shall be using just using class ListNode below for simplicity.

→Let us move towards stack operations

PUSH Operation

The same properties hold as above with an added benefit that we need not worry about the stack being full

void push(int item)
{
    ListNode temp = ListNode(item)
    temp.next = head
    head = temp
}

POP Operation

Properties of linked list relaxed us from checking if the stack is full in push operation. Do they provide any relaxation for exceptions in pop operation? No. We still need to check if the stack is empty.

Since the top is represented by the head in this implementation. How do we delete the first element in a linked list?

Simple, we make the second element as the head.

void pop()
{
    if ( head == NULL )
        print ( "Stack is empty!" )
    else
        head = head.next
}

★ You may be required to deallocate the popped node to avoid memory leak according to your programming language's conventions.

Peek and isEmpty Operation

The implementation of these two operations is pretty simple and straight-forward in the linked list too.

int peek()
{
    if ( head == NULL )
    {
        print ( "Stack is empty!" )
        return -1
    }
    else
        return head.val
}

bool isEmpty()
{
    if ( head == NULL )
        return True
    else
        return False
}

Augmentations in Stack

You can augment the stack data structure according to your needs. You can implement some extra operations like:-

isFull(): tells you if the stack if filled to its capacity
The pop operation could return the element being deleted

★ A quite interesting augmentation that has been asked in many interviews asks you to implement a MinStack which holds all properties of a regular stack but also returns the minimum value in the stack. Since all stack operations are expected to be executed in constant time, you need to return the minimum element in the stack in O(1) time complexity.

Applications of Stack Data Structure

An "undo" mechanism in text editors
Forward and backward feature in web browsers
Check for balanced parentheses in an expression
Expression evaluation and syntax parsing
Backtracking . This is a process when you need to access the most recent data element in a series of elements. Think of a maze - how do you find a way from an entrance to an exit? Once you reach a dead end, you must backtrack. But backtrack to where? to the previous choice point. Therefore, at each choice point, you store on a stack all possible choices. Then backtracking simply means popping a next choice from the stack.
We use a stack for the Iterative implementation of several recursive programs like tree traversals, DFS traversal in a graph, etc.
For solving several problems in algorithms, we use a stack as the principle data structure with which they organize their information.
Memory management: Any modern computer environment uses a stack as the primary memory management model for a running program.