Spiral Order Traversal of a Matrix

Difficulty: Medium

Asked in: Amazon, Microsoft

Understanding the Problem

Problem Description: Given a 2-dimensional array or a matrix, we have to traverse the given matrix in spiral order. For better understanding of what a spiral order traversal looks like, have a look at the below given diagram: →

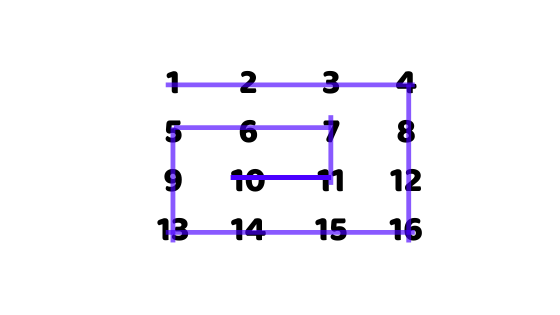
Input: A[][4]= 
               1  2  3  4
               5  6  7  8
               9  10 11 12
               13 14 15 16


Output: 1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10
Similarly, let's consider another example
Input: A[][4]=
              8  9  11 14
              16 21 20 24
              31 13 40 42
              52 70 30 34


Output: 8 9 11 14 24 42 34 30 70 52 31 16 21 20 40 13

Possible follow-up questions to ask the interviewer:-

• Can I to modify the given matrix?(Ans: No)

Solution by Iterative Approach

How would we do the spiral order traversal of the given matrix with a pen? We will start from the first row and first column and will continue drawing a spiral through the matrix.

Solution idea:

We will do the same traversal as discussed starting from the first row and column in all the four directions: →

• Left to Right
• Top to Bottom
• Right to Left and
• Bottom to Top

Solution steps

• We will use four loops to traverse in the four directions. Each loop for a single direction.
• Also, we will use four variables to indicate the start of the row index, end of the row index, the start of the column index and end of the column index.

Pseudo-Code

void spiralOrderTraversal(int end_row, int end_col, int A[R][C]) 
{ 
  int i
  int start_row = 0
  int start_col = 0
   
  while(start_row < end_row && start_col < end_col)
  {
      for(i = start_col to end_col-1; i=i+1)
      {
         print(A[start_row][i])
      }   
      start_row = start_row + 1
      
      for(i = start_row to end_row-1; i=i+1)
      {
         print(A[i][end_col - 1])
      }
      end_col = end_col - 1
      
      if(start_row < end_row)
      { 
        for(i = end_col-1 to start_col; i=i-1) 
           print(A[end_row-1][i])
        end_row = end_row - 1
      } 
    
      if(start_col < end_col) 
      { 
        for(i = end_row-1 to start_row; i=i-1) 
           print(A[i][start_col]
        start_col = start_col + 1
     } 
  } 
}

Complexity Analysis:

We are traversing and printing each element of the matrix once.

Time Complexity: O(R*C)(Here R refers to the number of rows and C refers to the number of columns in a matrix)

Space Complexity: O(1)

Solution by Recursive approach

We can solve the above problem with recursion following the similar approach by just printing the boundary of the matrix. In every recursive call, the size of the matrix is decreased and again the boundary of the newly small matrix with decreased dimension is printed.

Pseudo-Code

void spiralOrderTraversal(int A[R][C], int start_row, int start_col, int end_row, int end_col)
{
  if(start_row >= end_row || start_col >= end_col)
    return
  
  for(int i = start_row to end_col; i=i+1)
    print A[start_row][i]
  
  for(int i = start_row+1 to end_row; i=i+1)
    print A[i][end_col-1]
  
  if((end_row-1) != start_row)
  {
    for(int i = end_col-2 to start_col; i=i-1)
      print(A[end_row-1][i] 
  } 
  
  if((end_col-1) != start_col)
  {
    for(int i = end_row-2 to start_row; i=i-1)
      print(A[i][start_col] 
  }
  
 spiralOrderTraversal(A, start_row+1, start_col+1, end_row-1, end_col-1)
 
}

Critical ideas to think!

• Can you think of the time and space complexity of the recursive solution?(Hint: It is based on the same approach of traversing and printing each element.)

Suggested Problems to Solve

• Form a spiral matrix from a given array
• Print a matrix in reverse wave form
• Level Order Traversal in spiral form
• Print a matrix in a spiral form starting from a point
• Print a matrix in a reverse spiral form

Happy Coding! Enjoy Algorithm!!

AfterAcademy Data Structure And Algorithms Online Course - Admissions Open