Set Matrix Zeros - Interview Problem
AfterAcademy Tech
•
14 Nov 2019

Difficulty: Medium
Asked in: Amazon, Google
Understanding the Problem
Problem Description: Given a matrix, A of size M x N of 0's and 1's. If an element is 0, set its entire row and column to 0.
For Example:
Input:
[ [1, 0, 1],
[1, 1, 1],
[1, 1, 1] ]
Output:
[ [0, 0, 0],
[1, 0, 1],
[1, 0, 1] ]
Input:
[ [1, 0, 1],
[1, 1, 1],
[1, 0, 1] ]
Output:
[ [0, 0, 0],
[1, 0, 1],
[0, 0, 0] ]
Possible follow-up questions to ask the interviewer:-
- What are the constraints on the size of the matrix? (Ans: 1 ≤ N, M ≤ 1000)
- Do we need to change the rows and columns of elements which we set to zero? (Ans: No, only the zeroes present in the original matrix)
Solutions
We are discussing three ways to solve this problem:
- Brute Force Approach: Using nested loops and extra space
- Using Hash Table: Storing the status of rows and columns in the Hash Table.
- Using In-Place Hashing: Storing hash in the matrix’s first row and column.
1. Brute Force Approach
Common mistake
A simple solution that comes to mind for this problem is that we can traverse the matrix and for every ‘0’ we encounter, we update all values in its row and column to 0. This brute force solution seems quite easy but may actually lead to a wrong answer. (How? Think!)
Correct Solution idea
One way would be to create an auxiliary matrix of the same size filled with 1’s. We could make all changes required in this auxiliary matrix and then copy it to the original matrix in the end. We search for zeroes in the original matrix and update rows and columns in the auxiliary matrix.
Solution Steps
- First, create a temporary matrix of the same size M x N and initialize its all places with 1.
- Now scan the original matrix and if A[i][j] == 0 then set all the positions of row i and col j with 0 in new matrix.
- Copy all elements from the temporary matrix to the original matrix.
Pseudo-Code
void setMatrixZeros(int A[][], int M, int N)
{
int temp[M][N]
for (i = 0 to M-1)
for (j = 0 to N-1)
temp[i][j] = 1
for(i = 0 to M - 1)
{
for (j = 0 to N - 1)
{
if (A[i][j] == 0)
{
for (k = 0 to M - 1)
temp[k][j] = 0
for (k = 0 to N - 1)
temp[i][k] = 0
}
}
}
for (i = 0 to M-1)
for (j = 0 to N-1)
arr[i][j] = temp[i][j]
}
Complexity Analysis
For every cell, we are traversing its row and column and there are a total of N*M cells.
Time Complexity: O(N*M*(N+M)) (Think!)
Space Complexity: O(N*M), for storing the auxiliary matrix.
Critical ideas to think!
- How could we implement it in place in order to optimize space complexity?
- How can we reduce the time complexity of the solution?
2. Using Hash Table
Instead of using an auxiliary matrix, we could just store the rows and columns which need to be updated (Think!).
We could use a Hash Table to do so. We shall create a hash table for all rows and columns and set them to false. If the value of any row or column in hash is later updated to true, it's a signal for us to update that particular row or column’s value to 0.
Solution Steps
- Create 2 Hash Tables row and col respectively of size M and N.
- Now initialize all the values of row[] and col[] to false.
- Now iterate over the matrix and for every A[i][j] == 0, set row[i] = true and col[j] = true.
- After completion of step 3, again iterate through matrix A and for any A[i][j], if row[i] or col[j] is true then update A[i][j] to 0.
Pseudo Code
void setMatrixZeros(int A[][], int M, int N)
{
bool row[M], col[N]
for(i = 0 to M-1)
row[i] = false
for(j = 0 to N-1)
col[j] = false
for(i = 0 to M-1)
{
for(j = 0 to N-1)
{
if(A[i][j] == 0)
{
row[i] = true
col[j] = true
}
}
}
for(i = 0 to M-1)
{
for(j = 0 to N-1)
{
if(row[i] == true or col[j] == true)
A[i][j] = 0
}
}
}
Complexity Analysis
Time Complexity: Creating and filling values in 2 Hash Tables + Traversing the matrix + Updating the matrix
= O(N+M) + O(N*M) + O(N*M)
= O(N*M)
Space Complexity: O(M + N), for storing hash tables.
Critical ideas to think!
- How can we optimize the space complexity?
- What other matrix problems could be solved using a similar type of hashing approach?
3. Using In-Place Hashing
We are using extra space to store Hash Tables of rows and columns. We can optimize this space by trying to store hash for row and column in the matrix itself. (How?)
We can use the first row and first column of the matrix to store the status of the rows and columns respectively. The problem will occur for the status of first row and column which can be handled using two variables which will store the status of the first row and column (Think!)
Solution Steps
- Initialize firstRow and firstCol to false. These two variables will store the status of the first row and first column.
- Now use the first row and first column as your hash which stores the status of that row and column.
- Now iterate over the matrix and for every A[i][j] == 0, set A[i][0] = 0 and col[0][j] = 0.
- Now update the values of the matrix except first row and first column to 0 if A[i][0] = true or A[0][i] = true for A[i][j].
- Now update the values of the first row and first column.
void setMatrixZeros(int A[][], int M, int N)
{
for(j = 0 to N-1)
if(A[0][j] == 0)
firstRow = true
for(i = 0 to M-1)
if(A[i][0] == 0)
firstCol = true
for(i = 0 to M-1)
{
for(j = 0 to N-1)
{
if(A[i][j] == 0)
{
A[i][0] = 0
A[0][j] = 0
}
}
}
for (i = 1 to M-1)
{
for (j = 1 to N-1)
{
if(A[0][j] == 0 || A[i][0] == 0)
A[i][j] = 0
}
}
if(firstRow == true)
{
for( i = 0 to N-1 )
A[0][i] = 0
}
if(firstCol == true)
{
for(i = 0 to M-1)
A[i][0] = 0
}
}
Complexity Analysis
Time Complexity: Checking the first row and first column + Traversing and updating the matrix + Updating first row and first column.
= O(M) + O(N) + O(M*N) + O(M) + O(N)
= O(M*N)
Space Complexity: O(1)
Critical ideas to think!
- Why are the first row and first column updated separately?
- Can you use other data structures to efficiently solve this problem?
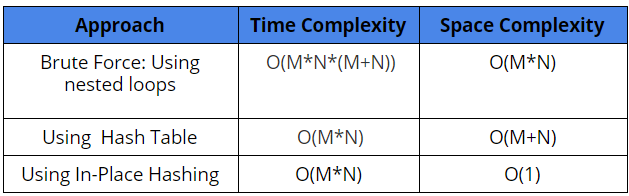
Comparison of different solutions
Suggested problems to solve
- Given a boolean matrix, find k such that all elements in the kth row are 0 and all elements in the kth column are 1
- Print unique rows in a given Boolean matrix
- Check if matrix can be converted to another matrix by transposing square sub-matrices
- Print a given matrix in spiral form
- Rotate a matrix by 90 degree
If you have any more approaches or you find an error/bug in the above solutions, please comment down below.
Happy Coding! Enjoy Algorithms!
AfterAcademy Data Structure And Algorithms Online Course - Admissions Open
Written by AfterAcademy Tech
Share this article and spread the knowledge
Read Similar Articles
AfterAcademy Tech
Median in a Row-wise Sorted Matrix-Interview Problem
The problem is to find the median in a row-wise sorted matrix. This is an interview problem asked in companies like Amazon. There is a further constraints on extra space. We have discussed two possible solutions.

AfterAcademy Tech
Move all the zeroes to the end - Interview Problem
Given an array A[] of n elements filled with several integers, some of them being zeroes, you need to move all the zeroes to the end.

AfterAcademy Tech
Greatest Common Divisor-Interview Problem
This is a mathematical problem asked in interviews of Google like companies. For solving such problems you need to have some math skills and also some idea of algorithms like Euclid's GCD algorithm.

AfterAcademy Tech
Remove Duplicates in a Sorted Array-Interview Problem
This is an interview problem asked in companies like Google, Microsoft, Amazon. The problem is to remove duplicates from a sorted array or list.