Minimum Depth of Binary Tree - Interview Problem

Min Depth of Binary Tree

Difficulty : Easy

Asked in : Facebook, Amazon

Understanding the problem

Problem description: Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

NOTE: The path has to end on a leaf node.

Example:

Input:

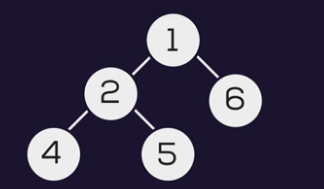
output : 2

Explanation: The minimum depth is 2 through the path from root node 1 to leaf node 6.

The node structure for the BST passed to your function will be

class TreeNode
{
    int val
    TreeNode left
    TreeNode right
}

Solutions

We are discussing two approaches to solve this problem:

Recursive solution: Solve the problem by calculating the minimum depth of left and right subtree recursively.
Using Level order traversal: Perform level traversal and return the depth of the first encountered leaf node.

1. Recursive solution

The steps to be followed are:

Check if the node is a leaf node or not. If it is a leaf node then return 1.
If the left child is NULL then recur to the right child or if the right child is NULL then recur to the left child.
If both the children are not NULL then return the minimum of both heights of left and right sub-tree + 1.

This is a Depth First Search(DFS) approach of solving tree problem.

Pseudo code

int findMinDepth(TreeNode root)
{
    if(root == NULL)
       return 0
    if(root.left == NULL and root.right == NULL)
       return 1
    if(root.left == NULL)
       return 1 + findMinDepth(root.right)
    if(root.right == NULL)
       return 1 + findMinDepth(root.left) 
    return 1 + min(findMinDepth(root.left), findMinDepth(root.right))
}

Complexity Analysis

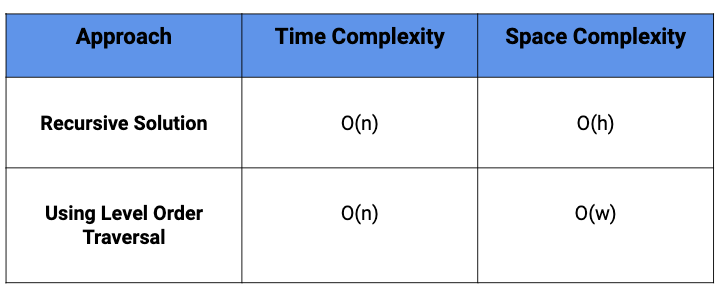
In the above approach, we are traversing each node of the tree only once. Time complexity : O(n)

Space Complexity of recursive algorithm is proportional to the maximum depth of recursion tree generated which is equal to the height of the tree (h). Space complexity : O(h) for recursion call stack.

Critical ideas to think

What is the space complexity in the worst and best-case scenario?
Is there some other way to solve this problem recursively?
Why recursion help us to solve the tree problems easily? Explore the properties of Pre-order, In-Order and Post-Order traversal.

2. Level order Traversal

Level order traversal is the Breadth-First Traversal of the tree where we traverse the tree by accessing the nodes in level by level fashion. For each node, the first node is visited and then it’s child nodes are put in a FIFO queue.

The recursive approach may end up with a complete traversal of Binary Tree even when the topmost leaf is close to root. So we can design a better solution by using the idea of Level Order Traversal. While doing level order traversal, we will return the depth of the first encountered leaf node and return its level.

In the above example:- 1 is the root node is considered at the first level, 2 and 6 at the second level, 4 and 5 at the third level.

Pseudo Code

class TreeNode 
{ 
    int data
    TreeNode left
    TreeNode right
}

class QueueItem
{
    TreeNode node
    int depth
}
int findMinDepth(TreeNode root)
{
    if (root is NULL)
        return 0
    else 
    {
        // Queue of type QueueItem
        Queue Q 
        QueueItem QI = {root, 1}
        Q.enqueue(QI)
        while(Q is not empty)
        {
            QI = Q.dequeue()
            TreeNode subroot = QI.node
            int depth = QI.depth
            //If the first leaf node is seen, then return depth
            if (subroot.left == NULL and subroot.right == NULL)
                return depth
            else 
            {
                if(subroot.left != NULL)
                {
                    QI.node = subroot.left
                    QI.depth = depth + 1
                    Q.enqueue(QI)
                }
                if(subroot.right is != NULL){
                    QI.node = subroot.right
                    QI.depth = depth + 1
                    Q.push(QI)
                }
            }
        }
    }
    return 0
}

Complexity Analysis

From the FIFO queue, Each item get inserted and deleted only once. Total number of queue operations = 2n.

Time complexity = O(n), where n is the total number of nodes.

Level order traversal require space proportional to the max width of the tree (w) which is equal ot the maximum number of nodes at a given level. Space Complexity = O(w) (Think!)

Critical Ideas to think

Why we Queue data structure in the level order traversal?
What is worst and best-case scenario of space complexity?
Can we write a recursive code for level order traversal? If yes then, compare its performace with Iterative Implementation (level order traversal using queue).