Merge Sort

Sorting is a process of arranging items systematically. There are several ways to sort a list of items, you may read about some of the basic algorithms we have discussed here.

Understanding the problem

Given an array of integers A[] , Write a program to sort the array in ascending order using Merge Sort.

Example 1 

Input: A[] = [5,2,3,1]
Output: [1,2,3,5]

Example 2 

Input: A[] = [8,7,4,2,9,1,5,6]
Output: [1,2,4,5,6,7,8,9]

The given constraint is that the input array A[] could be of length 10⁶.

In Merge Sort, we divide the whole problem or array into two halves and again we divide the halves into two halves and so on. At last, we sort the array and then combine the halves to get the sorted array. So, basically, we divide and conquer. For example,

The visualization of Example 2, using merge sort:

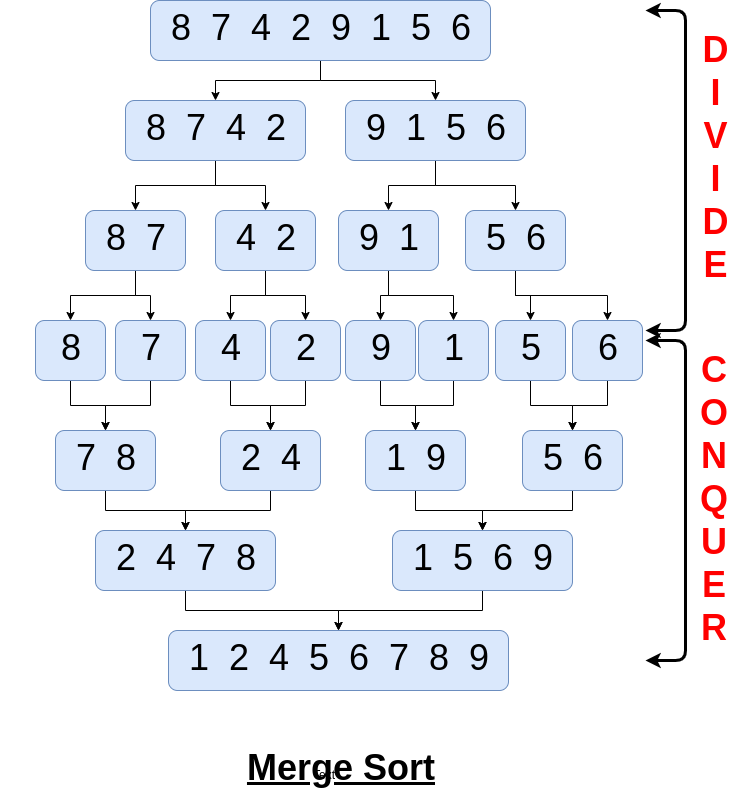
Before moving forward, if you don't know divide and conquer, then understand about divide and conquer from here.

Why Merge Sort?

Merge Sort is a stable sort which means that the same element in an array maintain their original positions with respect to each other. Its time complexity is considered to be of O(n log n) in case of best, average and worst cases. Let’s see how the O( n log n ) running time affects the actual execution time.

Let’s say that a quadratic sorting algorithm takes approximately n²/10⁶ seconds to sort n values. When n = 100, then running time is 100²/10⁶ = 1/100 sec. When n = 1000 then 1000²/10⁶ = 1. If the size of the array grew by a factor of 10 then the running time will increase 100 times, i.e. 100 secs, That means, quadratic sorting algorithms could take a large amount of time to sort arrays of length 10⁴ or more.

In case of merge sort, the time required to sort 10⁴ sized array could take O(10⁴ log 10⁴) / 10⁶ ~ less than 0.1 secs. So you can observe the significant amount of time difference between the two sorting algorithms.

Working of merge sort

This sorting approach uses Divide and Conquer, so we need to figure out how our subproblems will look like. Think of subproblem as sorting the subarray starting at index left and going through the index right. Here’s how merge sort uses divide-and-conquer:

  1. Divide — We will divide the array into two sub-arrays and will try to sort them.
  2. Conquer — We recursively sort the two subarray of approximately n /2, elements each, takes some amount of time, but we’ll account for that time when we consider the subproblems.
  3. Combine — Considering the two sub-arrays to be sorted, we will try to merge them in O(n)

Now, to sort the input array using the merge sort, we will have to identify the base case. If we take two pointers left and right pointing to the first and last index of input array respectively, then the base case would be the scenario when the left pointer is equal to the right pointer or in other words, when the size of the array is equal to 1.

A subarray with no elements or just one element is already sorted. So we’ll divide-conquer-combine only when left < right .

If the base case is not true, then that means we will have to divide the array into subarrays. So, we will find the midpoint of the array by using the formula mid = (left + right)/2 . We will then divide the array into further subarrays recursively. Now combine the divided subarrays by considering that the two sorted arrays subarrays after merging should result in the sorted array in linear time.

It’s the combining step when you have to merge two sorted subarrays, there the real work happens.

So, the final piece is the merge function. In order to merge the sorted subarrays A[left to mid] and A[mid to right] and have the result in A[left to right] , we first need to make temporary arrays and copy A[left to mid] and A[mid to right] into these temporary arrays, let's name them leftArr and rightArr . We should put the smallest of the two subarrays into A[left] . Because the subarrays are sorted, the smallest value must be in one of just two places: either leftArr[0] or rightArr[0] and we put the smaller one into A[left] . We will go on finding the smaller one and putting it into the array, in this way we will be left with sorted A[left to right] .

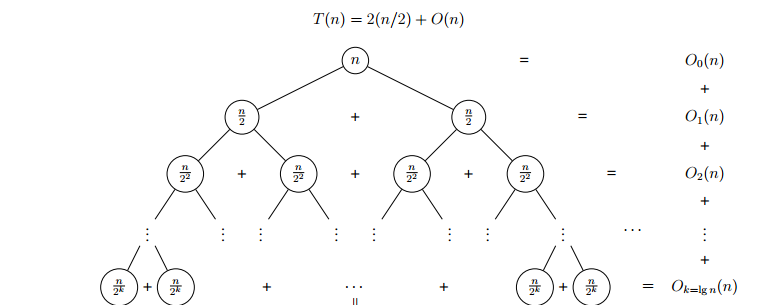
For an n-sized array, the recursion tree will look like →

Let's go through the above example A[] = [8, 7, 4, 2, 9, 1, 5, 6] to understand it well.

Initially, the left pointer is set to the 0th index and the right pointer is set to the 7th index.

  • Divide A[0 to 7] into A[0 to 3] and A[4 to 7] which could further be divided into A[0 to 1], A[2 to 3] and A[4 to 5] and A[6 to 7], and so on.
  • The conquer step is to sort the two subarrays A[0 to 3] , which contains [8, 7, 4, 2] , and A[4 to 7] , which contains [9, 1, 5, 6] . When we come back from the conquer step, each of the two subarrays is sorted: A[0 to 3] contains [2, 4, 7, 8] and A[4 to 7] contains [1, 5, 6, 9] .
  • The Combine step merges the two sorted subarrays, producing the final sorted array [1, 2, 4, 5, 6, 7, 8, 9] .
Algorithm
  • Divide the unsorted list into N sublists, each containing 1 element.
  • Take adjacent pairs of two singleton lists and merge them to form a list of 2 elements. N will now convert into N/2 lists of size 2.
  • Repeat the process till a single sorted list of obtained.
Pseudo Code 
// function to combine A[left to mid] and A[mid+1 to right]
void merge(int A[], int left, int mid, int right){
    int n1 = mid - left + 1
    int n2 = right - mid
    int X[n1]
    int Y[n2]
    for(int i = 0 to n1){
        X[i] = A[left + i]
    }
    for(int j = 0 to n1){
        Y[i] = A[mid + 1 + i]
    }
    int i = 0, j = 0, k = l
    while(i < n1 and j < n2){
        if(X[i] > Y[j]){
            A[k] = Y[j]
            j = j + 1
        } else {
            A[k] = X[i]
            i = i + 1
        }
        k = k + 1
    }
    while(i < n1){
        A[k] = X[i]
        i = i + 1
        k = k + 1
    }
    while(j < n2){
        A[k] = Y[j]
        j = j + 1
        k = k + 1
    }
}
// Utility function to sort the array A from left idx to right idx
void mergeSortUtil(int A[], int left, int right){
    // base case
    if(left == right)
        return
    // divide
    int mid = (left + right) / 2
    // solving(conquer)
    mergeSortUtil(A, left, mid) 
    mergeSortUtil(A, mid + 1, right)  
    // Combine
    merge(A, left, mid, right)    
}
// Driver function
void mergeSort(int A[], int size){
    mergeSortUtil(A, 0, size)
}
Complexity Analysis

If the running time of merge sort for a list of length n is T ( n ), then the recurrence T ( n ) = 2 T ( n /2) + n

So, sorting n objects, merge sort has an average and worst-case performance of O ( n log n ).

Space complexity — if you count stack frames, then it’s O(n)+ O(log n), so asymptotically its O(n).

Critical ideas to Think
  • Identify the scenario when the subproblems cannot be divided further.
  • How does the merging of two sorted arrays performed here?
  • For an n-sized array, how many times will the divide take place?
  • How the time complexity of merge function is O(n)?
  • Do you think that there could be a better point to divide the array into subarrays instead of dividing it in the middle? If no, Why?

You may now solve this sorting algorithm from here for practice.

Please comment down below if you have a better insight in the above approach.

Happy Coding, Enjoy Algorithms!