Longest Common Prefix

Difficulty: Hard

Asked in: Amazon, Google

Understanding the problem

Problem Description

Given the array of strings S , write a program to find the longest common prefix string which is the prefix of all the strings in the array.

Problem Note

The longest common prefix for a pair of strings S1 and S2 is the longest string which is the prefix of both S1 and S2.
All given inputs are in lowercase letters a-z.
If there is no common prefix, return "-1" .

Example 1

Input: S[] = [“apple", "ape", "april”] 
Output: "ap"

Example 2

Input: S[] = ["flower","flow","flight"] 
Output: "fl"

Example 3

Input: S[] = [“after”, ”academy, ”mindorks”] 
Output: “-1” 
Explanation: There is no common prefix among the input strings.

Solutions

We will be discussing four different approaches to solve this problem

Horizontal Scanning — Find the LCP of strs[0] with strs[1] with strs[2] and so on.
Vertical Scanning — Scan all the characters at index 0 then index 1 then index 2 and so on.
Divide and Conquer — Divide the strs array to two parts and merge the LCP of both the subparts.
Binary Search — Compare the substrings[0 to mid] of the smallest string with each string and keep on updating front and behind accordingly.

1. Horizontal Scanning

A simple way to find the longest common prefix shared by a set of strings LCP ( S 1… Sn ) could be found under the observation that
LCP ( S 1… Sn ) = LCP ( LCP ( LCP ( S 1, S 2), S 3), …. Sn )

To achieve it, simply iterate through the strings [ S 1… Sn ], finding at each iteration i the longest common prefix of strings LCP ( S 1… Si ). When the LCP ( S 1… Si ) is an empty string, then you can return an empty string. Otherwise, after n iterations, the algorithm will returns LCP ( S 1… Sn ).

Solution steps

take a variable prefix and initialize it with strs[0]
compare the prefix of each string in the strs array with the prefix variable and update the prefix accordingly
if at any point length of prefix becomes 0 then return -1
return prefix after comparing with each string of the strs array

Pseudo Code

string longestCommonPrefix(string[] strs, int size) {
    if (size == 0) 
        return "-1"
    string prefix = strs[0]
    for (int i = 1 to size)
        while (strs[i].indexOf(prefix) != 0) {
            prefix = prefix.substring(0, prefix.length() - 1)
            if (prefix.isEmpty()) 
                return "-1"
        }
    return prefix
}

Complexity Analysis

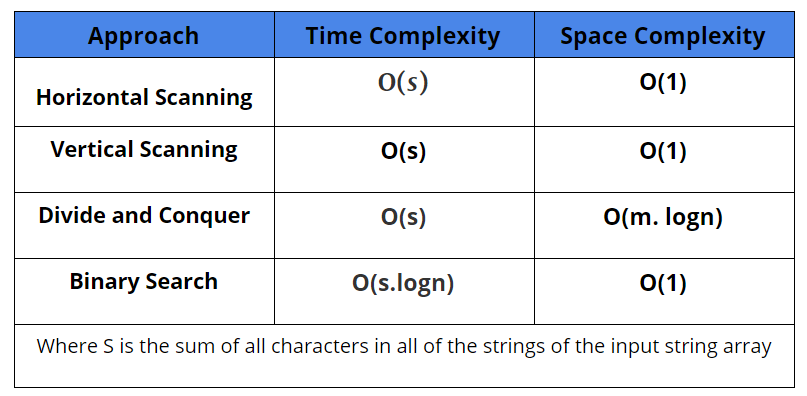
Time complexity: O ( S ), where S is the sum of all characters in all strings.

Space complexity: O (1).

Critical Ideas to Think

Do you think that if all the strings in the array would be same then it would be the worst-case for this approach? If yes, Why?
What does the prefix.substring(0, prefix.length() -1) mean?
What is the initial value of prefix the variable and why?
Can you think of any other approach?

2. Vertical scanning

Imagine a very short string is the common prefix of the array. The above approach will still do S comparisons. One way to optimize this case is to do vertical scanning. We compare characters from top to bottom on the same column (same character index of the strings) before moving on to the next column.

Example —

[
"AfterAcademy",
"AfterLife",
"Affirmative",
"Adjective",
]

Vertically scan the 0th index of all the strings, in this case its "A" for each string so the LCP till now is "A". Now vertically scan the 1st index of each string, the second character for each string are not same, so we will return the prefix till now.

Solution Step

Start comparing the ith character for each string, if all the character for ith position are all same, then add it to the prefix, otherwise, return prefix till now.

Pseudo Code

string longestCommonPrefix(String[] strs, int size) {
    if (strs.length == 0) 
        return "-1"
    for (int i = 0 to i < strs[0].length()){
        char c = strs[0][i]
        for (int j = 1 to j < strs.length) {
            if (i == strs[j].length() or strs[j][i] != c)
                return strs[0].substring(0, i)
        }
    }
    return strs[0]
}

Complexity Analysis

Time complexity : O ( S ), where S is the sum of all characters in all strings.

In the best case there are at most n * minLen comparisons where minLen is the length of the shortest string in the array.

Space complexity : O (1). We only used constant extra space.

Critical Ideas to Think

Do you think the worst case for this approach is exactly the same as in the horizontal scanning?
Why we are returning strs[0] at the end of the function in pseudocode?

3: Divide and conquer

The thought of this algorithm is related to the associative property of LCP operation. Notice that: LCP ( S 1… Sn ) = LCP ( LCP ( S 1… Sk ), LCP ( Sk +1… Sn )) , where LCP ( S 1… Sn ) is the longest common prefix in the set of strings [ S 1… Sn ] , 1 < k < n1 < k < n

Thus, the divide and conquer approach could be implied here by dividing the LCP(Si…Sj) problem into two subproblems LCP ( Si … Smid ) and LCP ( Smid +1… Sj ) , where mid is the middle of the Si and Sj .

We can keep on dividing the problems into two subproblems until they cannot be divided further.

Now to conquer the solution, we compare the solutions of the two subproblems till there is no character match at each level. The found common prefix would be the solution of LCP(Si…Sj) .

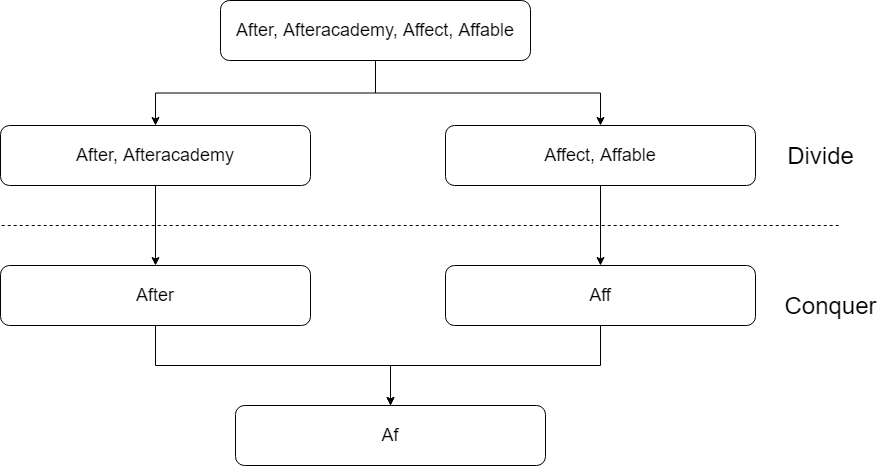
Solution Steps

Recursively divide the strs array into two sub-arrays.
In the conquer step, merge the result of the two sub-arrays which will be LCP(LCP(strs[left…mid], LCP([mid+1…right])) and return it.

Pseudo Code

string longestCommonPrefix(string[] strs, int size) {
    if (size == 0) return "-1"
        return longestCommonPrefixutil(strs, 0 , size - 1)
}

string longestCommonPrefixutil(string[] strs, int left, int right) {
    if (left == right) {
        return strs[left]
    }
    else {
        int mid = (left + right)/2;
        string left_lcp =   longestCommonPrefixutil(strs, left , mid)
        string right_lcp =  longestCommonPrefixutil(strs, mid + 1,right)
        return commonPrefix(left_lcp, right_lcp)
   }
}

string commonPrefix(String left, String right) {
    int smaller = min(left.length(), right.length())
    for (int i = 0 to i < smaller) {
        if ( left[i] != right[i] )
            return left.substring(0, i)
    }
    return left.substring(0, smaller)
}

Complexity Analysis

Time complexity : O ( S ), where S is the number of all characters in the array.

Space complexity : O ( m ⋅ log n ) (Why?)

There are log n recursive calls and each store need m space to store the result

Critical ideas to think

How we are dividing the problems set to subproblems?
Do you think divide and conquer is similar to horizontal scanning?
Do you think that the best case complexity will be O(minLen*n) ?
What does the commonPrefix function do?

4: Binary search

The idea is to apply a binary search method to find the string with maximum value L , which is the common prefix of all of the strings. The algorithm searches space is the interval (0… minLen ), where minLen is minimum string length and the maximum possible common prefix. Each time the search space is divided into two equal parts, one of them is discarded because it is sure that it doesn't contain the solution. There are two possible cases: S[1...mid] is not a common string. This means that for each j > i, S[1..j] is not a common string and we discard the second half of the search space. S[1...mid] is a common string. This means that for each i < j, S[1..i] is a common string and we discard the first half of the search space because we try to find a longer common prefix.

Solution steps

Pick the smallest string
Take variable front = 0 and behind = len(smallest string)
Do binary search

Compare the substring up to middle character of the smallest string with every other string at that index.
if all the strings have the same substring(0, mid) then move front to mid + 1 else move behind to mid-1 .
If front becomes equal to behind then return the strs[0].substring(0, mid)

Pseudo Code

string longestCommonPrefix(string[] strs, int size) {
    if(size==0)
        return "-1"
    minLen=INT_MAX
    for(i = 0 to i < size){
        minLen = min(minLen,strs[i].length())
    }
    front = 1
    behind = minLen

    prefix = ""
    while(front <= behind) {
        mid = (front+behind)/2
        string temp=strs[0].substring(0, mid)
        int j = 1
        for(j=1 to j < size) {
           if(!strs[j].startsWith(temp)) {
                behind = mid-1
                break
            }
        }
        if(j==strs.length){

            prefix = temp
            front=mid+1 
        }
    }
    return prefix
}

Complexity Analysis

Time complexity : O ( S ⋅log n ), where S is the sum of all characters in all strings

Space complexity : O (1)

Critical Ideas to Think

Do you think that the binary search approach is not better than the approaches described above?
Why we are comparing substrings(0 to mid) instead of comparing only the middle character of every other string in the strs array? Can you think of a case in this scenario when we will compare only the mid character?
Why did we start this algorithm by finding the minLen?
Do you think that the best case and average case are the same in the binary search approach?
Can you take some example and compare the time complexity of each of the approaches described above.