Flatten Binary Tree to Linked List

Flatten Binary tree to Linked List

Asked in: Amazon, Microsoft, Adobe

Difficulty: Medium

Understanding the Problem

Problem Description: Given a binary tree, flatten it to a linked list in-place. After flattening, the left of each node should point to NULL and right should contain the next node in pre-order so that it resembles a singly linked list.

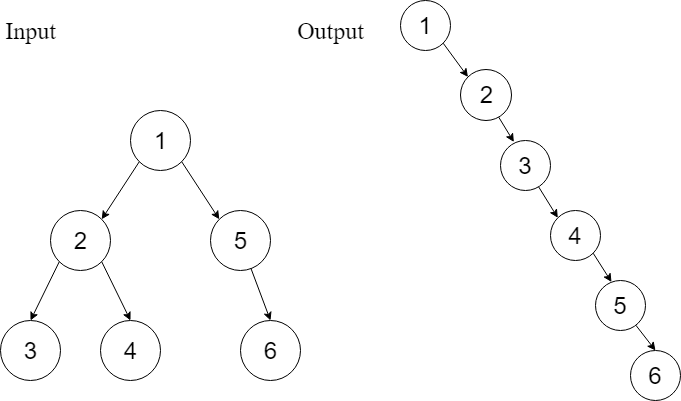
Example 1

Example 2

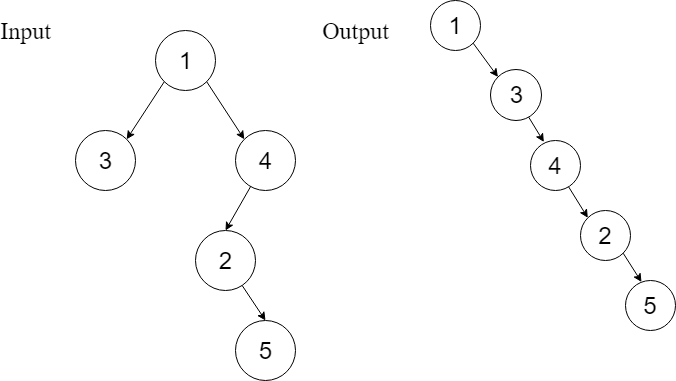
By looking at the example shown, it is very obvious that the head of the output linked list is the root of the tree node, followed by a flattened left subtree, which is followed by a flattened right subtree.

The node structure passed to your function will be

class TreeNode
{
    int data
    TreeNode left
    TreeNode right
}

Possible follow up questions to ask the interviewer —

Can I use extra space? ( Ans : You can but try to optimize if possible.)
What to return if we are given an empty tree? ( Ans : Just return null in this case.)

Hint → If you notice carefully in the flattened tree, each node’s right child points to the next node of a pre-order traversal.

Solutions

We will see three different approaches to solve this problem →

Reverse preorder traversal — Recursively flatten the right and left children and concatenate them.
Iterative using Stack — Find the right-most leaf of the current left subtree, and append the subtree there.
Iterative without using auxiliary space — use while-loop to find the right-most leaf of the current left subtree and append it to the root’s right.

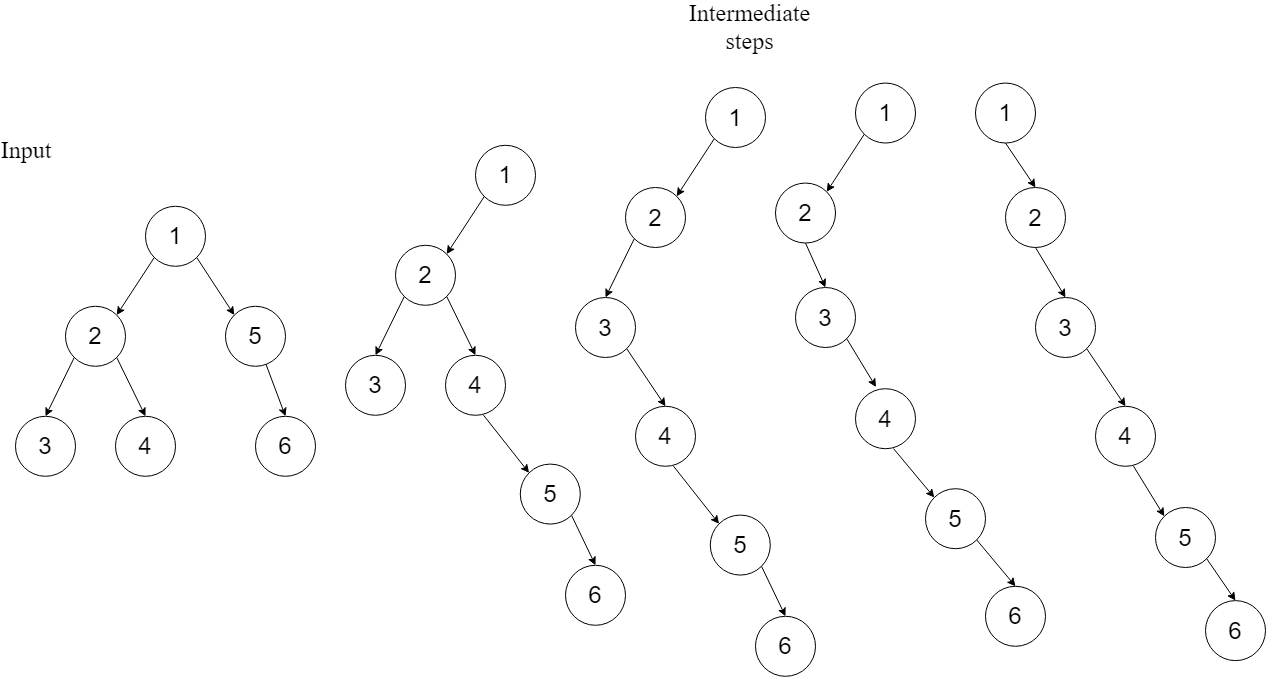
1. Reverse Preorder traversal

If you observe how the tree gets flatten then it is clear that for each subtree’s root node

Root’s left tree became the right tree
New right tree’s rightmost node points to root’s right tree

Solution steps —

Process right sub-tree
Process left sub-tree
Process root

Make the left node as a right node of the root
Set right node as a right node of the new right sub-tree
Set left node to NULL

Pseudo Code

void flatten(TreeNode root) 
{
    // reference temporary variable
    TreeNode temp = {0, NULL, NULL}
    reverse_preorder(root, temp);
    delete temp
}
void reverse_preorder(TreeNode root, TreeNode &temp) 
{
    if(root is NULL)
        return
    // process right sub-tree
    reverse_preorder(root.right, temp)
    // process left sub-tree
    reverse_preorder(root.left, temp)
    // set the right child of root with the left flattened tree
    root.right = temp
    // set the left child with null
    root.left = NULL
    // set the temp variable with the current node
    temp = root
}

Complexity analysis

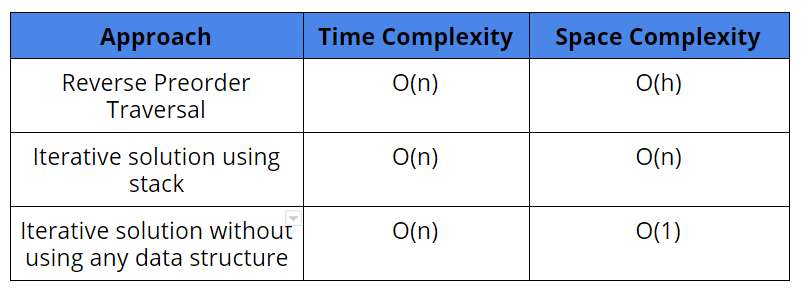
Time Complexity: O(n) Each node is visited exactly once and the operation performed on each node is of constant time.

Space Complexity: O(h) , where h is the height of the tree

Critical ideas to think

Why we used a reversed preorder approach instead of preorder?
Why the temporary TreeNode is passed in reference?
How did we set the right child of root with the left flattened tree?

2. Iterative Solution using Stack

The recursive solution could be solved iteratively using stack where at any instant the top of the stack will represent the root of a subtree.

Solution steps —

Check if the root is not NULL
Create a stack and push the root node to it and iterative the below steps until the stack is empty

pop the top node from the stack
push its right child and then its left child
peek the top node and set it to the right of the popped node
set the popped node’s left child as NULL

Pseudo Code

void flatten(TreeNode root) 
{
    if(root is NULL)
        return
    stack S
    S.push(root)
    while(S is not empty)
    {
        TreeNode subroot = S.pop()
        
        if(subroot.right)
            S.push(subroot.right)
        if(subroot.left)
            S.push(subroot.left)
            
        if(S is not empty)
            subroot.right = S.peek()
        subroot.left = null
    }
}

Complexity Analysis

Time Complexity: O(n)

Space Complexity: O(n)

Critical ideas to think

Why do we check if the stack is empty or not before assigning value to subroot.right?
Does this approach seem analogous to any famous approach?
Why do we push the right child and then the left child to the stack?
Can we optimize the space complexity in the iterative solution?

3. Iterative Without using any other data structure

Each time when we prune a right subtree, we use a while-loop to find the right-most leaf of the current left subtree and append the subtree there.

Pseudo Code

void flatten(TreeNode root) 
{
    TreeNode cur = root
    while (cur != null)
    {  
        if (cur.left != null)
        {
            // if we need to prune a right subtree
            if (cur.right != null)
            {
                TreeNode next = cur.left
                while (next.right != null)
                    next = next.right
                next.right = cur.right
            }
            cur.right = cur.left
            cur.left = null
        }  
        cur = cur.right
    }
}

Complexity Analysis

Visit each node at most twice (one for flattening and one for looking for rightmost leaf) and then for each node, cut the right tree and append it to its rightmost node. Overall, access to each node is in constant time.

Time Complexity: O(n)

Space Complexity: O(1)