Find Diameter of Binary Tree

Difficulty: Medium

Asked in: Facebook, Google, Amazon

Understanding the Problem

Problem Description

Given a binary tree, you need to compute the length of the diameter of the tree.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

Example:

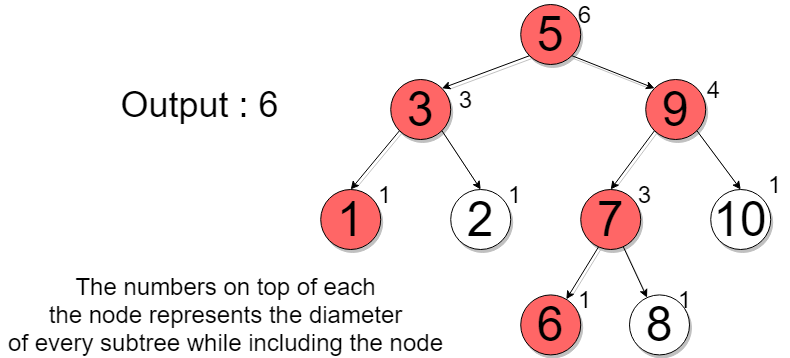
The node structure passed to your function will be

class TreeNode
{
    int data
    TreeNode left
    TreeNode right
}

You may first try to solve the problem here.

Solution

Recursive Approach — Return the maximum of left height + right height + 1 for each node of the subtree.
Iterative Approach — Make a post-order traversal using stack and keep track of the heights of each node with the help of a hash map.

1. Recursive approach

There exist two cases, the diameter of every subtree tree may include the sub-root or may not include the sub-root. The diameter of the sub-tree is certainly the maximum sum of the left height and the right height for a sub-root node.

Let’s calculate the depth of a tree for a root TreeNode . The Maximum Depth of Binary Tree problem has a solution that shows how to do this.

If at a root node (without using parents), the diameter is the maximum of either:

Max depth for Left Subtree + max depth for right subtree
The diameter of Left subtree (without using this sub root TreeNode )
The diameter of Right subtree (without using this sub root TreeNode )

We visit every TreeNode recursively and calculate (1), saving the largest value we've found in max . Since we calculate this value for every TreeNode , we have indirectly calculated (2) and (3) as well. Our solution is the final value for max .

Visualization

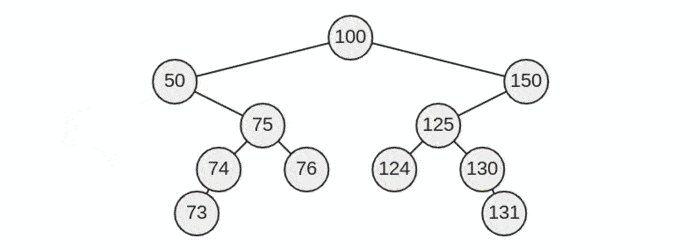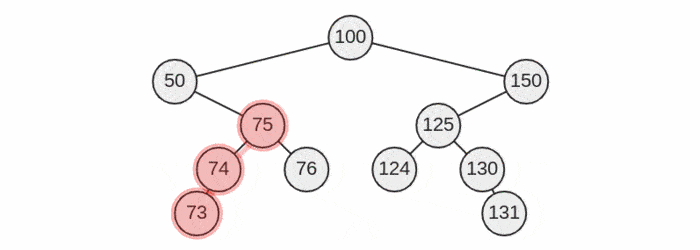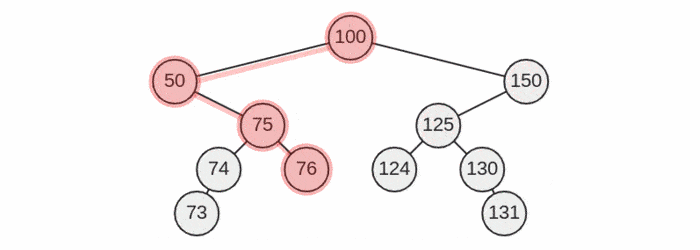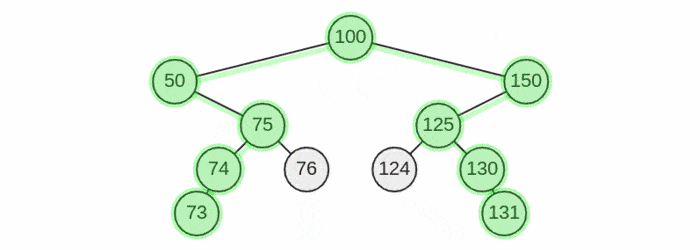
Solution Step

Depth of a node is max(depth of node.left, depth of node.right) + 1.
While we do, a path “through” this node uses 1 + (depth of node.left) + (depth of node.right) nodes.
Let’s search each node and remember the highest answer found in some path. The desired length is 1 minus this number.

Pseudo Code

// Utility function takes root and reference variable ans
int heigtht(TreeNode root, int &ans){
    if(root){
        int left = this.height(root.left, ans)
        int right = this.height(root.right, ans)
        ans = max(ans, 1 + l + r)
        return 1 + max(l, r)
    }
    return 0
}

int diameterOfBinaryTree(TreeNode root) {
    int ans = 1
    height(root, ans)
    return ans - 1
}

Complexity Analysis

Time Complexity: O(n), since we must visit each node.

Space Complexity: O(log n), if a balanced tree, O(n) otherwise. Space complexity is due to recursion.

Critical Ideas to Think

Can you write a recurrence relation for this approach?
Why did we pass the ans variable as a reference?

2. Iterative Solution

The idea is to use post-order traversal which means, make sure the node is there till the left and right child are processed. We can use the peek method in the stack to not pop it off without being done with the left and right child nodes. Then for each node calculate the max of the left and right subtrees depth and also simultaneously calculate the overall max of the left and right subtrees count.

Pseudo Code

int diameterOfBinaryTree(TreeNode root) {
    if( root is null){
        return 0
    }
    int overallNodeMax = 0
    // for post order traversal
    Stack nodeStack
    // to store the height against each node
    Map nodePathCountMap
    nodeStack.push(root)
    while(nodeStack is not empty){
        TreeNode node = nodeStack.peek()
        if(node.left is not null and not (nodePathCountMap has node.left)){
            nodeStack.push(node.left)
        }
        else 
        if(node.right is not null and not(nodePathCountMap has node.right)){
            nodeStack.push(node.right)
        }
        else
        {
            TreeNode rootNodeEndofPostOrder = nodeStack.pop()
            int leftMax = nodePathCountMap[rootNodeEndofPostOrder.left]
            int rightMax = nodePathCountMap[rootNodeEndofPostOrder.right]
            int nodeMax = 1 + max(leftMax,rightMax)
            nodePathCountMap.put(rootNodeEndofPostOrder,nodeMax)
            overallNodeMax = max(overallNodeMax,leftMax + rightMax )
        }    
    }
    return overallNodeMax
}

Complexity Analysis

Time Complexity: O(n), since we must visit each node.

Space Complexity : O(n), due to stack and map used.

Critical Ideas to Think

Which tree traversal technique does this algorithm retain?
Why did a hash map is used here?
Can you prove that the diameter of tree is the maximum value of the left height + right height + 1 for every sub-root?
Can you think of some other approach to solve this problem iteratively?