Comparison of Sorting Algorithms

In this blog, we will analyze and compare different sorting algorithms on the basis of different parameters like Time Complexity, In-place, Stability, etc.

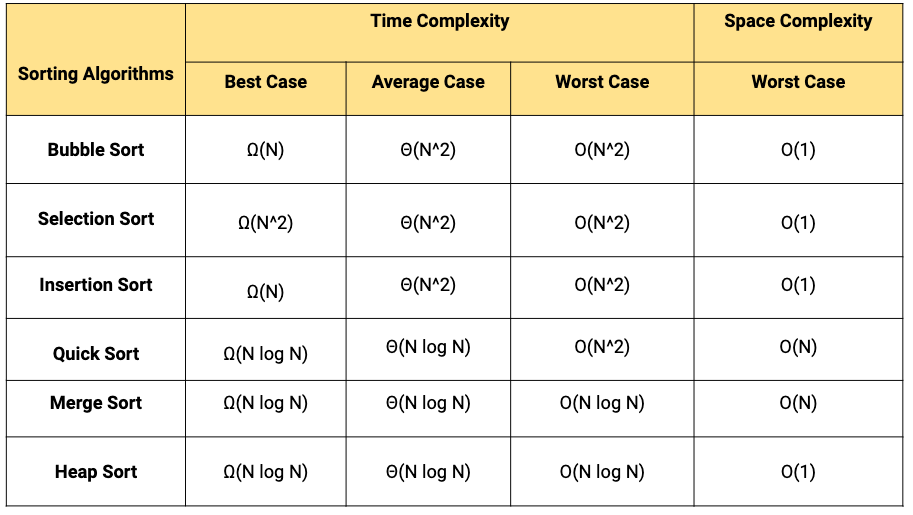
Comparison based sorting algorithms

In a comparison based sorting algorithms, we compare elements of an array with each other to determines which of two elements should occur first in the final sorted list.
All comparison-based sorting algorithms have a complexity lower bound of nlogn. (Think!)
Here is the comparison of time and space complexities of some popular comparison based sorting algorithms:

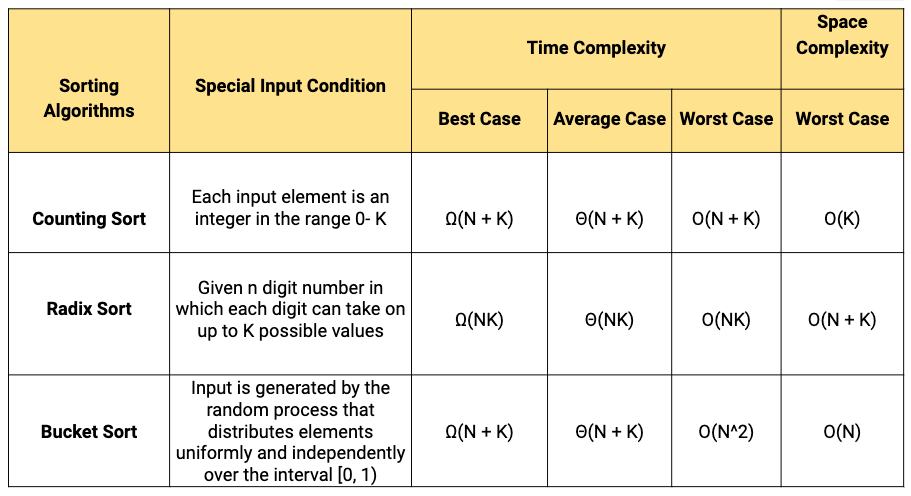
Non-comparison based sorting algorithm

There are sorting algorithms that use special information about the keys and operations other than comparison to determine the sorted order of elements.
Consequently, nlogn lower bound does not apply to these sorting algorithms.

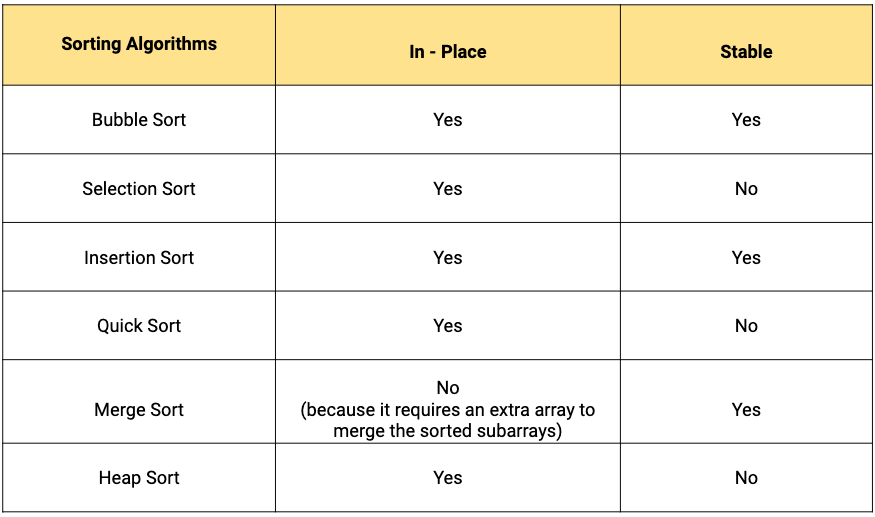
In-place and Stable sorting Algorithms

A sorting algorithm is In-place if the algorithm does not use extra space for manipulating the input but may require a small though nonconstant extra space for its operation. Or we can say, a sorting algorithm sorts in-place if only a constant number of elements of the input array are ever stored outside the array.
A sorting algorithm is stable if it does not change the order of elements with the same value.

Online/Offline: The algorithm that accepts a new element while the sorting process is going on, that algorithm is called the online sorting algorithm. From, the above sorting algorithms, the insertion sort is online.

Critical ideas to think

Understanding the sorting algorithms are the best way to learn problem solving and complexity analysis in the algorithms. In some cases, We often use sorting as a key routine to solve several coding problems.
Knowing which algorithm is best possible depends heavily on details of the application and implementation. In most practical situations, quicksort is a popular algorithm for sorting large input arrays because its expected running time is O(nlogn). It also outperforms heap sort in practice.
If stability is important and space is available, the merge sort might be the best choice for the implementation. (Think!)
Like insertion sort, quick sort has tight code and hidden constant factor in its running time is small.
When the input array is almost sorted or input size is small, then the insertion sort can be preferred.
We can prefer merge sort for sorting a linked list. (Think!)