Given the
root
node of a binary search tree (BST), write a program to find the
lowest common ancestor (LCA)
of two given nodes in the BST.
Problem Note
-
Lowest Common Ancestor:
The lowest common ancestor is defined between two nodes
node1andnode2as the lowest node in treee that has bothnode1andnode2as descendants (where we allow a node to be a descendant of itself). - All of the node values will be unique.
-
node1andnode2are different and both values will exist in the BST. - You can use extra memory, helper functions, and can modify the node struct but, you can’t add a parent pointer.
Given the following binary search tree: root = [6, 2 ,8, 1, 4, 7, 9, null, null, 3, 5]
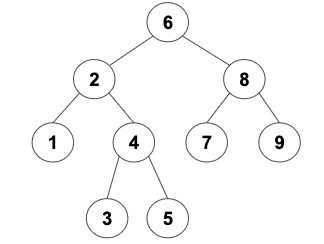
Example 1
Input: root = [6, 2, 8, 1, 4, 7, 9, null, null, 3, 5]
node1 = 2, node2 = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.Example 2
Input: root = [6, 2, 8, 1, 4, 7, 9, null, null, 3, 5]
node1 = 2, node2 = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.