Word Ladder Problem

Difficulty: Medium

Asked in: Google, Microsoft, Ebay

Problem Description

Given two words word1 and word2, and a dictionary's Dict, write a program to find the length of the shortest transformation sequence from word1 to word2, such that:

• Adjacent words in the chain only differ by one character.
• Each transformed word must exist in the dictionary. Note that word1 is not a transformed word but word2 must be in the Dict.

Problem Note:

• Return 0 if there is no such transformation sequence.
• All words have the same length.
• All words contain only lowercase alphabetic characters.
• You may assume no duplicates in the word list.
• You may assume word1 and word2 are non-empty and are not the same.

Example 1

Input: word1 = "fit", word2 = "dog", 
Dict = ["hit","hot","cot","dog","dot","log","cog"]
Output: 5
Explanation: As one shortest transformation is:
"fit"->"hit"->"hot"->"dot"->"dog"
Return its length which is 5. 
Notice "fit" is not in Dict but "dog" is.

Example 2

Input: word1 = "fool", word2 = "sage", 
Dict = ["cool","pool","poll","foil","fail","pole", "pope", "pale", "page", "sage", "sale", "fall"]

Output: 7
Explanation: As one shortest transformation is :
"fool"->"pool"->"poll"->"pole"->"pale"->"page"->"sage", Return its length which is 7.

Understanding The Problem

We are given a beginWord and an endWord. Let these two represent start node and end node of a graph. To reach startnode to the endnode we can use intermediate nodes. However, the intermediate node could only be from the given input Dict . We can move to all those nodes from the current node, if the current word is changed by a single letter.

Example 1 could be seen as →

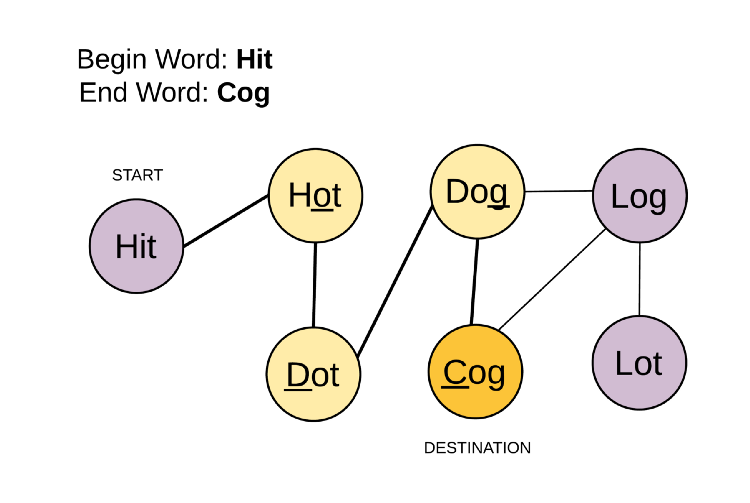
So, this clears that we have to transform the input dict into some graph where the words represent each node and the undirected edges would be according to the condition.

Solution

• Breadth-First Search: Since only one letter can be changed at a time. The idea is simply to start from the beginWord, then visit its neighbors, then the non-visited neighbors of its neighbors until we arrive at the endWord. This is a typical BFS structure.

You may try to solve this problem here.

Breadth-First Search

If we can construct a graph from the words in the given dict , then the problem could be solved using Breadth First Search .

First we have to construct the graph and for that we need to find out the neighbors of each node and to efficiently do that, we can do some pre-processing on the words of the given wordList. This pre-processing could be replacing the letter of a word by a non-alphabet say, *.

This pre-processing helps to form generic states to represent a single letter change.

For e.g. Log --> *og <-- Dog

The preprocessing step helps us find out the generic one letter away nodes for any word of the word list and hence making it easier and quicker to get the adjacent nodes. Instead, we could iterate over the entire word list and check for the words that differ by one letter and that will increase the running time complexity. This step will help build the adjacency list.

For eg. While doing BFS if we have to find the adjacent nodes for Dug we can first find all the generic states for Dug.

1. Dug => *ug
2. Dug => D*g
3. Dug => Du*

The second transformation D*g could then be mapped to Dog or Dig, since all of them share the same generic state. Having a common generic transformation means two words are connected and differ by one letter.

Now, Start from beginWord and search the endWord using BFS.

Solution Steps

1. Find all the possible generic/intermediate states using the words of Dict. Save the intermediate states in a dictionary with key as the intermediate word and value as the list of words that have the same intermediate word.
2. Push a tuple containing the beginWord and 1 in a queue. The 1 will represent the level number of a node. We have to return the level of the endNode as that would represent the shortest sequence/distance from the beginWord.
3. Use a visited dictionary to keep track of visited nodes. You may also remove the words from the input dict for every visited word.
4. Get the front element of the queue as current_word.
5. Find all the generic transformations of the current_word and find out if any of these transformations is also a transformation of other words in the word list. This is achieved by checking the dict.
6. The list of words we get from dict are all the words that have a common intermediate state with the current_word. These new set of words will be the adjacent nodes/words to current_word and hence added to the queue.
7. For each word in this list of intermediate words, append (word, level + 1) into the queue where level is the level for the current_word.
8. Eventually, you reach the desired word, its level would represent the shortest transformation sequence length.

Note: The termination condition here will be finding the endword

Pseudo Code

bool isOneDiff(string A, string B) {
    if (A.length() != B.length())
        return false
    int diff = 0
    for (int i = 0 to i < A.length()) {
        if (A[i] != B[i])
            diff = diff + 1
        if (diff > 1)
            return false
    }
    if (diff == 1) 
       return true 
    else 
       return false
}

int ladderLength(string beginWord, string endWord, set dict) {
    if (beginWord or endWord not in dict)
        return 0
    queue(string, int) que
    que.push(beginWord, 1)
    dict.erase(beginWord)
    while (not que.empty()) {
        cur = que.front()
        que.pop()
        for (auto it in dict ) {
            if (isOneDiff(cur.first, dict[it])) {
                if (dict[it] == endWord) 
                    // return the level of end word
                    return cur.second + 1
                que.push(dict[it], cur.second + 1))
                dict.erase(it)
            }
        }
    }
    return 0
}

Complexity Analysis

Time Complexity: O(M²×N), where M is the length of each word, and N is the total number of words in the input word list.

• For each word in the word list, we iterate over its length to find all the intermediate words corresponding to it. Since the length of each word is M and we have N words, the total number of iterations the algorithm takes to create all_combo_dict is M×N.
• Forming each of the intermediate words takes O(M) time because of the substring operation used to create the new string. This adds up to a complexity of O(M²×N).

Space Complexity: O(M²×N).

• For each of M intermediate words we save the original word of length M. This simply means, for every word we would need a space of M² to save all the transformations corresponding to it. Thus, all_combo_dict will need a total space of O(M²×N).
• Visited dictionary would need a space of O(M×N) as each word is of length M.
• The queue for BFS would need a space for all O(N) words and this would also result in a space complexity of O(M×N).

Combining the above steps, the overall space complexity is O(M²×N) + O(M∗N) + O(M∗N) = O(M²×N) space.

Critical Ideas to Think

• Do you think the following approach “First converting Wordlist into adjacency list Graphical representation and then using Dijkstra algorithm for finding the shortest distance between beginWord and endWord works just fine” will work for this problem? If yes, then do you think that the time complexity would be different than O(M²×N)?
• Can you perform this BFS using recursion?
• What would be the complexity of lookup in the hash?

Suggested Problems to Solve

• Minimum steps to reach the target by a Knight
• The shortest path to reach one prime to others by changing a single digit at a time
• Check if it is possible to reach a number by making jumps of two given length
• Minimum Genetic Mutation

If you have any more approaches or you find an error/bug in the above solutions, please comment down below.

Happy Coding!

Enjoy Algorithms!