What is Relational Algebra?
As we store the data at our database, how are we going to access the data? Today whatever platform we are using like Oracle9i, IBM Db2, etc. they all are using SQL(Structured Query Language). The base of this SQL is Relational Algebra. We need to understand Relational Algebra to understand the query execution and optimization in DBMS. Relational Algebra works on the entire tables in once and we don't need to use loops etc to traverse the tuples one by one. We only write a single line query and the table is traversed at once and data is fetched. So, let's dive deep into the topic and know more about Relational Algebra.
Relational Algebra
Relational Algebra is a popular procedural query language. Now, what is the meaning of procedural query language? The procedural query language is a language where to access the data from the database we have to mention ' what to do ' and ' how to do '. Now 'what to do' asks that what has to be done i.e what data we have to access the data from the database. Next point is 'how to do'. So, to access the data what are the method or procedure which we are going to use that also we have to mention. It is like C language which is a procedural language where we have to mention what the program has to do and how it has to do.
Now, there are many mathematical operations which are present in relational algebra. Some of these operations are basic and some are derived operations.
Basic Operations
- Project
- Select
- Cross Product
- Union
- Set Difference
- Rename
Derived Operations
- Join
- Intersect
Project(∏)
Project Operation is used to project or display or get the required column data from the relation. It is denoted by symbol pi(Π) . This operation eliminates duplicate values while fetching the data. Here we will be using the relational data model to understand the above operations.
Notation :
where C1, C2,...Cn are the column names of relation R.
Example: We have an employee table with attributes as Emlpoyee_id, Name, Salary, Age. We want the name and the age of the employees from the table.
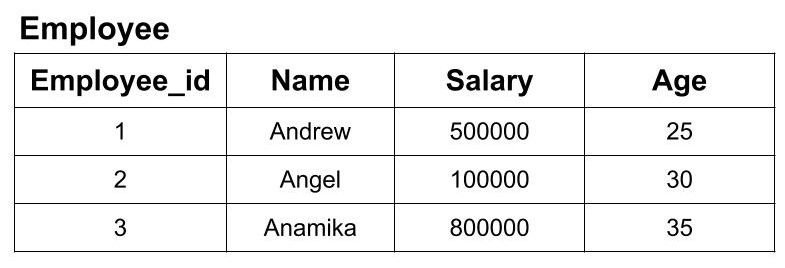
The project operation which will give us the required result is as follows:
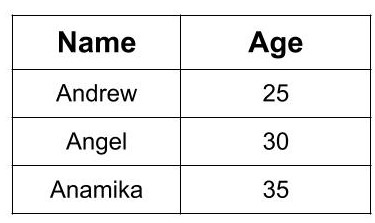
Above operation projects the Name and Age column from the Employee Table. The result of the above operation is as follows:
Select( σ)
Select operation selects the required tuples from the relation according to the given conditions. It is denoted by symbol sigma(σ) . The select operator only selects the tuples from the relation but to display those tuples we have to use the project operator.
Notation :
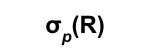
where p denotes the logic according to which the selection is done and R is the relation.
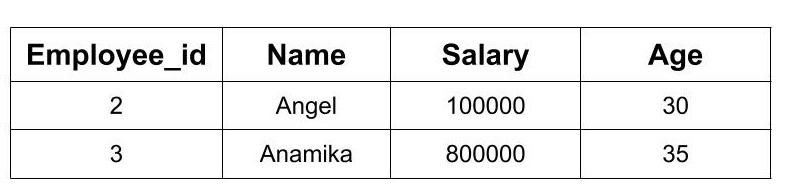
Example : We have an employee table with attributes as name, emlpoyee_id, salary, age. We want the details of all those employee whose age is greater than 26. The query for the above operation would be
The above operation would select the tuple from the employee relation. But to display the selected tuple we will have to perform the project operation. As we need all the details of the employee so we don't provide any condition in the project operation. If we don't provide any column name in project operation then it would project all the columns. So, the new query would be:
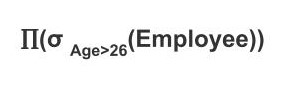
After the above operations, the result would be as follows:
Cross Product(X)
This operation is performed to merge columns from two relations. It is denoted by the symbol X . Usually, the cross operation is not meaningful but are useful when combined with some other operations like select, project etc.
Notation: R1 X R2 where R1 and R2 are two relations such that the cross product will result in a table which has all the attributes of the table R1 followed by the attributes of the R2.
Example: We have two tables of Student(S_id, Name, Class, Age) and Courses (C_id, C_name). Now, we will perform the cross product of both tables i.e
Student X Courses
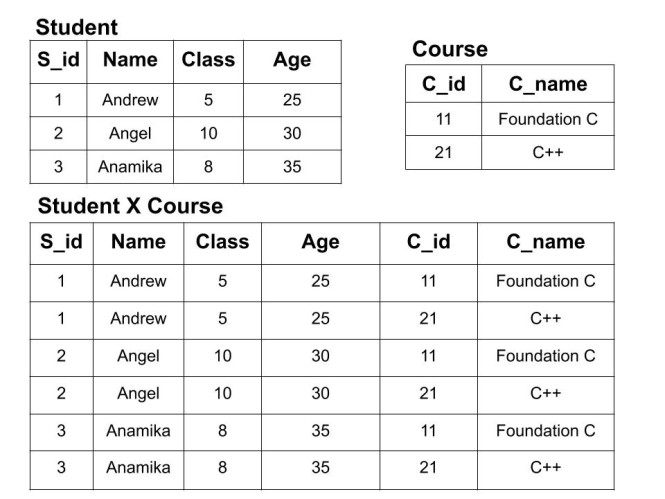
Here, every record of the student table pairs with every other record of the course table. Also, the attribute of the course table is followed by the attribute of the student table. One point to notice here is that, if the first table has m tuples and the second table has n tuples then their cross product will have m*n tuples.
Union(U)
The union operation performs the same function as the union operation in the set theory. It is represented by U symbol. If we perform an operation A U B on table A and B, then the result would include all the tuples that are in table A as well as in table B. This operation removes the duplicate tuples. For performing a union operation both the tables should have the same attributes.
Notation: R1 U R2 where R1 and R2 are two tables.
Example: We have two courses table and we want to perform the union operation on table Course_1(C_id, C_name) and Course_2(C_id, C_name). Remember, we can perform union operation only because both the tables have same attribute.
Course_1 U Course_2
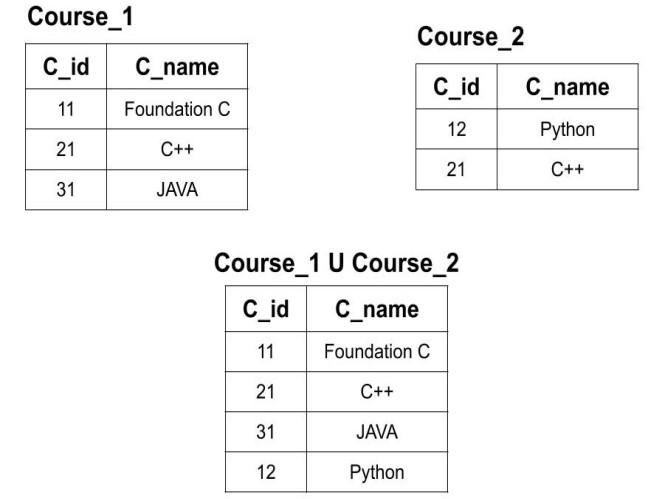
In the above example, we can see that both the tuples of the tables have been included. Also, the tuple which was common in both the tables has been removed.
Set Difference
The set difference operation performs the same function as the set difference operation in the set theory. It is represented by -(minus) symbol. If we perform an operation A-B on table A and B, then the result would include only those tuples that are in table A but not in B. This operation removes all those tuples which are common in both table A and B, from A and gives output. For performing a set difference operation both the tables should have the same attributes.
Notation: R1 - R2 where R1 and R2 are two tables.
Example: We have two courses table and we want to perform the set difference operation on table Course_1(C_id, C_name) and Course_2(C_id, C_name). Remember, we can perform set difference operation only because both the tables have same attribute.
Course_1 - Course_2
Rename
The results of the operations that we are performing are saved without any name. So, if we want to give some name to the result of any operation then we can rename the result of the operations using the rename operation. It can also be used to rename an old relation. It is denoted by symbol rho (ρ) .
Notation 1: Naming the result of an operation
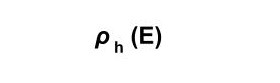
where the result of expression E is stored as h.
Notation 2: Renaming an already existing column
Exampl1e : In the above example of the 'union' operation we can to store the result of the union operation in a variable named 'All _Courses'
Example 2 : In the above example of the 'union' operation we can rename the attribute C_id of the Course_1 table to Course_id using the folllowing query.
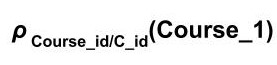
Join Operation
Join operation is used to combine two or more tables based on the related attributes. It is basically a cross product followed by some more operations like select, project etc.
There are mainly two types of join which are further divided as follows:
- Inner Join
- Natural Join
- Theta Join
- Equi Join
2. Outer Join
- Left Outer Join
- Right Inner Join
- Full Outer Join
Inner Join
Inner join is a type of join in which only those tuples are selected which full fill the required conditions. All those tuples which do not satisfy the required conditions are excluded. Let us now study in detail each type of inner join with example.
Natural Join(⋈)
Natural Join is a join which is performed if there is a common attribute between the relations.
Notation: R1 ⋈ R2 where R1 and R2 are two relations.
Example: We have two tables of Student(S_id, Name, Class, Age, C_id) and Courses(C_id, C_name). Now, we will perform natutral join on both the tables i.e
Student ⋈ Course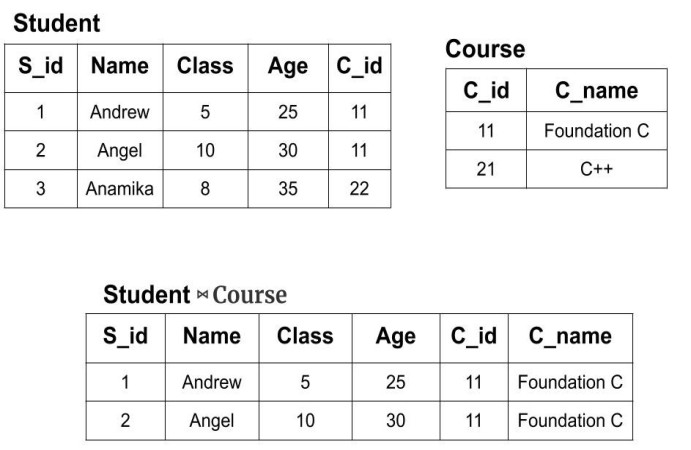
Theta Join
Theta join is a join which combines the tuples from different relations according to the given theta condition. The join condition in theta join is denoted by theta (θ) symbol. This join uses all kind of comparison operator.
Notation:
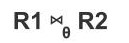
where R1 and R2 are relations such that they don't have any common attribute.
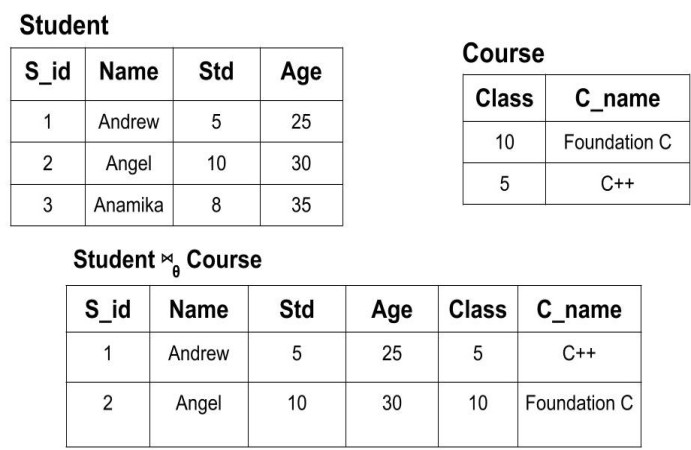
Example: We have two tables of Student(S_id,Name, Std, Age) and Courses (Class, C_name). Now, we will perform theta join on both the tables i.e
The above join operations check if the 'Std' attribute in Student is equal to the values of the 'Class' attribute of the Course table. If these values are equal then it is included in the resulting table.
Equi Join
Equi Join is a type of theta join where we use only the equality operator, unlike theta join where we can use any operator. The above example which we gave in the theta join is also an example of equi-join.
Outer Join
In Inner Join, we matched rows are returned and unmatched rows are not returned. But, in outer join, we include those tuples which meet the given condition along with that, we also add those tuples which do not meet the required condition. The result also includes the tuples from the left and right tables which do not satisfy the conditions. Based on the tuples that are added from left, right or both the tables, the outer join is further divided into three types. We will now study about its types with the help of examples.
Note: The operators here define the existence of null value which we will use to fill the table if the required conditions do not match.
Left Outer Join( ⟕)
Left Outer Join is a type of join in which all the tuples from left relation are included and only those tuples from right relation are included which have a common value in the common attribute on which the join is being performed.
Notation: R1⟕R2 where R1 and R2 are relations.
Example: We have two tables of Student(S_id, Name, Class, Age, C_type) and Courses (C_type, C_name). Now, we will perform left outer join on both the tables i.e
Student ⟕ Course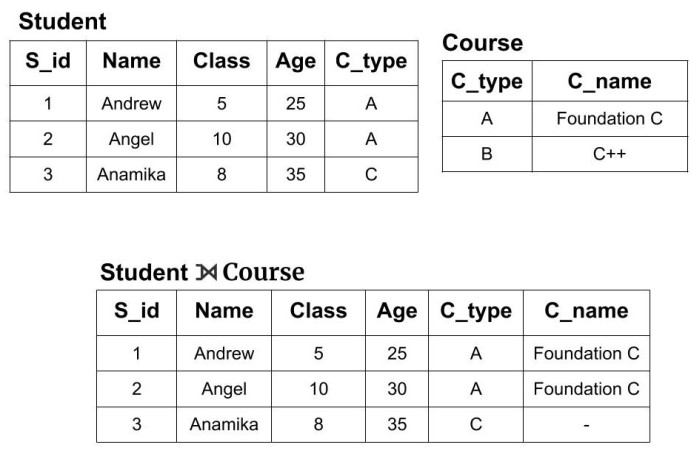 
We can see that the new resulting table has all the tuples from the Student table but it doesn't have that tuple from the course table whose attributes values was not matching. Also, it fills the table with the null value for those columns whose value is not defined.
Right Outer Join(⟖)
Right Outer Join is a type of join in which all the tuples from right relation are included and only those tuples from left relation are included which have a common value in the common attribute on which the right join is being performed.
Notation: R1 ⟖ R2 where R1 and R2 are relations.
Example: We have two tables of Student(S_id, Name, Class, Age, C_type) and Courses (C_type, C_name). Now, we will perform right outer on both the tables i.e
Student ⟖ Course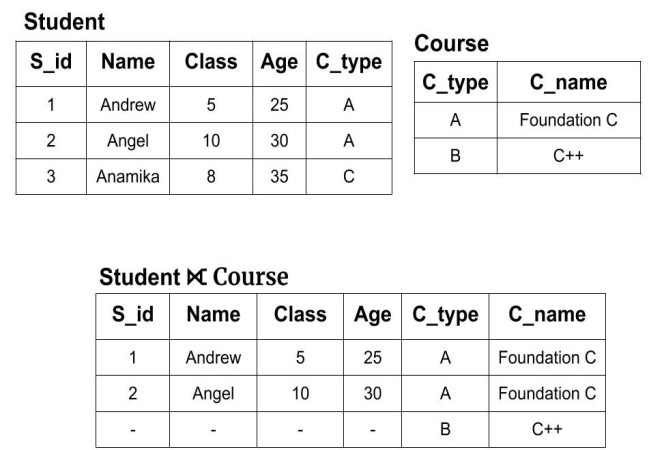
We can see that the new resulting table has all the tuples from the Course table but it doesn't have that tuple from the Student table whose attributes values was not matching. Also, it fills the table with the null value for those columns whose value is not defined.
Full Outer Join(⟗)
Full Outer Join is a type of join in which all the tuples from the left and right relation which are having the same value on the common attribute. Also, they will have all the remaining tuples which are not common on in both the relations.
Notation: R1 ⟗ R2 where R1 and R2 are relations.
Example: We have two tables of Student(S_id, Name, Class, Age, C_type) and Courses (C_type, C_name). Now, we will perform full outer join on both the tables i.e
Student ⟗ Course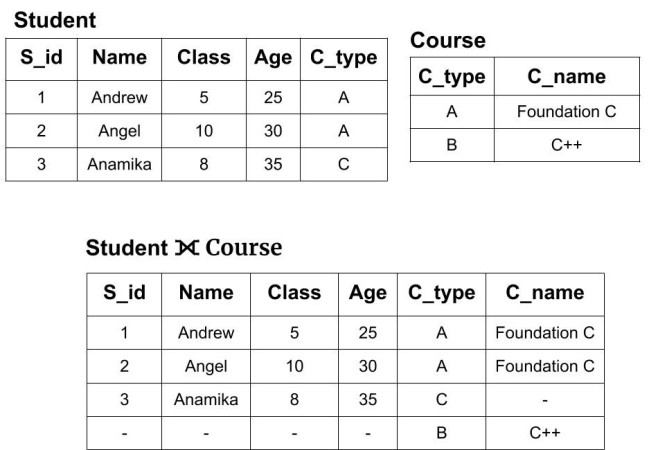
We can see that the new resulting table has all the tuples from the Course table as well as the Student table. Also, it fills the table with the null value for those columns whose value is not defined.
Intersect
The intersect operation performs the same function as the intersect operation in the set theory. It is represented by ∩ symbol. This operation selects all those tuples from the relation which are common in both the relation.
Notation: R1 ∩ R2 where R1 and R2 are two relations.
Example: We have two courses table and we want to perform the intersect operation on table Course_1(C_id, C_name) and Course_2(C_id, C_name). Remember, we can perform intesect operation only because both the tables have same attributes.
Course_1 ∩ Course_2 
So, in the above example when we perform the intersect operation we get only one tuple(21, C++) which is common in both course_1 table and course_2 table.
So, today we learnt about relational algebra and what are various operations that we can perform using relational algebra. Hope you learnt something new today.
Do share this blog with your friends to spread the knowledge. Visit our YouTube channel for more content. You can read more blogs from here .
Keep Learning :)
Team AfterAcademy!
