Time and Space Complexity Analysis of Algorithm

Every day we come across many problems and we find one or more than one solutions to that particular problem. Some solutions may be efficient as compared to others and some solutions may be less efficient. Generally, we tend to use the most efficient solution.

For example, while going from your home to your office or school or college, there can be "n" number of paths. But you choose only one path to go to your destination i.e. the shortest path.

The same idea we apply in the case of the computational problems or problem-solving via computer. We have one computational problem and we can design various solutions i.e. algorithms and we choose the most efficient algorithm out of those developed algorithms.

Critical Ideas to think!

What is a computational problem? How we extract relevant detail and transform a real-life problem into a computational problem?

What is an Algorithm?

In computer science, whenever we want to solve some computational problem then we define a set of steps that need to be followed to solve that problem. These steps are collectively known as an algorithm.

For example, you have two integers "a" and "b" and you want to find the sum of those two number. How will you solve this? One possible solution for the above problem can be:

Take two integers as input
create a variable " sum " to store the sum of two integers
put the sum of those two variables in the " sum " variable
return the " sum " variable

//taking two integers as input
int findSum(int a, int b) 
{
    int sum; // creating the sum variable
    sum = a + b; // storing the sum of a and b
    return sum; // returning the sum variable
}

In the above example, you will find three things i.e. input, algorithm, and output:

Input: Input is something for which you need to write an algorithm and transform it into the desired output. Just like in machines where you give some raw product and the machine transforms the raw product into some desirable product. In our example, the input is the two numbers i.e. "a" and "b". Before writing an algorithm, you should find the data type of input, distribution or range of input and other relevant details related to it. So critically analyse your input before writing the solution.
Algorithm: An algorithm is well-defined steps by step procedure that take some value or set of values as input and produce some value or set of values as output. In the above example, we are having three steps to find the sum of two numbers. So, all three steps are collectively called an algorithm to find the sum of two numbers.
Output: Output is the desired result in the problem. For example, if we are finding the sum of two integers a and b then for every value of a and b it must produce the correct sum as an output.

What do you mean by a good Algorithm?

There can be many algorithms for a particular problem. So, how will you classify an algorithm to be good and others to be bad? Let's understand the properties of a good algorithm:

Correctness: An algorithm is said to be correct if for every set of input it halts with the correct output. If you are not getting the correct output for any particular set of input, then your algorithm is wrong.
Finiteness: Generally, people ignore this but it is one of the important factors in algorithm evaluation. The algorithm must always terminate after a finite number of steps. For example, in the case of recursion and loop, your algorithm should terminate otherwise you will end up having a stack overflow and infinite loop scenario respectively.
Efficiency: An efficient algorithm is always used. By the term efficiency, we mean to say that:

The algorithm should efficiently use the resources available to the system.
The computational time (the time taken to generate an output corresponding to a particular input) should be as less as possible.
The memory used by the algorithm should also be as less as possible. Generally, there is a trade-off between computational time and memory. So, we need to find if the time is more important than space or vice-versa and then write the algorithm accordingly.

So, we have seen the three factors that can be used to evaluate an algorithm. Out of these three factors, the most important one is the efficiency of algorithms. So let's dive deeper into the efficiency of the algorithm.

Algorithm Efficiency

The efficiency of an algorithm is mainly defined by two factors i.e. space and time. A good algorithm is one that is taking less time and less space, but this is not possible all the time. There is a trade-off between time and space. If you want to reduce the time, then space might increase. Similarly, if you want to reduce the space, then the time may increase. So, you have to compromise with either space or time. Let's learn more about space and time complexity of algorithms.

Space Complexity

Space Complexity of an algorithm denotes the total space used or needed by the algorithm for its working, for various input sizes. For example:

vector<int> myVec(n);
for(int i = 0; i < n; i++)
    cin >> myVec[i];

In the above example, we are creating a vector of size n. So the space complexity of the above code is in the order of "n" i.e. if n will increase, the space requirement will also increase accordingly.

Even when you are creating a variable then you need some space for your algorithm to run. All the space required for the algorithm is collectively called the Space Complexity of the algorithm.

NOTE: In normal programming, you will be allowed to use 256MB of space for a particular problem. So, you can't create an array of size more 10^8 because you will be allowed to use only 256MB. Also, you can't create an array of size more than 10^6 in a function because the maximum space allotted to a function is 4MB. So, to use an array of more size, you can create a global array.

Time Complexity

The time complexity is the number of operations an algorithm performs to complete its task with respect to input size (considering that each operation takes the same amount of time). The algorithm that performs the task in the smallest number of operations is considered the most efficient one.

Input Size: Input size is defined as total number of elements present in the input. For a given problem we characterize the input size n approproately. For example:

Sorting problem: Total number of item to be sorted

Graph Problem: Total number of vertices and edges

Numerical Problem: Total number of bits needed to represent a number

The time taken by an algorithm also depends on the computing speed of the system that you are using, but we ignore those external factors and we are only concerned on the number of times a particular statement is being executed with respect to the input size. Let's say, for executing one statement, the time taken is 1sec, then what is the time taken for executing n statements, It will take n seconds.

Suppose you are having one problem and you wrote three algorithms for the same problem. Now, you need to choose one out of those three algorithms. How will you do that?

One thing that you can do is just run all the three algorithms on three different computers, provide same input and find the time taken by all the three algorithms and choose the one that is taking the least amount of time. Is it ok? No, all the systems might be using some different processors. So, the processing speed might vary. So, we can't use this approach to find the most efficient algorithm.
Another thing that you can do is run all the three algorithms on the same computer and try to find the time taken by the algorithm and choose the best. But here also, you might get wrong results because, at the time of execution of a program, there are other things that are executing along with your program, so you might get the wrong time.

NOTE: One thing that is to be noted here is that we are finding the time taken by different algorithms for the same input because if we change the input then the efficient algorithm might take more time as compared to the less efficient one because the input size is different for both algorithms.

So, we have seen that we can't judge an algorithm by calculating the time taken during its execution in a particular system. We need some standard notation to analyse the algorithm. We use Asymptotic notation to analyse any algorithm and based on that we find the most efficient algorithm. Here in Asymptotic notation, we do not consider the system configuration, rather we consider the order of growth of the input. We try to find how the time or the space taken by the algorithm will increase/decrease after increasing/decreasing the input size.

There are three asymptotic notations that are used to represent the time complexity of an algorithm. They are:

Θ Notation (theta)
Big O Notation
Ω Notation

Before learning about these three asymptotic notation, we should learn about the best, average, and the worst case of an algorithm.

Best case, Average case, and Worst case

An algorithm can have different time for different inputs. It may take 1 second for some input and 10 seconds for some other input.

For example: We have one array named " arr" and an integer " k ". we need to find if that integer " k " is present in the array " arr " or not? If the integer is there, then return 1 other return 0. Try to make an algorithm for this question.

The following information can be extracted from the above question:

Input: Here our input is an integer array of size "n" and we have one integer "k" that we need to search for in that array.
Output: If the element "k" is found in the array, then we have return 1, otherwise we have to return 0.

Now, one possible solution for the above problem can be linear search i.e. we will traverse each and every element of the array and compare that element with "k". If it is equal to "k" then return 1, otherwise, keep on comparing for more elements in the array and if you reach at the end of the array and you did not find any element, then return 0.

/*
* @type of arr: integer array
* @type of n: integer (size of integer array)
* @type of k: integer (integer to be searched)
*/
int searchK(int arr[], int n, int k) 
{  
    // for-loop to iterate with each element in the array
    for (int i = 0; i < n; ++i) 
    { 
        // check if ith element is equal to "k" or not
        if (arr[i] == k) 
            return 1; // return 1, if you find "k"
    } 
    return 0; // return 0, if you didn't find "k"
}


/*
* [Explanation]
* i = 0 ------------> will be executed once
* i < n ------------> will be executed n+1 times
* i++ --------------> will be executed n times
* if(arr[i] == k) --> will be executed n times
* return 1 ---------> will be executed once(if "k" is there in the array)
* return 0 ---------> will be executed once(if "k" is not there in the array)
*/

Each statement in code takes constant time, let's say "C", where "C" is some constant. So, whenever you declare an integer then it takes constant time when you change the value of some integer or other variables then it takes constant time, when you compare two variables then it takes constant time. So, if a statement is taking "C" amount of time and it is executed "N" times, then it will take C*N amount of time. Now, think of the following inputs to the above algorithm that we have just written:

NOTE: Here we assume that each statement is taking 1sec of time to execute.

If the input array is [1, 2, 3, 4, 5] and you want to find if "1" is present in the array or not, then the if-condition of the code will be executed 1 time and it will find that the element 1 is there in the array. So, the if-condition will take 1 second here.
If the input array is [1, 2, 3, 4, 5] and you want to find if "3" is present in the array or not, then the if-condition of the code will be executed 3 times and it will find that the element 3 is there in the array. So, the if-condition will take 3 seconds here.
If the input array is [1, 2, 3, 4, 5] and you want to find if "6" is present in the array or not, then the if-condition of the code will be executed 5 times and it will find that the element 6 is not there in the array and the algorithm will return 0 in this case. So, the if-condition will take 5 seconds here.

As you can see that for the same input array, we have different time for different values of "k". So, this can be divided into three cases:

Best case: This is the lower bound on running time of an algorithm. We must know the case that causes the minimum number of operations to be executed. In the above example, our array was [1, 2, 3, 4, 5] and we are finding if "1" is present in the array or not. So here, after only one comparison, you will get that your element is present in the array. So, this is the best case of your algorithm.
Average case: We calculate the running time for all possible inputs, sum all the calculated values and divide the sum by the total number of inputs. We must know (or predict) distribution of cases.
Worst case: This is the upper bound on running time of an algorithm. We must know the case that causes the maximum number of operations to be executed. In our example, the worst case can be if the given array is [1, 2, 3, 4, 5] and we try to find if element "6" is present in the array or not. Here, the if-condition of our loop will be executed 5 times and then the algorithm will give "0" as output.

So, we learned about the best, average, and worst case of an algorithm. Now, let's get back to the asymptotic notation where we saw that we use three asymptotic notation to represent the complexity of an algorithm i.e. Θ Notation (theta), Ω Notation, Big O Notation.

NOTE: In the asymptotic analysis, we generally deal with large input size.

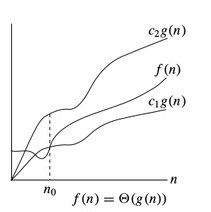
Θ Notation (theta)

The Θ Notation is used to find the average bound of an algorithm i.e. it defines an upper bound and a lower bound, and your algorithm will lie in between these levels. So, if a function is g(n), then the theta representation is shown as Θ(g(n)) and the relation is shown as:

Θ(g(n)) = { f(n): there exist positive constants c1, c2 and n0
          such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0 }

The above expression can be read as theta of g(n) is defined as set of all the functions f(n) for which there exists some positive constants c1, c2, and n0 such that c1*g(n) is less than or equal to f(n) and f(n) is less than or equal to c2*g(n) for all n that is greater than or equal to n0.

For example:

if f(n) = 2n² + 3n + 1
and g(n) = n²
then for c1 = 2, c2 = 6, and n0 = 1, we can say that f(n) = Θ(n²)

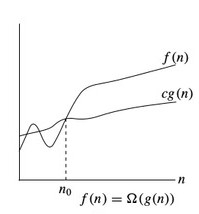
Ω Notation

The Ω notation denotes the lower bound of an algorithm i.e. the time taken by the algorithm can't be lower than this. In other words, this is the fastest time in which the algorithm will return a result. Its the time taken by the algorithm when provided with its best-case input. So, if a function is g(n), then the omega representation is shown as Ω(g(n)) and the relation is shown as:

Ω(g(n)) = { f(n): there exist positive constants c and n0 
          such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0 }

The above expression can be read as omega of g(n) is defined as set of all the functions f(n) for which there exist some constants c and n0 such that c*g(n) is less than or equal to f(n), for all n greater than or equal to n0.

if f(n) = 2n² + 3n + 1
and g(n) = n²
then for c = 2 and n0 = 1, we can say that f(n) = Ω(n²)

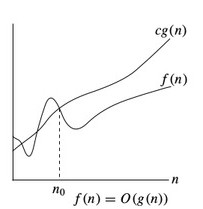
Big O Notation

The Big O notation defines the upper bound of any algorithm i.e. you algorithm can't take more time than this time. In other words, we can say that the big O notation denotes the maximum time taken by an algorithm or the worst-case time complexity of an algorithm. So, big O notation is the most used notation for the time complexity of an algorithm. So, if a function is g(n), then the big O representation of g(n) is shown as O(g(n)) and the relation is shown as:

O(g(n)) = { f(n): there exist positive constants c and n0
          such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0 }

The above expression can be read as Big O of g(n) is defined as a set of functions f(n) for which there exist some constants c and n0 such that f(n) is greater than or equal to 0 and f(n) is smaller than or equal to c*g(n) for all n greater than or equal to n0.

if f(n) = 2n² + 3n + 1
and g(n) = n²
then for c = 6 and n0 = 1, we can say that f(n) = O(n²)

Big O notation example of Algorithms

Big O notation is the most used notation to express the time complexity of an algorithm. In this section of the blog, we will find the big O notation of various algorithms.

Example 1: Finding the sum of the first n numbers.

In this example, we have to find the sum of first n numbers. For example, if n = 4, then our output should be 1 + 2 + 3 + 4 = 10. If n = 5, then the ouput should be 1 + 2 + 3 + 4 + 5 = 15. Let's try various solutions to this code and try to compare all those codes.

O(1) solution

// function taking input "n"
int findSum(int n) 
{
    return n * (n+1) / 2; // this will take some constant time c1
}

In the above code, there is only one statement and we know that a statement takes constant time for its execution. The basic idea is that if the statement is taking constant time, then it will take the same amount of time for all the input size and we denote this as O(1) .

O(n) solution

In this solution, we will run a loop from 1 to n and we will add these values to a variable named "sum".

// function taking input "n"
int findSum(int n) 
{
    int sum = 0; // -----------------> it takes some constant time "c1"
    for(int i = 1; i <= n; ++i) // --> here the comparision and increment will take place n times(c2*n) and the creation of i takes place with some constant time
        sum = sum + i; // -----------> this statement will be executed n times i.e. c3*n
    return sum; // ------------------> it takes some constant time "c4"
}
/*
* Total time taken = time taken by all the statments to execute
* here in our example we have 3 constant time taking statements i.e. "sum = 0", "i = 0", and "return sum", so we can add all the constatnts and replacce with some new constant "c"
* apart from this, we have two statements running n-times i.e. "i < n(in real n+1)" and "sum = sum  + i" i.e. c2*n + c3*n = c0*n
* Total time taken = c0*n + c
*/

The big O notation of the above code is O(c0*n) + O(c), where c and c0 are constants. So, the overall time complexity can be written as O(n) .

O(n²) solution

In this solution, we will increment the value of sum variable "i" times i.e. for i = 1, the sum variable will be incremented once i.e. sum = 1. For i = 2, the sum variable will be incremented twice. So, let's see the solution.

// function taking input "n"
int findSum(int n) 
{
    int sum = 0; // ---------------------> constant time
    for(int i = 1; i <= n; ++i) 
        for(int j = 1; j <= i; ++j)
            sum++; // -------------------> it will run [n * (n + 1) / 2]
    return sum; // ----------------------> constant time
}
/*
* Total time taken = time taken by all the statments to execute
* the statement that is being executed most of the time is "sum++" i.e. n * (n + 1) / 2
* So, total complexity will be: c1*n² + c2*n + c3 [c1 is for the constant terms of n², c2 is for the constant terms of n, and c3 is for rest of the constant time]
*/

The big O notation of the above algorithm is O(c1*n²) +O( c2*n) + O(c3). Since we take the higher order of growth in big O. So, our expression will be reduced to O(n²) .

So, until now, we saw 3 solutions for the same problem. Now, which algorithm will you prefer to use when you are finding the sum of first "n" numbers? If your answer is O(1) solution, then we have one bonus section for you at the end of this blog. We would prefer the O(1) solution because the time taken by the algorithm will be constant irrespective of the input size.

Example 2: Searching Algorithm

In this part of the blog, we will find the time complexity of various searching algorithms like the linear search and the binary search.

Linear Search

In a linear search, we will be having one array and one element is also given to us. We need to find the index of that element in the array. For example, if our array is [8, 10, 3, 2, 9] and we want to find the position of "3", then our output should be 2 (0 based indexing). Following is the code for the same:

/*
* @type of arr: integer array
* @type of n: integer(denoting size of arr)
* @type of k: integer(element to be searched)
*/
int linearSearch(int arr[], int n, int k)
{
    for(int i = 0; i < n; i++) 
        if(arr[i] == k)
            return i;
    return -1;
}
/*
* [Explanation]
* i = 0 ------------> will be executed once
* i < n ------------> will be executed n+1 times
* i++ --------------> will be executed n times
* if(arr[i] == k) --> will be executed n times
* return i ---------> will be executed once(if "k" is there in the array)
* return -1 --------> will be executed once(if "k" is not there in the array)
*/

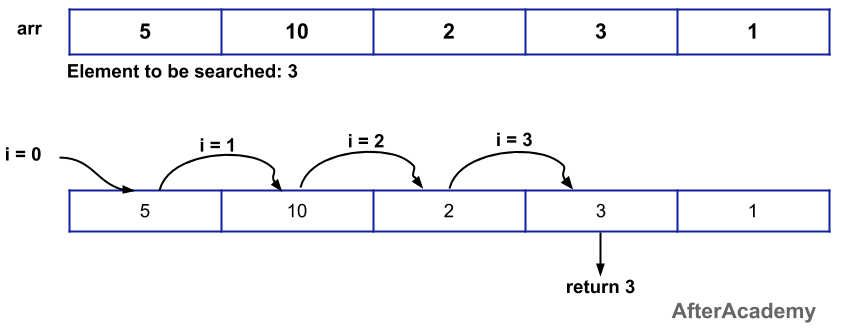
The worst-case time complexity of linear search is O(n) because in the worst case the " if(arr[i] == k) " statement will be executed "n" times.

Binary Search

In a binary search, we will be having one sorted array and an element will be given. We have to find the position of that element in the array. To do so, we follow the below steps:

Divide the whole array into two parts by finding the middle element of the array.
Find if the middle element is equal to the element "k" that you are searching for. If it is equal, then return the value.
If the middle element is not equal to element "k", then find if the element "k" is larger than or smaller than the middle element.
If the element "k" is larger than the middle element, then we will perform the binary search in the [mid+1 to n] part of the array and if the element "k" is smaller than the middle element, then we will perform the binary search in the [0 to mid-1] part of the array.
Again we will repeat from step number 2.

Let write the code for the same:

/*
* @type of arr: integer array
* @type of left: integer(left most index of arr)
* @type of right: integer(right most index of arr)
* @type of k: integer(element to be searched)
* @return type: integer(index of element k(if found), otherwise return -1)
*/
int binarySearch(int arr[], int left, int right, int k) 
{ 
    while (left <= right) { 
        // finding the middle element
        int mid = left + (right - left) / 2; 
        // Check if k is present at middle 
        if (arr[mid] == k) 
            return mid; // if k is found, then return the mid index
        // If k greater, ignore the left half of the array 
        if (arr[mid] < k) 
            left = mid + 1; // update the left, right will remain same 
        // If k is smaller, ignore the right half of the array
        else
            right = mid - 1; // update the right, left will remain same
    } 
    // if element is not found, then return -1 
    return -1; 
}

Let's understand the working of the above code with the help of one example.

Finding the Time Complexity of Binary Search

For finding the element "k", let's say after "ith" iteration, the iteration of Binary search stops i.e. the size of the array becomes 1. Also, we are reducing the size of our array by half after every iteration.
So, during 1st iteration the size of the array is "n", during 2nd iteration the size of the array is "n/2", during 3rd iteration the size of the array is "(n/2)/2 = n/2²", during 4th iteration the size of the array is "((n/2)/2)/2 = n/2³", and so on.
So, after the ith iteration, the size of the array will be n/2^i. Also, after the ith iteration, the length of the array will become 1. So, the following relation should hold true:

=> n/2^i = 1
=> n = 2^i
=> log2 (n) = log2 (2^i)    [applying log2 both sides]
=> log2 (n) = i * log2 (2)  
=> i = log2 (n)             [as logn (n) = 1]

So, the worst-case time complexity of Binary Search is log2 (n) .

Example 2: Sorting Algorithm

In this part of the blog, we will learn about the time complexity of the various sorting algorithm. Sorting algorithms are used to sort a given array in ascending or descending order. So, let's start with the Selection Sort.

Selection Sort

In selection sort, in the first pass, we find the minimum element of the array and put it in the first place. In the second pass, we find the second smallest element of the array and put it in the second place and so on.

/*
* @type of arr: integer array
* @type of n: integer(length of arr)
*/
void selectionSort(int arr[], int n)  
{  
    // move from index 0 to n-1  
    for (int i = 0; i < n-1; i++)  
    {
        // finding the minimum element  
        int minIndex = i;  
        for (int j = i+1; j < n; j++)  
            if (arr[j] < arr[minIndex])  
                minIndex = j;  
        // Swap the found minimum element with the ith element  
        swap(arr[minIndex], arr[i]);  
    }  
}

The worst-case time complexity of Selection Sort is O(n²) .

Bubble Sort

In bubble sort, we compare the adjacent elements and put the smallest element before the largest element. For example, if the two adjacent elements are [4, 1], then the final output will be [1, 4].

/*
* @type of arr: integer array
* @type of n: integer(length of arr)
*/
void bubbleSort(int arr[], int n)  
{  
    // move from index 0 to n-1
    for (int i = 0; i < n-1; i++)        
        for (int j = 0; j < n-i-1; j++)  
            if (arr[j] > arr[j+1])          // comparing adjacent elements
                swap(arr[j], arr[j+1]);   // swapping elements
}

The worst-case time complexity of Bubble Sort is O(n²) .

Insertion Sort

In Insertion sort, we start with the 1st element and check if that element is smaller than the 0th element. If it is smaller then we put that element at the desired place otherwise we check for 2nd element. If the 2nd element is smaller than 0th or 1st element, then we put the 2nd element at the desired place and so on.

/*
* @type of arr: integer array
* @type of n: integer(length of arr)
*/
void insertionSort(int arr[], int n)  
{  
    for (int i = 1; i < n; i++) 
    {  
        int key = arr[i];  // select value to be inserted
        int j = i - 1;     // position where number is to be inserted
        // check if previous no. is larger than value to be inserted
        while (j >= 0 && arr[j] > key) 
        {  
            arr[j + 1] = arr[j];  
            j = j - 1;  
        }  
        // changing the value
        arr[j + 1] = key;  
    }  
}

The worst-case time complexity of Insertion Sort is O(n²) .

Merge Sort

Merger Sort uses Divide and Conquer technique(you will learn more about divide and conquer in this Data Structure series). The following steps are involved in Merge Sort:

Divide the array into two halves by finding the middle element.
Call the Merge Sort function on the first half and the second half.
Now, merge the two halves by calling the Merge function.

Here, we will use recursion, so to learn about recursion, you can read from here ).

void merge(int* arr, int start, int mid, int end) 
{
	int temp[end - start + 1];        // creating temporary array
	int i = start, j = mid+1, k = 0;
	while(i <= mid && j <= end)       // traverse and add smaller of both elements in temp 
	{
		if(arr[i] <= arr[j]) 
		{
			temp[k] = arr[i];
			k += 1; i += 1;
		}
		else 
		{
			temp[k] = arr[j];
			k += 1; j += 1;
		}
	}
	// add the elements left in the 1st interval
	while(i <= mid) 
	{
		temp[k] = arr[i];
		k += 1; i += 1;
	}
	// add the elements left in the 2nd interval
	while(j <= end) 
	{
		temp[k] = arr[j];
		k += 1; j += 1;
	}
	// updating the original array to have the sorted elements
	for(i = start; i <= end; i += 1) 
	{
		arr[i] = temp[i - start]
	}
}


/*
* @type of arr: integer array
* @type of start: starting index of arr
* @type of end: eningd index of arr
*/
void mergeSort(int *arr, int start, int end) 
{
	if(start < end) 
	{
		int mid = (start + end) / 2; // finding middle element
		mergeSort(arr, start, mid);  // calling mergeSort for first half
		mergeSort(arr, mid+1, end);  // calling mergeSort for second half
		merge(arr, start, mid, end); // calling merge function to merge the arrays
	}
}

The worst-case time complexity of Merge Sort is O(n log(n) ) .

The following table shows the best case, average case, and worst-case time complexity of various sorting algorithms:

-----------------------------------------------------------------------------
|Sorting Algorithm |    Best Case     |   Average Case   |    Worst Case    |
|------------------|------------------|------------------|------------------|
|Selection Sort    |       Ω(n²)      |      θ(n²)       |       O(n²)      |
|Bubble Sort       |       Ω(n)       |      θ(n²)       |       O(n²)      |
|Insertion Sort    |       Ω(n)       |      θ(n²)       |       O(n²)      |
|Merge Sort        |   Ω(n logn(n))   |   θ(n logn(n))   |   O(n logn(n))   |
|Quick Sort        |   Ω(n logn(n))   |   θ(n logn(n))   |       O(n²)      |
|Heap Sort         |   Ω(n logn(n))   |   θ(n logn(n))   |   O(n logn(n))   |
|Radix Sort        |      Ω(nk)       |      θ(nk)       |       O(nk)      |
|Bucket Sort       |     Ω(n + k)     |     θ(n + k)     |       O(n²)      |
-----------------------------------------------------------------------------

Bonus Section :)

So, here is one bonus section for you. This will help you in choosing the best solution for a particular question that you will be solving on our website .

So, when you solve some coding questions, then you will be given some input constraints and based on those constraints you have to decide the time complexity of your algorithm. Generally, a typical computer system executes 10^18 operations in one second. So, if the time limit for a particular question is one second and you are trying to execute more than 10^18 instruction per second, then you will get Time Limit Exceed(TLE) error. So, based on the input size, you should decide the time complexity of your algorithm. The following table will help you to decide the time complexity of your algorithm based on the input size:

--------------------------------
|Input Size |  Max Complexity  |
|-----------|------------------|
|10^18      |       O(logn)    |
|10^8       |       O(n)       |
|10^7       |       O(nlogn)   |
|10^4       |       O(n^2)     |
|10^2       |       O(n^3)     |
|9*10       |       O(n^4)     |
--------------------------------

Use this table to decide the complexity of your code before writing the code for any problem and get rid of the TLE (thank me by solving questions from here ;))

Conclusion

In this blog, we learned about the time and space complexity of an algorithm. We saw how these two factors are used to analyse the efficiency of an algorithm. So, basically, there is a trade-off between time and space. If time is less then in most of the cases, space will be more and vice versa. That's it for this blog. Hope you learned something new today.