Search in a 2-D Matrix

Search a 2-D Matrix

Difficulty: Medium

Asked in: Amazon, Microsoft

Understanding The Problem

Problem Description

You are given a matrix arr of m x n size. Write a program to search for a value k in arr . This arr has the following properties:

Integers in each row are sorted from left to right.
The first value of each row is greater than the last value of the previous row.

If the value is found, then return 1 otherwise return 0. Example 1

Input:
arr[][] = [
          [23, 25, 35, 37],
          [40, 41, 42, 43],
          [50, 60, 74, 80]
        ]
k = 41
Output: 1
Explanation: The value 41 is present in the array arr. So, 1 is returned.

Example 2

Input:
arr[][] = [
          [23, 25, 35, 37],
          [40, 41, 42, 43],
          [50, 60, 74, 80]
        ]
k = 100
Output: 0
Explanation: The value 100 is not present in the array arr. So, 0 is returned.

Solutions

We will be discussing various solutions for the problem

Linear traversal : Traverse throughout the matrix, while comparing each element with the target
Remove row col in each comparison : Starting from the top right of matrix, move towards the bottom left in search of the target element.
Binary Search : Considering the matrix as a single array, perform a binary search for the target.

You may try this problem here.

1. Linear Search

The simple idea is to traverse the array and to compare the target element with all the elements in the matrix one by one.

Solution Step

Run a nested loop, outer loop for row and inner loop for the column
Check every element with target and if the element is found then return True
If the element is not found, then return False.

Pseudo Code

bool searchMatrix(int[][] matrix, int target) { 
    if(matrix.empty())
        return false
    int n = matrix.size()
    int m = matrix[0].size()
    
    for(int i = 0 to i < m) { 
        for(int j = 0 to j < n) 
        //if the element is found 
        if(mat[i][j] == target) { 
            return true
        } 
    } 
    return false  
}

Complexity Analysis

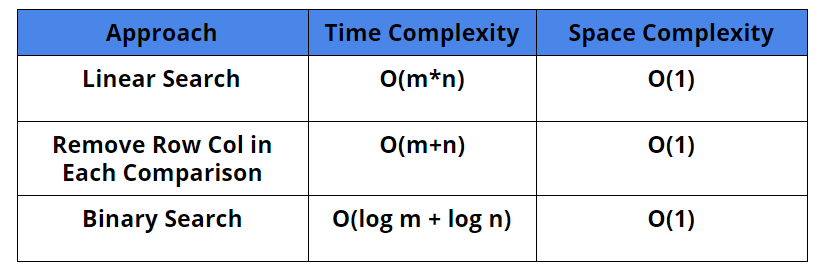
Time Complexity: O(m*n)

Space Complexity: O(1)

Critical Ideas To Think

Did we use the sorted rows characteristic of the input matrix to search the target element?
Can you think of a better approach in terms of time complexity?

2. Remove row col in each comparison

Start from the top right corner: row = 0, col = m-1

if matrix[row][col] is equal target, return true.
if matrix[row][col] is less than the target, row = row + 1; indicates that this row can’t contain the target because this one in this line is the biggest one, counting from ‘row’.
if matrix[row][col] is greater than the target, col = col — 1 ; indicate that this column can’t contain the target because this one in this column is the smallest one, counting from ‘col’.

Pseudo Code

bool searchMatrix(int[][] matrix, int target) {
    if(matrix.empty())
        return false
    int n = matrix.size()
    int m=matrix[0].size()
    int row = 0,col = m-1
    while(row < n and col >= 0){
        if(matrix[row][col] == target)
            return true
        else if(matrix[row][col] < target)
            row = row + 1
        else 
            col = col - 1
    }
    return false
}

Complexity Analysis

Time Complexity: O(m + n)

Space Complexity: O(1)

Critical Ideas To Think

Why did we increment row when matrix[row][col] < target ?
How we are reducing our problem space on each comparison?
Try this algorithm by dry running over some examples.

3. Binary Search

The problem statement states that the values of the last col of the ith row is greater than the first col of (i+1)th row. Also, each row is sorted.

This means that, if will linearly arrange the elements of each row, we will have a sorted array. So we can now perform a binary search over it.

How will the matrix behave like an array without actually creating an auxiliary array?

It could be achieved by the following formula →

A n * m matrix converted into an array: matrix[x][y] → a[x * m + y]

An array can be converted into n * m matrix: a[x] → matrix[x / m][x % m]

Solution Steps

Operate the matrix as an array using the above formula
Perform a binary search for the target element over the matrix

Pseudo Code

bool searchMatrix(int[][] matrix, int target) {
    int n = matrix.size()
    int m = matrix[0].size()
    int l = 0, r = m * n - 1
    while (l != r){
        mid = (l + r - 1) / 2
        if (matrix[mid / m][mid % m] < target)
            l = mid + 1
        else 
            r = mid
    }
    if( matrix[r / m][r % m] == target )
        return true
    else
        return false
}

Complexity Analysis

Time Complexity: O(log(m*n)) = O(log(m) + log(n))

Space Complexity: O(1)

Critical Ideas To Think

Why did we initialize r with m*n -1 ?
What will be the mid position of l and r in the matrix?
How did we convert the array index into the matrix index and matrix index into the array index?