Recursive Insertion Sort

Difficulty: Medium

Understanding The Problem

Problem Description

Write a program for the recursive implementation of Insertion Sort.

Example 1

Input: arr[] = [5, 2, 3, 1]
Output: [1, 2, 3, 5]
Explanation: The output is the sorted array.

Example 2

Input: arr[] = [5, 1, 1, 2, 0, 0]
Output: [0, 0, 1, 1, 2, 5]
Explanation: The output is the sorted array.

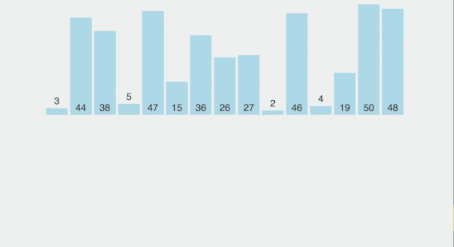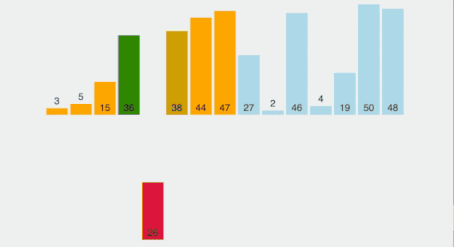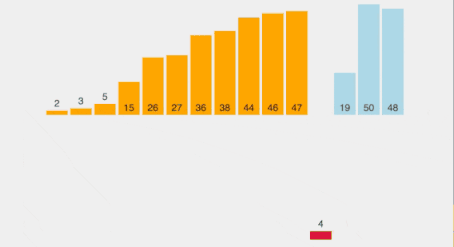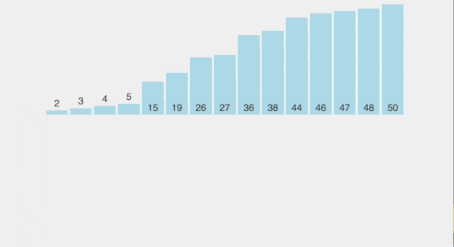
An insertion sort works like this

Solution

The problem expects us to sort an array using Insertion sort and we have to do it recursively. You can read about insertion sort here.

Now, we know that Recursion is made for solving problems that can be broken down into smaller, repetitive problems. In this case, we can define our smaller problems in this way “we have a sorted array and now we have to insert a number in that sorted array”.

Now, every recursive function requires a base case for its termination. In this case, we can say that if the array is of size 1, then the array is already sorted and we can simply return from there.

Now, the problem is to find a way to insert a value in a sorted array and that can be done as shown in the above visualization. We will simply shift the array elements to find the right position for the new element. As soon as we place the new element in its correct position, our sorted array size will increase by one.

Example:

arr = [ 5, 2, 9, 7, 14, 8], size = 6
insertion-sort(arr, 0)
    insert 5
    return arr = [5]
insertion-sort(arr, 1)
    insert 2
    return arr = [5, 2]
insertion-sort(arr, 2)
    insert 9
    return arr = [2, 5, 9]
insertion-sort(arr, 3)
    insert 7
    return arr = [2, 5, 7, 9]
insertion-sort(arr, 4)
    insert 14
    return arr = [2, 5, 7, 9, 14]
insertion-sort(arr, 5)
    insert 8
    return arr = [2, 5, 7, 8, 9, 14]

You can try this problem here.

Solution Steps

Base Case: If array size is 1 or smaller, return.
Recursively sort first n-1 elements.
Insert the last element at its correct position in the sorted array.

Pseudo Code

void recursive_insertion_sort(int arr[], int n) { 
    // Base case 
    if (n <= 1) 
        return
    // Sort first n-1 elements 
    recursive_insertion_sort( arr, n-1 )
    int val = arr[n-1]
    int pos = n-2
    while (pos >= 0 && arr[pos] > val) { 
        arr[pos+1] = arr[pos]
        pos = pos - 1
    } 
    arr[pos+1] = val
}

Complexity Analysis

Time Complexity: O(n²)

Space Complexity: O(n) (How?)

Critical Ideas To Think

Can you prove that our assumption about the array is sorted in each recursion frame is correct for every case?
Why did we initialize pos with n-2 ?
In the last line of pseudo-code, how did we make sure that pos+1 is the correct position for the val to be inserted such that the array[0..n] will stay sorted?
Can you draw the recursion tree for this sorting?
Is this solution intuitive to you?
How this approach is different from the iteration?