Rain Water Trapping

Difficulty: Hard

Asked in: Amazon, Google

Understanding the problem

Problem Description: Given n non-negative integers representing an elevation map where the width of each bar is 1.

Write a program to compute how much water it is able to trap after raining.

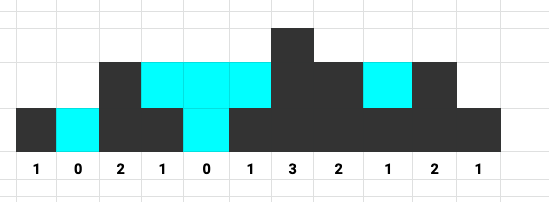
The above elevation map is represented by array [1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.

Example

Input: [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6

Before proceeding, you may try to solve this problem here.

Solutions

1. Naive Approach — Add the trapped water for each index by examining every other possible index.
2. Dynamic Programming — Use two arrays to store max heights from left and right.
3. Stack Based Approach — Use a stack to keep track of the bars that are bounded by longer bars
4. Two Pointer Approach — Take two pointers to keep track of the height of bars that could store water.

1. Naive Approach

For each element in the array, we find the maximum level of water it can trap after the rain, which is equal to the minimum of the maximum height of bars on both the sides minus its own height.

Solution steps

1. Take a variable maxWater to store maximum water and initialize it with 0
2. For every index of the array, do the following

• Find the highest bar on its left and store it in leftHeight
• Find the highest bar on its right and store it in rightHeight
• Update maxWater with maxWater + min(leftHeight, rightHeight)-arr[i]

3. Return maxWater

Pseudo Code

int maxWaterTrapped(int[] height, int size) {
    int maxWater = 0
    for (int i = 1 to size-1) {
        int leftHeight = height[i]
        for (int j = 0 to i)
            leftHeight = max(leftHeight, height[j])
        int rightHeight = height[i]
        for (int j = i+1 to size) 
            rightHeight = max(rightHeight, height[j])
        // Update the maximum water 
        maxWater = maxWater + (min(leftHeight, rightHeight) - height[i])
    }
    return maxWater
}

Complexity analysis

Time complexity: O(n²).

Space complexity: O(1).

Critical Ideas to Think

• How did we find out the amount of water trapped inside every pair of bars?
• What do leftHeight and rightHeight represent?

2. Dynamic Programming

In brute force, we iterate over the left and right parts again and again just to find the highest bar size up to that index. But, this could be stored, i.e. dynamic programming.

The concept is illustrated as shown:

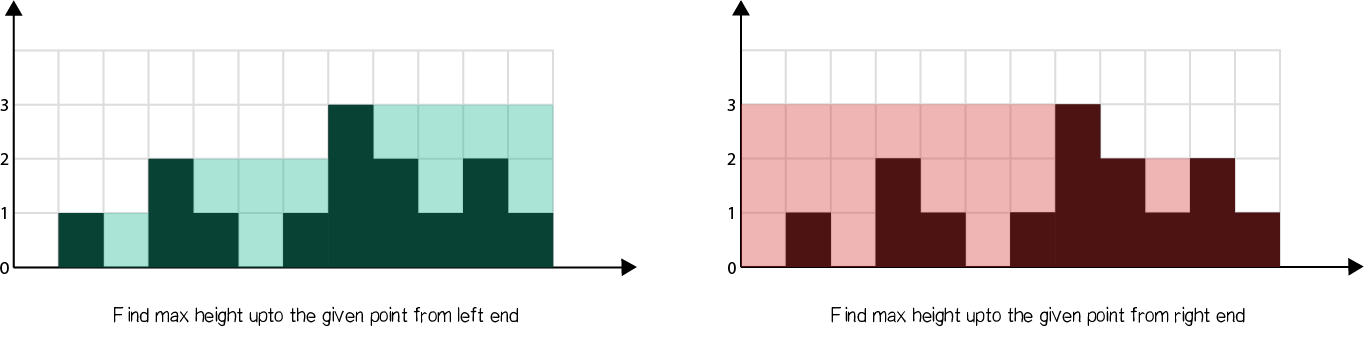
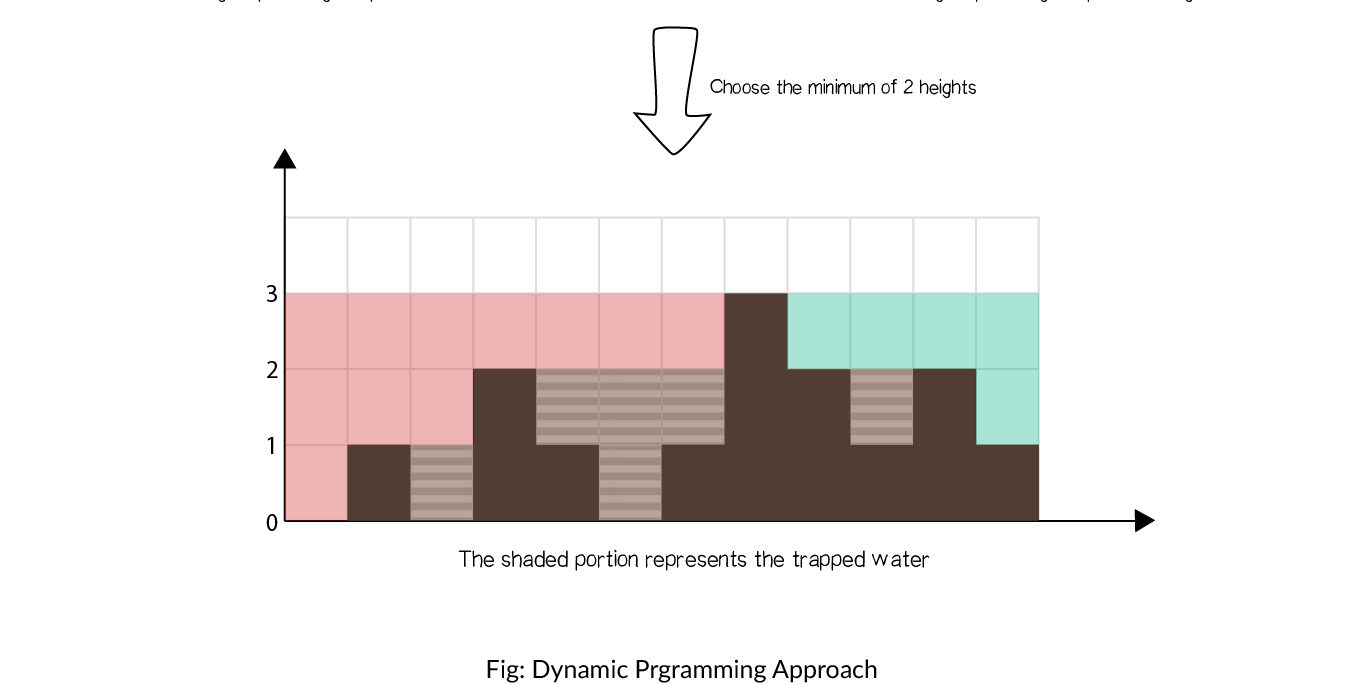
Solution steps

• Find the maximum height of the bar from the left end up to an index i in the array left_max.
• Find the maximum height of the bar from the right end up to an index i in the array right_max.
• Iterate over the height array and update maxWater as→

Add min(max_left[i], max_right[i]) − height[i] to answer

Pseudo Code

int maxWaterTrapped(int[] height, int size) {
    int maxWater = 0
    int left_max[size], right_max[size]
    left_max[0] = height[0]
    for (int i = 1 to size) {
        left_max[i] = max(height[i], left_max[i - 1])
    }
    right_max[size - 1] = height[size - 1]
    for (int i = size - 2; i >= 0; i--) {
        right_max[i] = max(height[i], right_max[i + 1])
    }
    for (int i = 1 to size-1) {
        maxWater += min(left_max[i], right_max[i]) - height[i]
    }
    return maxWater
}

Complexity analysis

Time complexity: O(n).

Space complexity: O(n).

Critical Ideas to Think

• Why do you think that storing the max bars up to each index from start and end helps?
• How did we optimize approach 1 with this approach?

3. Stack Based Approach

Instead of storing the largest bar up to an index, we can use a stack to keep track of the bars that are bounded by longer bars and hence, may store water. Using the stack, we can do the calculations in only one iteration.

We keep a stack and iterate over the array. We add the index of the bar to the stack if the bar is smaller than or equal to the bar at top of the stack, which means that the current bar is bounded by the previous bar in the stack. If we found a bar longer than that at the top, we are sure that the bar at the top of the stack is bounded by the current bar and a previous bar in the stack, hence, we can pop it and add resulting trapped water to maxWater.

Solution steps

1. Use stack to store the indices of the bars.
2. For each bar of the array do the following

• While stack is not empty and height[current]>height[st.top()]
• It means that the stack element can be popped. Pop the top element as top.
• Find the distance between the current element and the element at top of stack, which is to be filled. distance=current−st.top()−1
• Find the bounded height bounded_height=min(height[current],height[st.top()])−height[top]
• Add resulting trapped water to answer ans+=distance × bounded_height
• Push current index to top of the stack
• Move current to the next position

Pseudo Code

int maxWaterTrapped(int[] height, int size)
{
    int maxWater = 0, current = 0
    stack st
    while (current < size) {
        while (not st.empty() and height[current] > height[st.top()]) {
            int top = st.top()
            st.pop()
            if (st.empty())
                break
            int distance = current - st.top() - 1
            int bounded_height = min(height[current], height[st.top()]) - height[top]
            maxWater += distance * bounded_height
        }
        st.push(current)
        current = current + 1
    }
    return maxWater
}

Complexity analysis

Time complexity: O(n)

Space complexity: O(n)

Critical Ideas to Think

• What we stored in the stack?
• How does storing the larger bars in stack helped in solving the problem?
• Can you dry run the above algorithm for the above test case?

4. Two Pointer Approach

We have leftMax and rightMax that record the largest heights lo and hi have seen so far.

As in DP approach, instead of computing each leftMax and rightMax separately, we can actually consider one bar at each time as our min(leftMax, rightMax) since we only care about the bar with a smaller height.

We denote two pointers lo and hi starting from two ends of the array. In the loop, we update leftMax and rightMax first.

If the current leftMax is less than rightMax, we can correctly compute the water at lo, but not the water at hi.

Let’s examine the case leftMax < rightMax. We assume a leftMax in height[0, lo]. Since we do the update first, height[lo] should be less than or equal to leftMax (it means that leftMax could have been just updated by height[lo]).

Since leftMax < rightMax, the amount of water at lo can be determined at this time, no matter what the heights between [lo + 1, hi - 1] are.

Solution steps

1. Initialize lo pointer to 0 and hi pointer to size-1
2. Do the below steps untilleft<right

• update leftMax and rightMax with max(leftMax, height[lo]) and max(rightMax, height[hi])
• update water according to leftMax and rightMax

Pseudo Code

int maxWaterTrapped(int[] height, int size) {
  int lo = 0, hi = size - 1
  int leftMax = 0, rightMax = 0
  int water = 0
  while (lo < hi) {
    // update
    if (height[lo] > leftMax)  
        leftMax = height[lo]
    if (height[hi] > rightMax) 
        rightMax = height[hi]
    // compute
    if (leftMax < rightMax) { 
        // consider the min
        water += (leftMax - height[lo])
        lo = lo + 1
    } else {
        water += (rightMax - height[hi])
        hi = hi - 1
    }
  }
  return water
}

Complexity analysis

Time complexity: O(n)

Space complexity: O(1)

Critical Ideas to Think

• How are we updating these two pointers?
• Why do you feel this algorithm should work?
• Why did we update one of the two pointers only when it came across the smaller bar?

Comparison of solutions

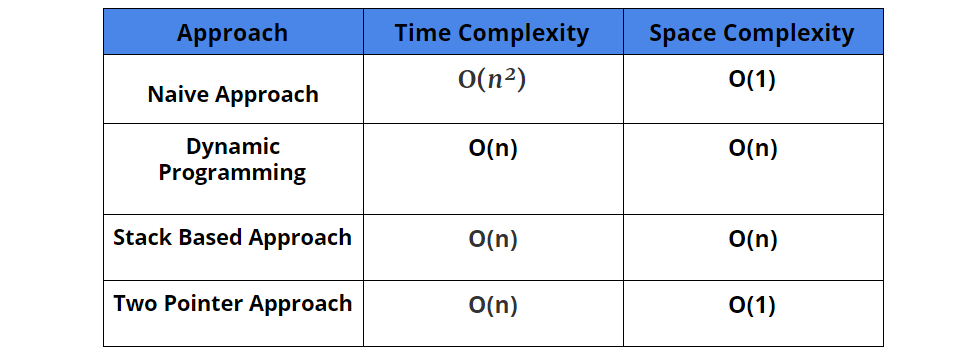
Suggested problems to Solve

• Container with most water
• Product of array except for itself
• Pour water
• Smallest subarray with an equal number of odd and even elements

If you have any more approaches or you find an error/bug in the above solutions, please comment down below.

Happy Coding! Enjoy Algorithms!