Queue and its basic operations

What is queue?

First, let us see the properties of data structures that we already do know and build-up our concepts towards the queue data structure.

Array: Its a random-access container, meaning any element of this container can be accessed instantly.
Linked List: It's a sequential-access container, meaning that elements of this data structure can only be accessed sequentially.

→ Following a similar definition, a queue is a container where only the front and back elements can be accessed or operated upon.

Queue is a data structure following the FIFO(First In, First Out) principle.

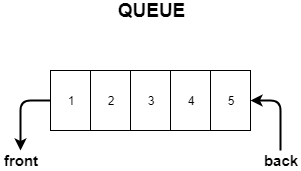
You can imagine an actual queue for a ticket counter for visual aid.

The first person in the queue is the first one to get the ticket and hence is the first to get out.

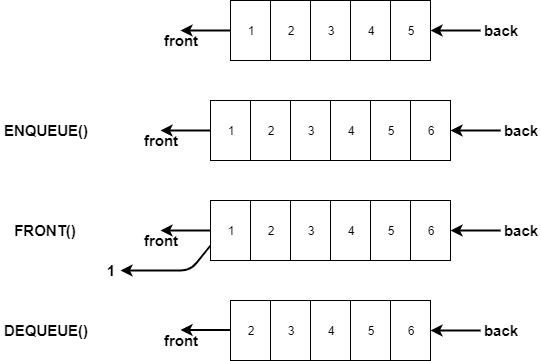
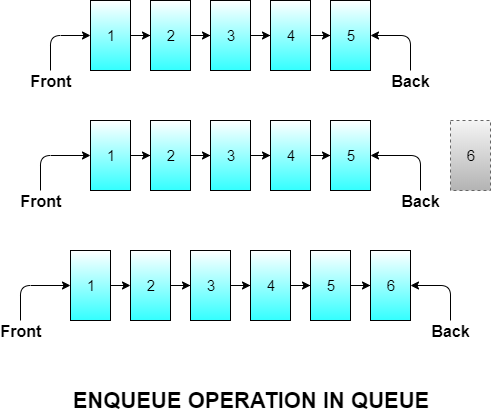
Enqueue Operation

Enqueue means inserting an element in the queue. In a normal queue at a ticket counter, where does a new person go and stand to become a part of the queue? The person goes and stands in the back . Similarly, a new element in a queue is inserted at the back of the queue.

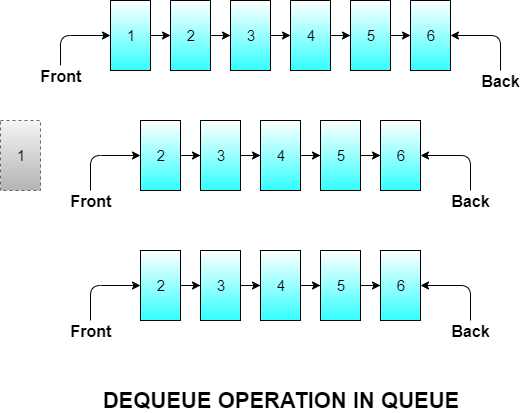
Dequeue Operation

Dequeue means removing an element from the queue. Since queue follows the FIFO principle we need to remove the element of the queue which was inserted at first. Naturally, the element inserted first will be at the front of the queue so we will remove the front element and let the element behind it be the new front element.

Front Operation

This is similar to the peek operation in stacks, it returns the value of the element at the front without removing it.

isEmpty: Check if the queue is empty

To prevent performing operations on an empty queue, the programmer is required to internally maintain the size of the queue which will be updated during enqueue and deque operations accordingly. isEmpty() conventionally returns a boolean value: True if size is 0, else False.

Queue Implementation

The key idea of queue implementation is to use both ends of the queue: front end for deleting elements and back/rear end for inserting elements. This is as simple as its concept because we just need to simply keep in mind all of its properties and operations.

You should remember one very important thing though →

All operations in the queue must be of O(1) time complexity.

We shall be implementing queue in two different ways by changing the underlying container: Array and Linked List.

1. Array Implementation of Queue

An array is one of the simplest containers offering random access to users based on indexes. But what are the access criteria in a queue? Can you access any element of the queue? No. Only the first and last elements are accessible in a queue.

So first, after initializing an array, we need two pointers, one each to point to the front end and back end. Instead of using actual pointers, we will use indexes, front and back will hold index positions of front end and back end respectively.

int queue[8]
int front = -1
int back = -1

Here, 8 is a pre-defined capacity of the queue. The size of a queue should not exceed this limit

★ The default value for front and back is -1, denoting that the queue is empty. Let us wrap this group of data members in a class:

class Queue
{
    int arr[]
    int capacity
    int front
    int back
}

Let us also create a constructor which initializes capacity, front and back.

Queue(int cap)
{
    capacity = cap
    front = -1
    back = -1
}

★ You are also required to allocate memory to arr according to the conventions of the language you use to implement it.

In order to improve our memory utilization, we will implement what's known as a circular queue. To implement a circular queue, we would need a circular array. Don't stress, its quite similar to our normal array. So much that its declaration is not even slightly different.

In a circular array, the index after the last element is that of the first element.

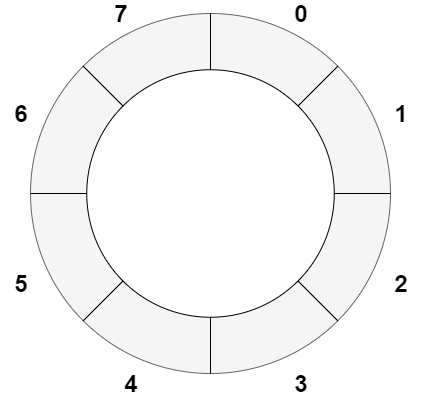
So how would we traverse in such an array? Should we keep an if statement to check if the index is less than 8 or not? Alternatively, we could always use the remainder after dividing by 8 when increasing index.

arr[(i+1) % capacity]

That is primarily the only difference. Whenever we increase index in a circular array, we take modulo with the size of the array to proceed to the next element.

Now, we need to implement the operations that we generally perform in a queue.

Enqueue Operation

Where do we insert an element in a queue? In the back.

And how do we do it?

The value of back is increased by 1
A new element is inserted at the back
Be sure to increase the value of back according to the norms of circular array, i.e. (back+1) % capacity
Initially front = -1. But when we are inserting the first element in the queue then we need to update the value of front i.e. front = back. (Think!)

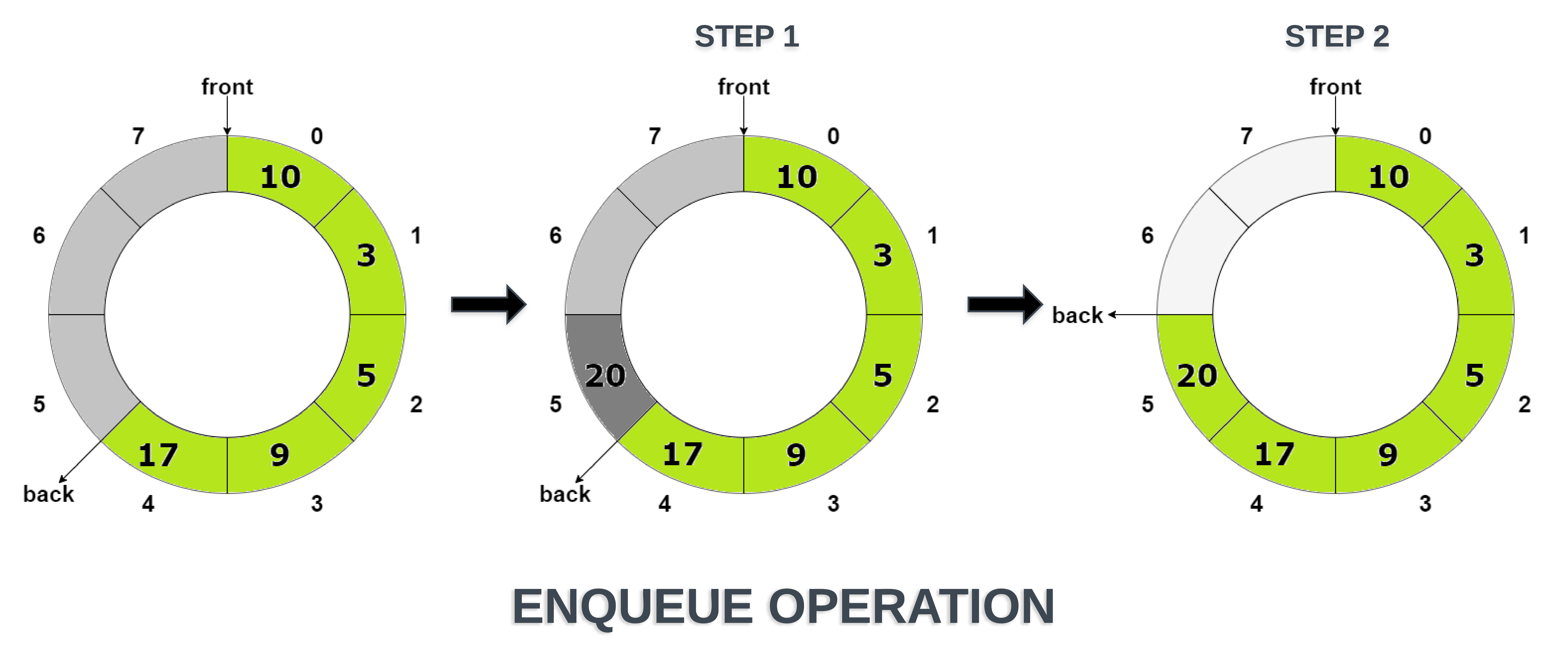
Simple, right? Any exceptions that come to mind?

▹ What if the queue is filled up to its capacity? We shall check if the queue if full before inserting a new element and throw an error if it is. How do we check if the queue is full? ( Think! )

Now, let us implement this simply

void enqueue(int item)
{
    if ((back + 1) % capacity == front)
        print("Queue if full!")
    else
    {
        back = (back+1) % capacity
        arr[back] = item
        if(front == -1)
           front = back   
    }
}

Dequeue Operation

Now that we have discussed the insertion of an element, let’s discuss the deletion of an element. Which end of the queue do we use to delete an element? The front end! How do we delete an element?

Access the element which is stored in front position i.e. item = arr[front]
if (front == back) , then this is a case of a single element in the queue. After the deletion of this single element, queue become empty. So we need to set the empty queue condition before returning the value i.e. front = back = -1 (Think!)
Otherwise, increase the value of front by 1 i.e. front = (front + 1) % capacity.
In the end, return the value stored at the item.

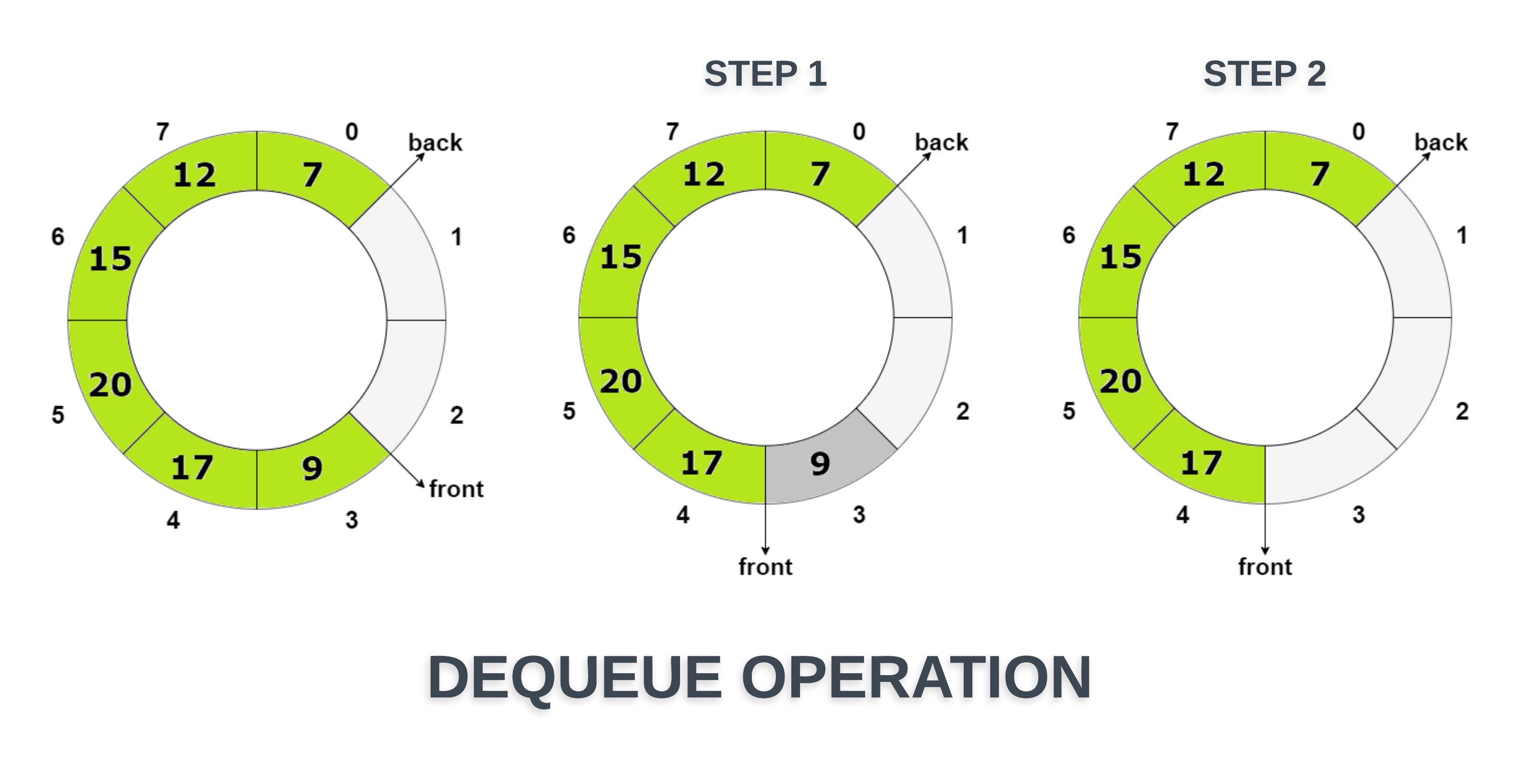
▹ Can you think of an exception in this case like the one above of the queue is full? Ans: The queue can be empty when the dequeue operation is called. We need to check for this beforehand.

Let’s try implementing it now

int dequeue()
{
    if(isEmpty() == True)
    {
        print("Queue is empty!")
        return 0
    }    
    else
    {
        int item = arr[front]
        if(front == back)
           front = back = -1
        else 
           front = (front + 1) % capacity
        return item 
    }    
}

★ But we just implemented Step 1, right? Where's Step 2?

→ Well, Step 2 is mainly deallocating any memory assigned to the element being dequeued. We were dealing with only primitive data type integer and therefore didn't need to deallocate anything.

Peek and isEmpty Operation

peek() and isEmpty() is quite simple to implement. We need to steer clear of exceptions though.

int peek()
{
    if (isEmpty() == True)
    {
        print("Queue is empty!")
        return -1
    }
    else 
        return arr[front]
}

bool isEmpty()
{
    if (front == -1)
        return True
    else
        return False
}

2. Linked List Implementation

Another way to implement a queue is to use a linked list as an underlying container. Let’s move towards the implementation part then

→ Let us assume that we have used class for linked list

class ListNode
{
    int val
    ListNode next
}

We also need two pointers that point to its front node and tail node.

What should an empty queue look like if implemented with a linked list? Ans: Its front and the back pointer will point to NULL

ListNode front = NULL
ListNode back = NULL

Is there any benefit to implementing the queue with a linked list compared to arrays? Ans: We do not need to mention the size of the queue beforehand.

→ Although, if you want to implement a limit to prevent excess use, you may need to encapsulate the class ListNode inside some other class along with a data member capacity .

class Queue
{
    int capacity
    class ListNode
    {
        int val
        ListNode next
    }
    ListNode front
    ListNode back
}

We shall be using just using class ListNode below for simplicity.Let us move towards queue operations

Enqueue Operation

The same properties hold as mentioned above with an added benefit that we need not worry about the queue being full, but we do need to check if its the first element is inserted in the queue, because the values of front and back in that case would be NULL .

void enqueue(int item)
{
    ListNode temp = ListNode(item)
    
    if( isEmpty() == True )
    {
        front = temp
        back = temp
    }
   else 
    {
        back.next = temp
        back = back.next
    }
}

Dequeue Operation

Properties of linked list relaxed us from checking if the queue is full in enqueue operation. Do they provide any relaxation for exceptions in dequeue operation? No. We still need to check if the queue is empty.

Since the front element is represented by a front pointer in this implementation. How do we delete the first element in a linked list? Simple, we make a front point to the second element

int dequeue()
{
    if ( isEmpty() == True )
    {   
        print ("Queue is empty!")
        return 0 
    }     
    else
    { 
        ListNode temp = front 
        int item = front.val
        front = front.next
        free(temp)
        return item 
    }
}

Peek and isEmpty Operation

The implementation of these two operations is pretty simple and straight-forward in linked list too.

int peek()
{
    if (isEmpty() == True)
    {
        print ("Queue is empty!")
        return -1
    }
    else
        return front.val
}

bool isEmpty()
{
    if (front == NULL)
        return True
    else
        return False
}

Augmentations in Queue

You can augment the queue data structure according to your needs. You can implement some extra operations like:-

isFull(): tells you if the queue is filled to its capacity
The dequeue operation could return the element being deleted

Application of Queues

What is the normal real-life application of queues? People wait in queues to await their chance to receive a service. Programming follows a similar concept.Let us look at some application of queue data structure in real-life applications :-

Handling of high-priority processes in an operating system is handled using queues. First come first served process is used.
When you send requests to your printer to print pages, the requests are handled by using a queue.
When you send messages on social media, they are sent to a queue to the server.
An important way of traversal in a graph: Breadth First Search uses queue to store the nodes that need to be processed.
Queues are used in handling asynchronous communication between two different applications or two different processes.