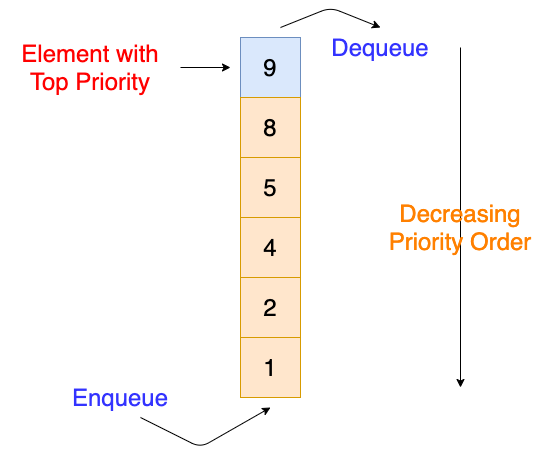
Priority Queues

Priority Queues are similar to queues where we insert an element from the back and remove an element from the front, but with one difference that the logical order of elements in the priority queue depends on the priority of the elements. In this blog, we will discuss the priority queues, its properties, its various implementations, and its applications. We will also analyze and compare the various implementations of the Priority Queue. So let’s get started with the properties of Priority Queue.

Properties

Priority Queues are the extension of the queues with the following properties:

• Each element inserted in the Priority Queue has some priority.
• The element which has higher priority is dequeued first than the element having the low priority.
• If the two elements having the same priority, then the element which entered the priority queue first will get dequeued first.

Functionality

Priority Queue supports the following functionality

• Enqueue() - Inserting the new element in the Priority Queue.
• Dequeue() - Deleting the maximum priority element from the Priority Queue.
• top() - Returning the maximum priority element in the Priority Queue.

Implementation

We can think of various ways of implementing the priority queues. We can choose various data structures like an array, linked list, BST, heaps to make the operations of the priority queues efficient.

The structure of the element of the priority queue will be

class Node {
    int data
    int priority
}

Implementation through Array

We will take an array that will store the elements of the priority queue. So, the enqueue operation will take place at the end of the array which is a constant time operation.

But, for the dequeue operation, we have to find the highest priority element in the array and delete it from the array. The deletion and the search operation in the array take linear time. Similarly, the top() will also take linear time to search for the highest priority element.

So, with an array

• enqueue() takes constant time.
• dequeue() takes linear time.
• top() takes linear time.

Now, if we maintain the order of the array with respect to priority, the enqueue() will take the linear time and dequeue() and top() will take the constant time.

Implementation through Linked List

The linked list can be created in such a way that the highest priority element should be at the front. The linked list can be arranged in the order of descending priority. So that the dequeue() operation can take constant time.

For enqueue() operation, we need to traverse the linked list and find the proper position to insert the node such that the overall order of priority queue is maintained. This will take linear time but the other two operations i.e. the dequeue() and top() can be done in constant time.

Implementation through BST

We can also implement the functionality of the priority queue using a Binary Search Tree. A typical BST takes O(logn) for both insertion and deletion operation. We can also use the self-balancing BST like AVL Tree, Red-Black Tree, etc to support the o(logn) complexity even in worst-case.

The time to find the top priority element can be done in constant time. We can keep an extra pointer to store the highest priority element and that can be updated when the insertion and deletion is performed. With deletion operation, we will update the extra pointer by finding the inorder successor.

Implementation through Heaps

Heaps are generally preferred for the implementation of a priority queue. In the heaps, the enqueue() and dequeue() can be performed in O(log n) time.

The top priority element will be present at the root Node. The heap can be built on the property that top priority element will be at the root Node so that the top priority element can be found in constant time.

The BST and heaps take the same time complexity to perform the operations of priority queue but heaps are prefered when priority queue is implemented. This is because of the following reasons:

• Heaps are implemented using arrays, so it does not require any extra space for the pointers. The parent-child relation is maintained in heaps by indexes.
• The heaps can be build in O(N) time, but Self Balancing BST requires O(nLogn) time to construct.
• The operations are of same time complexity but the constants in Binary Search Tree are higher.
• There are variations of Binary Heap like Fibonacci Heap that can support insert and decrease-key in Θ(1) time.

Enqueue Operation

Inserting an element in the priority queue(max heap) is done as

• Insert the new element at the end of the tree.

• Heapify the tree i.e. converting the new tree into a heap.

Dequeue Operation

Deleting the maximum priority element is done as

• Swap it with the last element.

• Delete the last element.

• Heapify Again i.e. converting the new tree into a heap.

Top Operation

The maximum priority element will be present as rootNode. So return the rootNode.

Pseudo Code

// arr will store the element's of the priority queue
void heapify(int arr[], int size, int i)
{
    largest = i
    leftChild = 2*i + 1
    rightChild = 2*i + 1
    
    if( leftChild < size and arr[i] < arr[leftChild])
        largest = leftChild
    
    if( rightChild < size and arr[largest] < arr[rightChild])
        largest = rightChild
    
    if( largest != i)
    {
        swap(arr[i],arr[largest])
        heapify(arr,n,largest)
    }
}

// This will return the size of the priority queue
int enqueue(int arr[], int size, int num) {
    if(size == 0) {
        arr.append(num)
    } 
    else {
        arr.append(num);
        for ( i = size/2-1 to 0 )
            heapify(arr,size,i)
    }
    return size + 1
}

// This will return the size of the priority queue
int dequeue(int arr[], int size)
{
    swap(arr[0],arr[size-1])
    size = size -  1 // decreasing the size
    for( i = size/2 -1 to 0 )
        heapify(arr,size,i)
}

// return top priority element
int top(){
    return arr[0]   
}

Applications of Priority Queue

• CPU Scheduling
• Event-driven Simulation.
• A* search algorithm in AI.
• Data compression using Huffman coding.
• Statistics (maintain the largest M values in a sequence).

Suggested Problems to Solve in Heaps

• K Pairs with Smallest Sums
• Sliding window maximum
• Merge K sorted list
• Convert a min heap to max heap

Happy coding! Enjoy Algorithms.