Minimum Spanning Tree

In the previous blogs, we learned about the Graph and its types . Now, in this blog, we will learn the concept of Minimum Spanning Tree which is asked in interviews of various companies. But before getting started with the Minimum Spanning Tree a.k.a. MST, let's get started with the concept of Spanning Tree.

What is a Spanning Tree?

We all know that a graph is represented as G = (V, E) , where G is the name of the graph which contains a set of vertices V and a set of edges E .

So, a Spanning Tree is a subset of an undirected and connected graph in which all the nodes of the graph are connected with each other with the help of (n-1) edges where n is the number of nodes or vertices present in the graph G . So, a Spanning Tree can be defined as:

If G = (V, E), here, G is the graph
Then, S ⊆ G and S = (V', E'), here, S is the Spanning Tree
Where V' = V and |E'| = |V| - 1, here |E'| = number of edges in S and |V| = number of vertices or nodes in G

The following is an example of Spanning Tree:

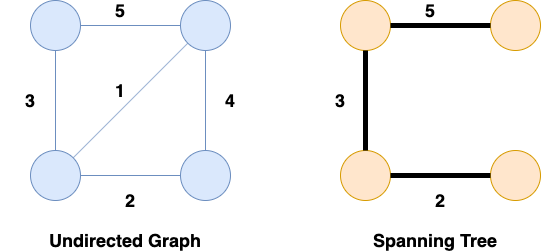
Now, you can try to draw as many Spanning Tree as possible. While drawing the Spanning Trees, one thing that can be noted here is that, if we have e edges, then we are making spanning trees of having n-1 edges, where n is the number of vertices or nodes. So, the total number of possible spanning trees are:

eC(n-1); here, e is the number of edges present in the graph and n is the total number of nodes or vertices present in the graph.

But if the graph is having some cycle not containing n vertices, then the total number of possible spanning trees are:

eC(n-1) - number of cycles present; here, e is the number of edges present in the graph and n is the total number of nodes or vertices present in the graph.

So, you can use the above formula to verify the number of Spanning Trees that you made a moment earlier. Now, let's dive deeper into the concepts of Minimum Spanning Tree.

What is a Minimum Spanning Tree?

When you are having a weighted graph i.e. the graph in which there is some weight or cost associated with every edge, then a Minimum Spanning Tree is that Spanning Tree whose cost is the least among all the possible Spanning Trees. The cost of a Spanning Tree is the sum of the weight of all the edges that are present in that Spanning Tree .

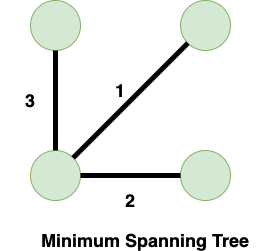
In order to find a Minimum Spanning Tree, you can construct all the possible Spanning Tree and the tree having the least cost will be your Minimum Spanning Tree. But this is a very lengthy process because here you have to find all the possible Spanning Tree. So, we need to apply some Greedy technique to find the MST and in order to do so, there are two algorithms or techniques that are used:

Kruskal's Algorithm
Prim's Algorithm

Let's learn one by one.

Kruskal's Algorithm

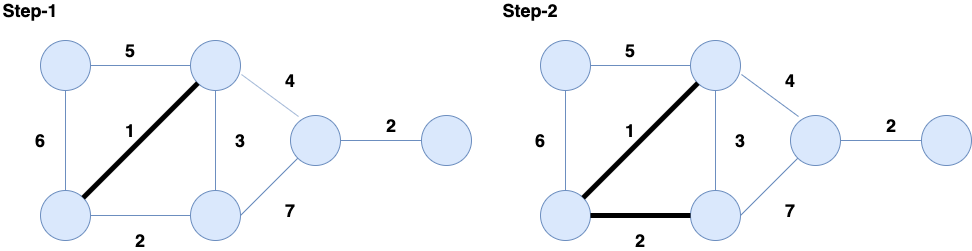
Kruskal's Algorithm is a greedy approach to find the cost of the Minimum Spanning Tree. Here, we make a list of edges that are sorted on the basis of their cost and after that, we take the smallest edge one by one. The following steps are involved in Kruskal's Algorithm:

Sort the edges of the graph based on their cost.
Add the edge having the least cost until all vertices are connected.
Add only those edges which are not forming any cycles.

The following is an example of the step by step implementation of the Kruskal's Algorithm applied to the following graph:

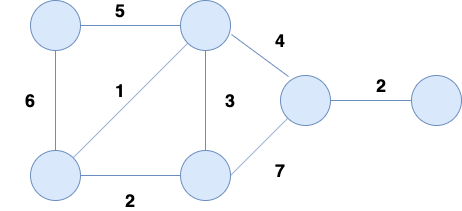
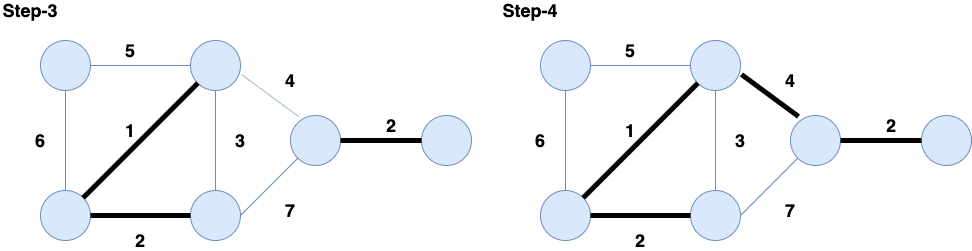
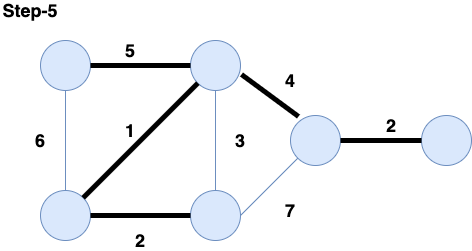
Pseudo-Code

class Edge {
    int v1
    int v2,
    int weight
}

int krushkal(int N, int E, Edge Graph[E])
{
    // sort the graph array w.r.t to weight
    sort(Graph);
    
    T = [] // contains MST 
    i = 0
    cost = 0
    // since n-1 edges can only be in spanning Tree
    while( T.length < n-1 )
    {
        if (adding Graph[i] does not make any cycle) {
            T.append(Graph[i])
            i += 1
            cost += Graph[i].weight;
        }
    }
    return cost;
}

Note:- You can use Union Find Algorithm to detect the cycle. (Try implementing that.)

Pseudo-Code Using Union Find Algorithm

id = [] // to store the parent

void union(int x, int y)
{
    p = root(x)
    q = root(y)
    id[p] = id[q]
}
int find(int x)
{
    while(id[x] != x)
    {
        id[x] = id[id[x]]
        x = id[x]
    }
    return x
}

int krushkal(int N, int E, Edge Graph[E])
{
    // sort the graph array w.r.t to weight
    sort(Graph);
    
    // Initially all vertex will be parent to itself
    for(i = 0 to N-1) 
        id[i] = i
    
    T = [] // contains MST 
    i = 0
    cost = 0
    // since n-1 edges can only be in spanning Tree
    while( T.length < n-1 )
    {
        if (find(Graph[i].v1) != find(Graph[i].v2)) {
            T.append(Graph[i])
            i += 1
            cost += Graph[i].weight;
            union(Graph[i].v1, Graph[i].v2)
        }
    }
    return cost;
}

The time complexity of Kruskal's Algorithm is O(E log V) .

Prim's Algorithm

In this type of Greedy approach, we first select the shortest edge from the given graph and after that, we will select that shortest edge which is connected to the already present nodes of the Spanning Tree that you are making. The following are the steps of Prim's Algorithm:

Maintain two disjoint sets i.e. one for those edges that are present in the Spanning Tree and other set contains the edges that are not present in the Spanning Tree.
Select the edge that is not present in the set of edges that are already present in the Spanning Tree. Also, the selected edge should be connected to any of the nodes or vertices that are present in the Spanning Tree.
While adding edges to the Spanning Tree, always verify for cycles present in the Spanning Tree i.e. if the addition of some edge results in a cycle in the Spanning Tree, then ignore adding that edge in the Spanning Tree.

The following is an example of the step by step implementation of the Prim's Algorithm on the following graph:

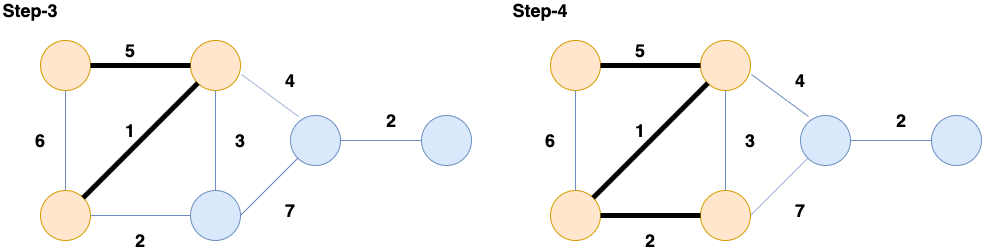
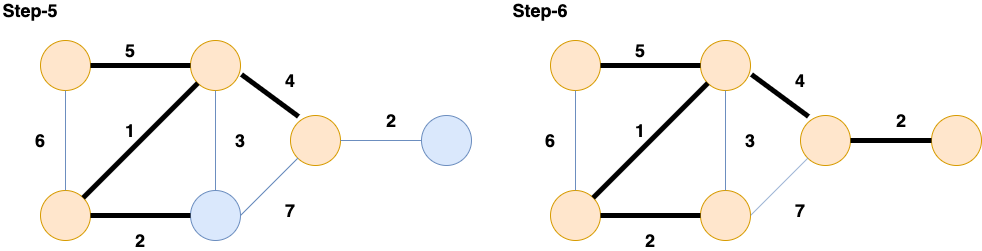
Pseudo-Code

class Edge {
    int v1
    int v2,
    int weight
}

int prim(int N, int E, Edge Graph[E])
{
    // we will maintain two sets using a boolean array
    vis = []
    // Initailly all the vertex is not added to MST
    for(i = 0 to N-1)
        vis[i] = false
        
    cost = 0

// T will store the edges of MST
    T = []
    
    cost += small.weight

// since MST will contain n-1 edges
    while(T.length < n-1)
    {
        // It will find the smallest weighted edges
        // whose atleast one vertex is not visited
        // that means it will not form cycle
        Edge small = findSmallest(Graph)
        cost += small[weight];
        vis[small.v1] = vis[small.v2] = true
        T.append(small)
    }
    
    return cost
}

Note:- Implement findSmallest() function with logrithimic time complexity. (Hint- Priority Queue)

The time complexity of Prim's algorithm is O((V + E) log V) .