Merge Overlapping Intervals

Merge overlapping intervals

Difficulty: Medium

Asked in: Amazon, Google

Understanding the Problem

You will be given a set of intervals in the form of a 2-D array, write a program to merge all the overlapping intervals and return the array.

Problem Note:

You will be given a 2-dimensional array consisting of n rows and 2 columns.
Each row has an interval starting from the value at the first column and ending at a value in the second column.
Two intervals t1 and t2 are said to be overlapping if and only if t2.start <= t1.end
Even if t1 entirely engulfs t2 , it's said to be overlapping.

Example 1

Input: [[1,5], [2,3], [4,8], [9,10]]
Output: [[1,8], [9,10]]

Example 2

Input: [[1,4], [5,8], [8,10], [12,15]]
Output: [[1,4], [5,10], [12,15]]

Example 3

Input: [[3,8], [4,6], [6,10]]
Output: [[3,10]]

Solutions

Brute Force Approach: Compare each interval with every other node in the list for overlapping.
Using Connected Components: Create a graph whose nodes are connected with other interval overlapping nodes.
Using Sorting of Intervals: Sort intervals on the basis of start value, then each overlapping intervals will be arranged sequentially.

You may try this problem here: Merge overlapping intervals

Learning via problem-solving is the best way to crack any interview!

1. Brute Force Approach

A simple approach is to start from the first interval and compare it with all other intervals for overlapping, if it overlaps with any other interval, then remove the other interval from the list and merge the other into the first interval.

Solution steps

Create a boolean array bMerge[] o f the size of the input intervals array and initialize with False.
For each pair of intervals(i, j) , check if it satisfies the above conditions to merge. If that so then set the bMerge[i] to True and update

intervals[j][0] with the minimum value of intervals[i][0] and intervals[j][0]
intervals[j][1] with the maximum value of intervals[i][1] and intervals[j][1]

3. For each False value of bMerge[i] , push intervals[i] to the result array.

Pseudo Code

// Driver function
int[][] mergeIntervals(int[][] intervals) { 
    int[][] result
    bool[] bMerge
    for (int i = 0 to i < intervals.size()-1) {
        for (int j = i+1 to j < intervals.size()) {
            bMerge[i] = bMerge[i] or merge(intervals[i], intervals[j])
        }
    }
    for (int i = 0 to i < intervals.size()) {
        if (bMerge[i] is false) {
            result.add(intervals[i])
        }
    }
    return result
}
// Utility function
bool merge(int A[], int B[]) {
    if (A[1] < B[0] or B[1] < A[0]) {
        return false
    }
    B[0] = min(A[0], B[0])
    B[1] = max(A[1], B[1])
    return true
}

Complexity Analysis

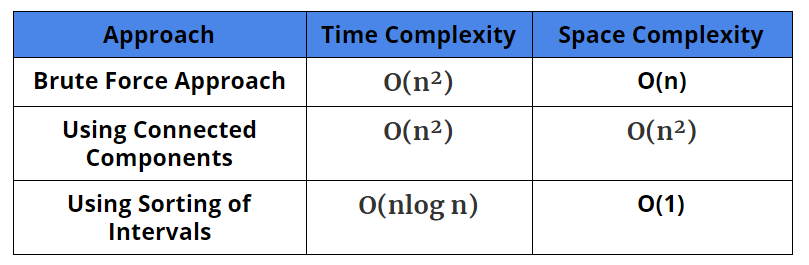
Time Complexity: O(n²)

Space Complexity: O(n)

Critical Ideas to Think

How is the merging of intervals done here?
Why does the utility merge function is updating the value of intervals[j] ?
Can you dry run this code using your own sample test case?

2. Using Connected Components

If we draw a graph (with intervals as nodes) that contains undirected edges between all pairs of intervals that overlap, then all intervals in each connected component of the graph can be merged into a single interval.

Here, we can represent the graph using adjacency list where the edges would be undirected. To determine which connected component each node is it, we perform graph traversals from arbitrary unvisited nodes until all nodes have been visited. To do this efficiently, we store visited nodes in a Set , allowing for constant time containment checks and insertion.

Now, you may consider each connected component, merging all of its intervals by constructing a new Interval with start equal to the minimum start among them and end equal to the maximum end.

If you will think, then you will realize that this algorithm is behaving like the brute force approach with the only difference that we gathered those nodes together. The reason for the connected component search is that two intervals may not directly overlap, but might overlap indirectly via a third interval.

Solution steps

To create a graph of type adjacency list use HashMap.
Now, get the connected components of the interval overlap graph.
use a depth-first search to mark all nodes in the same connected component with the same integer.
For each component, merge all intervals into one interval.

Pseudo Code

// global variables
map(int[], int[][]) graph
map(int, int[]) nodesInComp
set(int) visited
// Utility functions
bool overlap(int[] a, int[] b) {
    return a[0] <= b[1] && b[0] <= a[1]
}
// build a graph where an undirected edge between intervals u and v exists
// if u and v overlap.
void buildGraph(int[][] intervals) {
    for (int[] interval : intervals) {
        graph.put(interval, new [])
    }
    
    for (int[] interval1 in intervals) {
        for (int[] interval2 in intervals) {
            if (overlap(interval1, interval2)) {
                graph.get(interval1).add(interval2)
                graph.get(interval2).add(interval1)
            }
        }
    }
}
int[] mergeNodes(int[][] nodes) {
    int minStart = nodes.get(0)[0]
    for (int[] node in nodes) {
        minStart = min(minStart, node[0])
    }
   int maxEnd = nodes[0][1]
    for (int[] node in nodes) {
        maxEnd = max(maxEnd, node[1])
    }
    return new int[] {minStart, maxEnd};
}
void markComponentDFS(int[] start, int compNumber) {
    Stack(int[]) stack
    stack.add(start)
    while (stack is not Empty) {
        int[] node = stack.pop()
        if (not visited.contains(node)) {
            visited.add(node)
            if (nodesInComp[compNumber] is null) {
               nodesInComp[compNumber] = new []
            }
            nodesInComp[compNumber].append(node)
            for (int[] child in graph[node]) {
                stack.push(child)
            }
        }
    }
}
// gets the connected components of the interval overlap graph.
void buildComponents(int[][] intervals) {
    int compNumber = 0
    for (int[] interval in intervals) {
        if (!visited.contains(interval)) {
            markComponentDFS(interval, compNumber)
            compNumber = compNumber + 1
        }
    }
}
// Driver Function
int[][] mergeIntervals(int[][] intervals) {
    buildGraph(intervals)
    buildComponents(intervals)
    int[] merged
    for (int comp = 0 to comp < nodesInComp.size()) {
        merged.add(mergeNodes(nodesInComp[comp]))
    }
    return merged
}

Complexity Analysis

Time Complexity: O(n²). Building the graph costs O ( V + E )= O ( V )+ O ( E )= O ( n )+ O ( n² )= O ( n² ) time, as in the worst case all intervals are mutually overlapping.

Space Complexity: O(n²). In the worst case, there will be an edge for every pair of intervals.

Critical Ideas To Think

Why did we use the adjacency list instead of the adjacency matrix?
How did we check that an interval belongs to which component and how did markComponentDFS() help to achieve it?
Can you dry-run this pseudo-code on the above sample test cases?
Can you think of a more optimized approach?

3. Using Sorting of Intervals

Till now you would have realized that if we can arrange the intervals in any fashion such that their start time would be together, then we could say that each set of intervals that can be merged will appear as a continuous run.

So, we will sort the intervals on the basis of start value in ascending order. The possible conditions to verify the merging of intervals could be — If the current interval begins after the previous interval ends, then they do not overlap and we can append the current interval to merged . Otherwise, they do overlap, and we merge them by updating the end of the previous interval if it is less than the end of the current interval.

Solution steps

Sort the intervals on the basis of start value in ascending order
Create a merged array
If the list of merged intervals is empty or if the current interval does not overlap with the previous, simply append it.
Otherwise, there is overlap, so we merge the current and previous intervals.

Pseudo Code

int[][] mergeIntervals(int[][] intervals) {
    intervals.sort( key = intervals[0] )
    // to store merged resultant intervals
    int[][2] merged
    for( int i=0 to i < intervals.size()){
        if ( not merged or merged[merged.size()-1][1] < intervals[i][0]){
            merged.add(intervals[i])
        } else {
            merged[merged.size()-1][1] = max(merged[merged.size()-1][1], intervals[i][1])
        }
    }
    return merged
}

Complexity Analysis

Time Complexity: O(n log n)

Space Complexity: O(1). If the sorting is in place.

Critical Ideas to Think

How does sorting help in merging the intervals?
Do you think that sorting the intervals on the basis of end value in descending order will help to solve the problem? If not, Why?
How are we merging the intervals?