Lowest Common Ancestor of a Binary Tree

Lowest Common Ancestor of Binary Tree

Difficulty: Medium

Asked in: Amazon, Facebook, Adobe

Understanding The Problem

Problem Description

Given a binary tree, write a program to find the lowest common ancestor (LCA) of two given nodes in the tree.

Problem Note

Lowest Common ancestor: The lowest common ancestor is defined between two nodes node1 and node2 as the lowest node in a tree that has both node1 and node2 as descendants (a node can be a descendant of itself).
All of the node’s values will be unique.
node1 and node2 are different and both values will exist in the binary tree.
You can use extra memory, helper functions, and can modify the node struct but, you can’t add a parent pointer.

Example 1

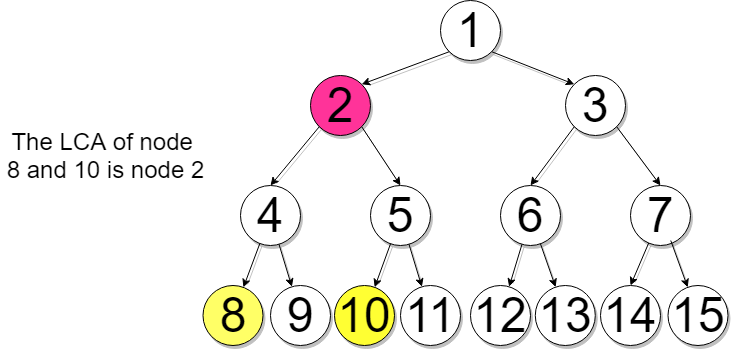
Example 2

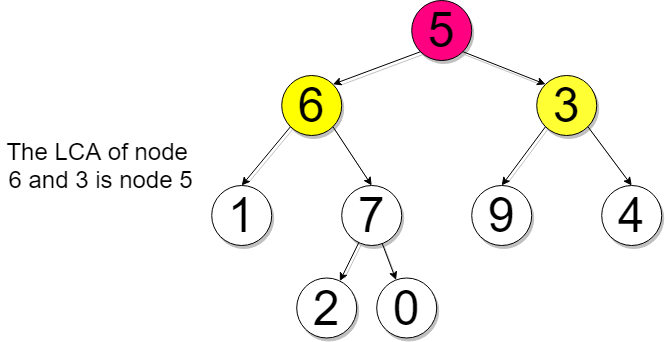
The node structure passed to your function will be

class TreeNode
{
    int data
    TreeNode left
    TreeNode right
}

Solutions

We will be discussing recursive and iterative approaches

Recursive approach — Recursively look for any of the two nodes and return it, the first node to encounter both of them in its subtree is the ancestor.
Iterative approach — Follow the recursive procedure by using a stack and a parent map for each node.

1. Recursive Approach

A pretty intuitive approach is to traverse the tree in a depth-first manner. The moment you encounter either of the nodes node1 or node2 , return the node. The least common ancestor would then be the node for which both the subtree recursions return a non-NULL node. It can also be the node which itself is one of node1 or node2 and for which one of the subtree recursions returns that particular node.

Solution steps

Start traversing the tree from the root node.
If the current node itself is one of node1 or node2 , we would return that node.
If the left or the right subtree returns a non-NULL node, this means one of the two nodes was found below.
If at any point in the traversal, both the left and right subtree return some node, this means we have found the lowest common ancestor for the nodes node1 and node2 .

Pseudo Code

TreeNode lowestCommonAncestor(TreeNode root, TreeNode node1, TreeNode node2) {
    if(not root)
        return NULL
    if (root == node1 or root == node2) 
        return root
    TreeNode left = lowestCommonAncestor(root.left, node1, node2)
    TreeNode right = lowestCommonAncestor(root.right, node1, node2)
    if(not left)
        return right
    else if(not right)
        return left
    else
        return root
}

Complexity Analysis

Time Complexity : O(n), where n is the total number of nodes in the tree.

Space Complexity : O(n)

Critical ideas to think

How will this algorithm work if the lowest common ancestor of node2 is an ancestor of node1?
Can you think of a case when the worst-case space complexity is O(n)?
How does this algorithm work if any of the two nodes fail to exist in the tree?

2. Iterative Approach

An intuition for an iterative approach is if we have parent pointers for each node we can traverse back from node1 and node2 to get their ancestors. The first common node we get during this traversal would be the LCA node. So, We can save the parent pointers in a dictionary as we traverse the tree.

Solution step

Start from the root node and traverse the tree.
Until we find node1 and node2 both, keep storing the parent pointers in a dictionary.
Once we have found both node1 and node2 , we get all the ancestors for node1 using the parent dictionary and add to a set called ancestors .
Similarly, we traverse through ancestors for node node2 . If the ancestor is present in the ancestors set for node1 , this means this is the first ancestor common between node1 and node2 (while traversing upwards) and hence this is the LCA node.

Pseudo Code

TreeNode lowestCommonAncestor(TreeNode root, TreeNode node1, TreeNode node2) {
    // create a parent map that maps the childnode with its parent
    map parent({{root,NULL}})
    // a stack to make a post order traversal iteratively 
    stack stk({root})
    while(not node1 exist in parent or not node2 exist in parent){
        TreeNode n = stk.top()
        stk.pop()
        if(n.left) {
            parent[n.left] = n
            stk.push(n.left)
        }
        if(n.right) {
            parent[n.right] = n
            stk.push(n.right)
        }
    }
    // ancestor set for node1
    set path
    while(node1 is not NULL) {
        path.insert(node1)
        node1 = parent[node1]
    }
    // The first ancestor of node2 which appears in
    // node1's ancestor set is their lowest common ancestor.
    while(node2 not exist in path) 
        node2 = parent[node2]
    return node2
}

Complexity Analysis

Time Complexity: O(n)

Space complexity : O(n). In the worst-case space utilized by the stack, the parent pointer dictionary and the ancestor set would be n each, since the height of a skewed binary tree, could be n .

Critical Ideas to Think

Which traversal technique we are using for traversal in the tree for this algorithm?
Why did we maintain a hash map?
What if one of the nodes is itself the LCA?
What exactly does the path set represents in the pseudo code?
Can you think of an iterative approach without using hashmap or storing parent pointer?