Knight on chessboard
AfterAcademy Tech
•
07 Sep 2020

Difficulty: Hard
Asked in: Amazon, Goldman Sachs
Understanding The Problem
Problem Description
Given a square chessboard of A x B size, the position of Knight (C, D) and the position of a target (E, F) is given. Write a program to find out the minimum steps a Knight will take to reach the target position.
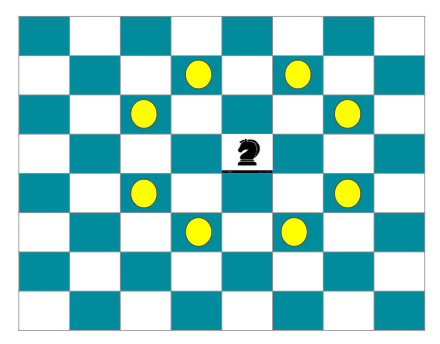
- The above figure describes the movements for a knight (8 possibilities).
- If the knight can not move from the source point to the destination point, then return
-1. - A knight cannot go out of the board.
Input Format
Following is the description of the parameters of the function “knight()”:
int A and int B: denotes the size of the chessboard
int C and int D: denotes the position of the Knight
int E and int F: denotes the target of the Knight
Example
Input: A = 6, B = 6, C = 1, D = 1, E = 4, F = 5
Output: 3
Explanation: The size of the chessboard is 6x6, the knight is initially at (1, 1) and the knight wants to reach position (4, 5).
The minimum number of moves required for this is 3. (1,1)->(3,2)->(5,3)->(4,5)
Solution
This problem can be solved by BFS(Breadth-First Search) algorithm.
If you have played chess then you know that a knight moves two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L).
The problem asked us to find the least number of moves to move the knight from position [C,D] to position [E,F] . Let’s imagine the chessboard as a graph where each square of the chessboard[x,y] is a vertex and the edges can be one legal move of the knight. The below image is showing how it will look if you consider the chessboard as a graph.
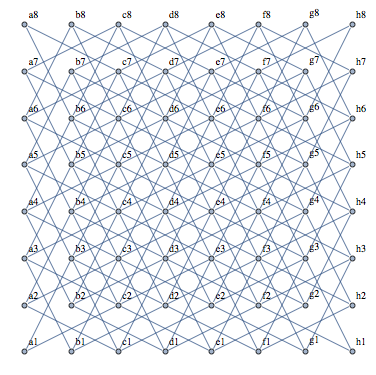
Now, we have considered it as a graph, we can use the BFS algorithm to find the shortest path from square [C,D] to square [E,F] .
So, starting from the initial position we will try to make all 8 legal moves. If the reachable position is not already visited and is inside the board, we enqueue this state into a queue with a number of moves of 1 more than its parent state. If the current location is not the target location, then we can pop it from the queue and will enqueue the possible legal moves from that location.
Solutions Steps
- Create a boolean
visitedarray ofA x Bwhich will be initialized with False. - Create a
movesarray ofA x Bwhich will store the number of moves required to reach there from the initial position. - Create a queue and push the knight’s starting position in it.
- Mark the visited array corresponding to the knight’s location as True.
- Now do the following until the queue is empty or the knight reaches the target location.
- Pop from the queue and store it in variable
x. - If
xis the target location, returnmoves[x] - Visit all the possible locations from the location
xand increase the number of moves accordingly in themovesarray.
Pseudo Code
int minStepToReachTarget(int A, int B, int C, int D, int E, int F)
{
int dx[] = [ -2, -1, 1, 2, -2, -1, 1, 2 ]
int dy[] = [ -1, -2, -2, -1, 1, 2, 2, 1 ]
// queue for storing states of knight in board
Queue q
q.push([C, D])
bool visited[A + 1][B + 1] = {false}
visited[C][D] = true
int moves[A + 1][B + 1] = {0}
while (q is not empty) {
x = q.pop();
if (x[0] == E and x[1] == F)
return moves[x[0]][x[1]]
// loop for all reachable states
for (int i = 0; i < 8; i++) {
new_pos_x = x[0] + dx[i]
new_pos_y = x[1] + dy[i]
if (isInside(new_pos_x, new_pos_y, A, B) and !visited[new_pos_x][new_pos_y]) {
visit[new_pos_x][new_pos_y] = true
moves[new_pos_x][new_pos_y] = moves[x[0]][x[1]] + 1
q.push([new_pos_x][new_pos_y])
}
}
}
// If all possible locations visited and no target location found
return -1
}
// utility function
bool isInside(int x, int y, int A, int B) {
if (x >= 1 && x <= A && y >= 1 && y <= B)
return true
return false
}
Complexity Analysis
Time Complexity: O(A.B)
Space Complexity: O(A.B)
where A and B are the dimensions of the board.
Critical Ideas To Think
- Why did we create dx and dy arrays?
- Why does BFS is chosen over DFS here?
- Read about a knight's tour from here to understand how the chessboard is assumed to be a graph and how come a knight can move to any different square from here.
- Can you think of some other approach to solve this problem? Think dynamic programming approach!
Suggested Problems To Solve
- Count of all possible ways to reach a target by a Knight
- Minimum steps to reach a destination
- N queen problem
- Can a knight visit all the squares of the board
- Surrounded Regions
Please comment down below if you have a better insight in the above approach.
Happy Coding, Enjoy Algorithms!