Interleaving Strings

Interleaving String

Difficulty: Hard

Asked in: Google, Microsoft, Yahoo

Understanding The Problem

Problem Description

Given three strings S1 , S2 and S3 , write a program that checks whether S3 is an interleaving of S1 and S2 .

Problem Note:

S3 is said to be interleaving S1 and S2 if it contains all characters of S1 and S2 and the order of all characters in individual strings is preserved.

Example 1

Input: S1 = "xxyzz", S2 = "wyyzx" and S3 = "xxwyyzyzxz"
Output: true
Explanation:"xx" (from S1) + "wyyz" (from S2) + "yz" (from S1) + "x" (from S2) + "z" (from S1)

Example 2

Input: S1 = "xxyzz", S2 = "wyyzx", S3 = "xxwyyyxzzz"
Output: false
Explanation: It is not possible to get S3 by interleaving S1 and S2.

Solutions

Brute Force
Dynamic Programming

You may try this problem here.

1. Brute Force Approach

If you will look at the above examples, you will conclude that there are two possibilities that need to be taken care of :-

If the first character of S3 matches the first character of S1 , we move to the next character ahead in S1 and S3 and recursively call the function.
If the first character of S3 matches the first character of S2 , we move to the next character ahead in S2 and S3 and recursively call the function.

Solution Step

Check if S1 , S2, and S3 are empty, then return True. This will be the base case for our recursive function as empty S3 is interleaving of S1 and S2 .
Check if S3 is empty and either of S1 and S2 is not empty, then return False, which will mean len(S3) is smaller than len(S1) + len(S2) (How?)
Now if those are not the case, then move ahead with the two possibilities discussed above.

If S3[0] == S1[0] , then check for S1[1…], S2, S3[1...]
If S3[0] == S2[0] then check for S1, S2[1…], S3[1…]
If any of the above mentioned two possibilities is true, then return true, otherwise false

Pseudo Code

bool isInterleaved( char[] S1, char S2, char S3) { 
    // Base Case: If all strings are empty 
    if ( not (len(S1) != 0 or len(S2) != 0 or len(S3) != 0) )
        return true
    if (len(S3) == 0) 
        return false
    return ((S3[0] == S1[0]) and isInterleaved( S1 + 1, S2, S3 + 1))
      or ((S3[0] == S2[0]) and isInterleaved( S1, S2 + 1, S3 + 1))
}

Complexity Analysis

Time Complexity: O(2^n)
For every character of S3 , there can be 2 options so the time complexity is O(2^n).

Space Complexity: O(1), not considering recursion stack space.

Critical Ideas To Think

Can you explain, how did the base help in solving the problem?
What did we do, when the first character of S3 matches with both the first character of S1 and the first character of S2 ?

2. Dynamic Programming

The above recursive solution certainly has many overlapping sub-problems. For example, if we consider S1 = “AAA”, S2 = “AAA” and S3 = “AAAAAA” and draw recursion tree, there will be many overlapping subproblems. Therefore, the solution to this problem could be optimized using Dynamic Programming.

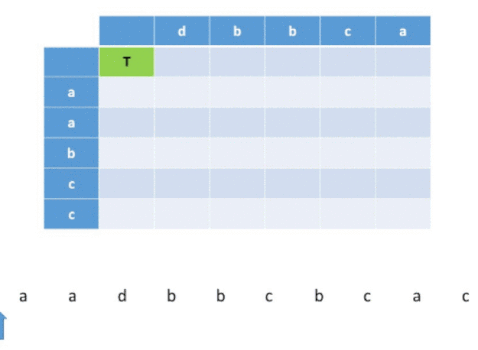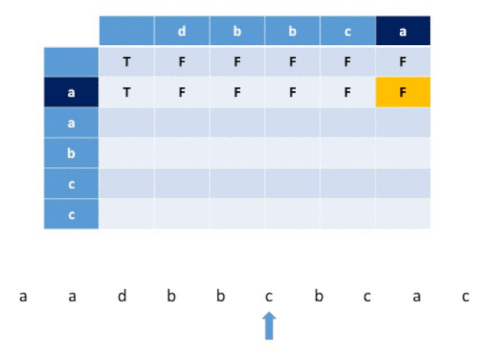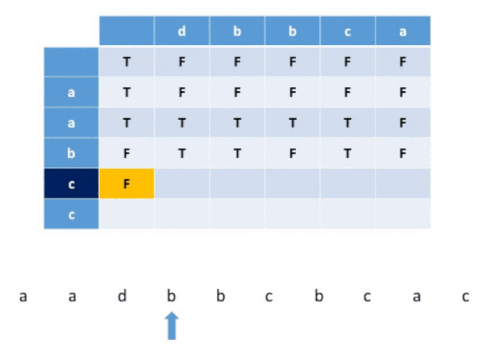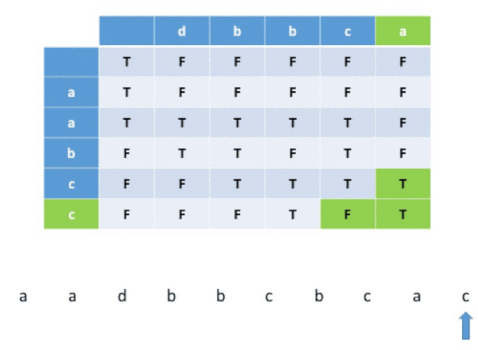
The idea is to build a two-dimensional DP table, according to the drawn path displayed below. Because it’s interleaving, so certain order still needs to be maintained, so that’s why for a valid path, it can only go right or down. That’s why DP[i][j] is depending on DP[i - 1][j] and DP[i][j - 1] .

After discovering the transition rule to get DP[i][j] , we just need to record true or false in the DP table. DP[i][j] means if s3.substr(0, i + j) can be formed by s1.substr(0, i) interleaving s2.substr(0, j) .

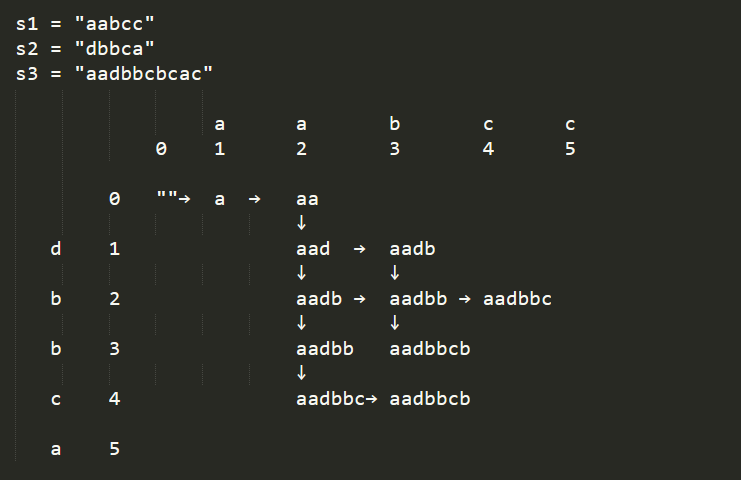
If you will look over the above example, you will understand how will DP table will help to build the solution.

To implement this method, we’ll make use of a 2D boolean DP array. In this array DP[i][j] implies if it is possible to obtain a substring of length (i+j+2) which is a prefix of S3 by some interleaving of prefixes of strings S1 and S2 having lengths (i+1) and (j+1) respectively.

In short, DP table represents if S3 is interleaving at (i+j)th index when S1 is at ith index, and S2 is at jth index. 0th index means an empty string.

So, if both S1 and S2 is currently empty, S3 is empty too, and it is considered interleaving. If only, S1 is empty, then if the previous S2 position is interleaving and the current S2 position character is equal to S3 current position character, it is considered interleaving. A similar idea applies when S2 is empty. when both S1 and S2 are not empty, then whenever we arrive i, j from i-1, j , and if i-1,j is already interleaving and i and current S3 position are equal, then they are interleaving. If we arrive i,j from i, j-1 , and if i, j-1 is already interleaving and j and current S3 position equal then also it is interleaving.

Visualization for a example

Solution Steps

Create a 2D boolean DP array of size m+1, n+1 . Where m and n are the lengths of S1 and S2
Now fill the DP table by comparing the characters of S1, S2 with S3 accordingly.
Return DP[m][n]

Pseudo Code

bool isInterleave(char[] S1, char[] S2, char[] S3) {
    if(S3.length() != S1.length() + S2.length())
        return false

    bool DP[S1.length()+1][S2.length()+1]
    
    for(int i=0 to i < s1.length()+1)
        for(int j=0 to j < s2.length()+1){
            if(i==0 and j==0)
                DP[i][j] = true
            else if(i == 0)
                DP[i][j] = ( DP[i][j-1] and S2[j-1] == S3[i+j-1])
            else if(j == 0)
                DP[i][j] = ( DP[i-1][j] and S1[i-1] == S3[i+j-1])
            else
                DP[i][j] = (DP[i-1][j] and S1[i-1] == S3[i+j-1] ) or 
                           (DP[i][j-1] and S2[j-1] == S3[i+j-1] )
        }
        
    return DP[S1.length()][S2.length()]
}

Complexity Analysis

Time complexity: O ( m ⋅ n )

Space complexity: O ( m ⋅ n ).

Where m and n are the lengths of S1 and S2 respectively.

Critical Ideas To Think

Can you prove that the transaction formula for this problem is dp[i][j] = (dp[i-1][j] & s3[i+j-1] == s1[i-1]) || (dp[i][j-1] & s2[j-1] == s3[i+j-1]) ?
Can you think of a BFS approach for this problem?
The two possibilities discussed in the recursion approach have been taken care of in this approach. How?
An approach is to just merge the two strings. A pointer into each string. If the present character in the interleaved string c equals one of the strings a or b, increase the pointer to that string and to c, if not then return false. Do this for every character in c. Complexity will be O(m+n). Do you think, this approach will work? If not then, can you find a failing test case for such an approach?