Implement Queue Using Stack-Interview Problem

Implement Queue Using Stack- Interview Problem

Difficulty: Medium

Asked in: Microsoft, Adobe, Amazon, Goldman Sachs, Flipkart

Understanding the Problem:

Queue and Stack are both different data structures with different properties and also different use cases. However, the given problem is asking to implement one data structure, i.e., Queue, with the help of the other (Stack). Let us first look at the features and characteristics of Stack and Queue and try to get an idea of how we can implement them with the help of each other.

Stack and Queue

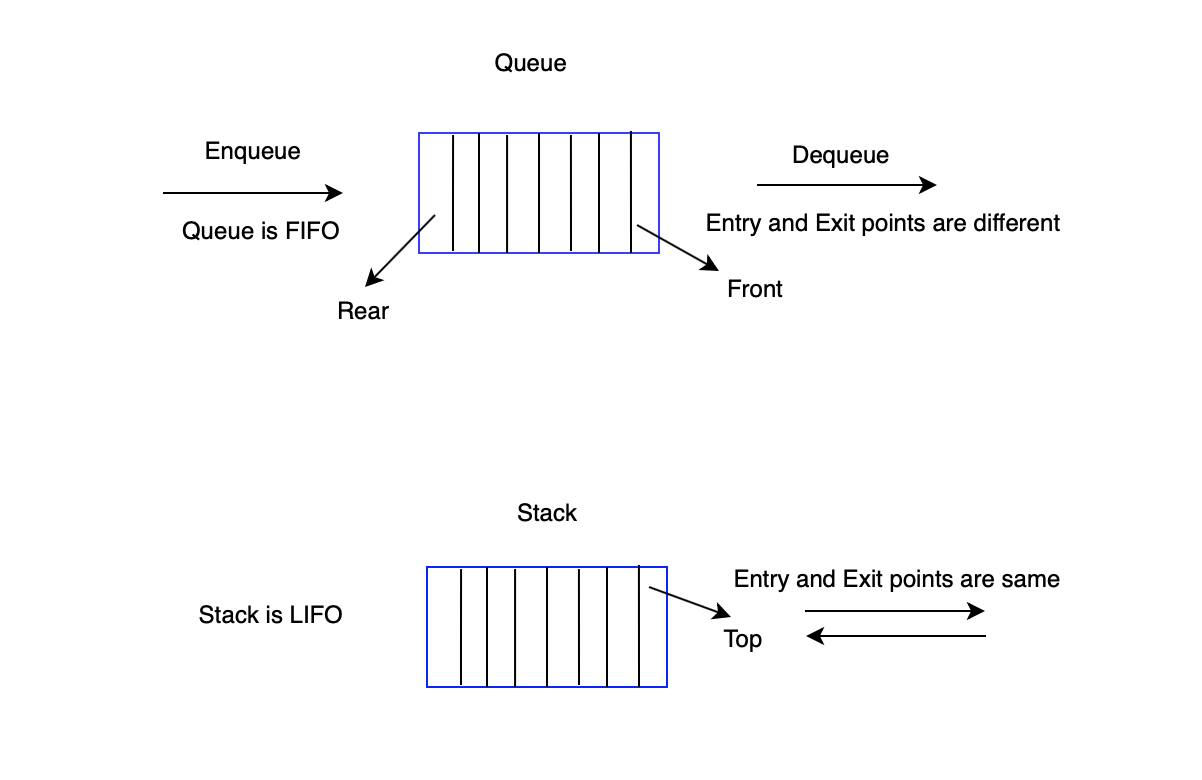
Stack is a LIFO based data structure and there is only one side in Stack(top) acting as entry and exit point in Stacks.
Stack supports operations like Push, Pop, Peek and isEmpty.
Queue is a FIFO based data structure and there are two different points, one for entry and the other one for exit.
Queue supports operations like enqueue, dequeue, peek and isEmpty.

Conclusion

We can implement Queue using two Stacks. Two Stacks taken together can help us to get all the operations as supported by Queue. All the use-cases of queue can be achieved by using two stacks. Try it yourself first!

Possible questions to ask the interviewer: →

Implementation of Queue using Stack can make one of the operation costly(enqueue or dequeue). Which operation needs to be less complex? ( Ans: You can choose either of the operation.)

Solutions

We are going to discuss two different approaches to this problem. Both the approaches, however, will require two stacks to be used. There is a third solution also, which is a little bit trickier, we will discuss it at the end with more details.

By making enqueue operation costly: We will try to insert in a way such that the first element inserted is at the top of the stack.
By making dequeue operation costly: In this, we try to optimize the enqueue operation but the dequeue operation becomes costly.

Modifying the Enqueue Operation

Solution idea

The idea here is to modify the insertion operation of the Queue so that it can be implemented using Stacks. Since in a queue the element which gets in first, gets out first so when using stack we have to figure out a way so that the element inserted first should present at the top of the stack. For this during insertion, we will use a second stack to push everything from the first stack into the second one and then push the element to be inserted into the first one then again all the elements from the second stack will be pushed to the first one. This way the insertion is costly but we can get a queue using stack.

Solution steps

Algorithm for Insertion

Take two stacks S1 and S2
If S1 is empty, insert directly into S1.
If S1 is not empty, push all the elements from S1 to S2.
Push the element to be inserted into S1.
Push everything from S2 back to S1.

Algorithm for Deletion

Pop-out the element from S1 if S1 is not empty.
If S1 is not empty, return -1.

Pseudo-code

class queueUsingStack
{
   stack <datatype> S1, S2

   void enQueue(int data)
   {
      while(S1 is not Empty)
      {
          int topElement = S1.top()
          S1.pop()
          S2.push(topElement)
      }

      S1.push(data)
      while(S2 is not empty)
      {
          int topElement = S2.top()
          S2.pop()
          S1.push(topElement)
      }
   }

   int deQueue()
   {
       if(S1 is empty)
          return -1   
       int topElement= S1.top()
       S1.pop()
       return topElement
   }

Complexity Analysis

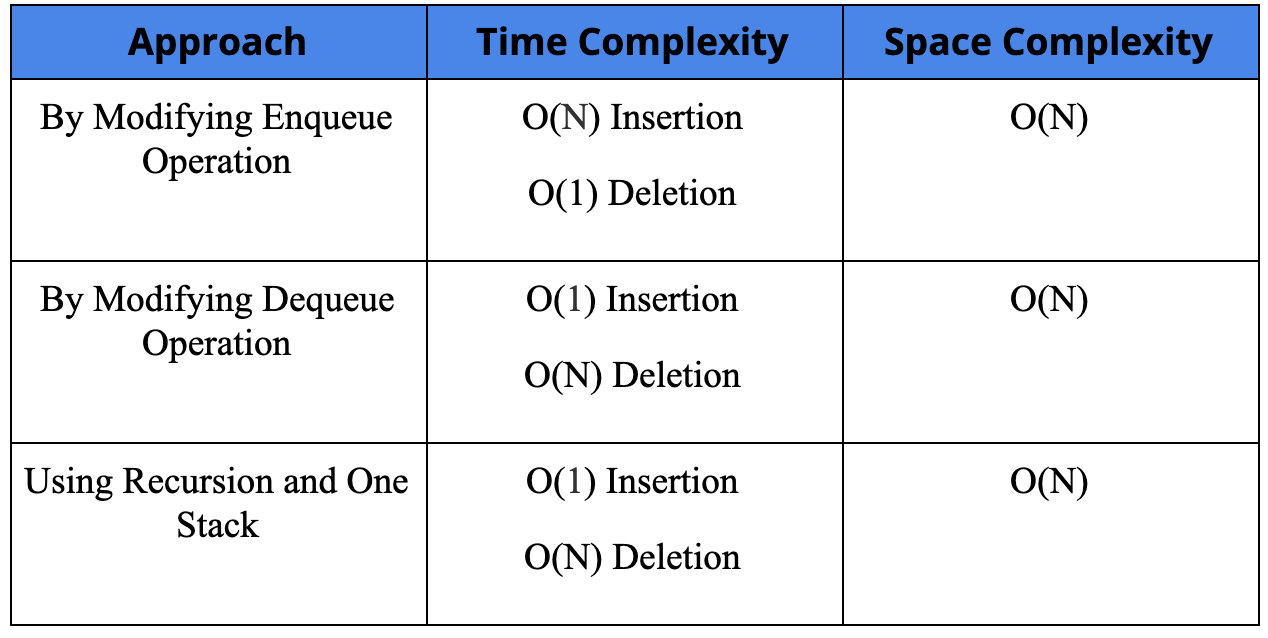
Time Complexity : O(N) for Insertion , O(1) for Deletion .

Space Complexity : O(N)

Critical ideas to think!

Which operation should we choose to make costly during queue implementation using stack? Is it dependent on the use-case?

Modifying the Dequeue Operation

Solution idea

Here we modifying the deletion or the dequeue operation of the queue. This will lead to the dequeue operation being more costly but it will help in implementing queue with stacks. For deleting we first need to check if both the stacks(as we are using two) are not empty and if this condition is true, we will simply move all the elements from stack S1 to stack S2. This will let the first element inserted into the stack to be at the top. We will then perform a pop operation on stack S2.

Solution steps

Algorithm for Insertion

Take two stacks S1 and S2.
Push everything to S1 taking into consideration that S1 has unlimited size.

Algorithm for Deletion

If both S1 and S2 is empty return -1.
Push everything to S2 from S1.
Delete(pop) the top element from S2.

Pseudo-code

class queueUsingStack
{
   stack <datatype> S1, S2
   void enQueue(int data)
   {
      S1.push(data)
   }
   int deQueue()
   {
      if( S1 is empty and S2 is empty)
         return -1
      while(S1 is not empty)
      { 
         int topElement = S1.top()
         S2.push(topElement)
         S1.pop()
      }
      int topElement = S2.top()
      S2.pop()
      return topElement
    }
}

Complexity Analysis

Time Complexity : O(N) for dequeue and O(1) for enqueue.

Space Complexity : O(N) (Why?)

Using Recursion Stack in place of Second Stack

Solution idea

The idea of this solution is very obvious but does not comes to mind very often. In the all above solutions, we are using two stacks, here in this solution we will use one stack and the other one is the recursion call stack. This idea can be used in both the above methods. We are going to discuss the implementation of the second method using this.

Solution steps

Algorithm for Insertion

We will take a stack S1 and will keep pushing the data into it considering it to be of unlimited size.

Algorithm for Deletion

Here we will make use of the recursion stack.
If the stack S1 is empty or has only one element(base condition), we can simply return -1 or that element.
If that is not the case we will take help of the recursive stack to reverse the given stack S1 so that we can get the last element of the stack at the top or while deleting.

Pseudo-code

class queueUsingStack
{
  stack <datatype> S1
  void enQueue(int data)
  {
     S1.push(data)
  }
  int deQueue()
  {
    if(S1 is empty)
     return -1
    int topElement = S1.top()
    S1.pop()
    if(S1 is empty)
     return topElement
    int result = deQueue()
    S1.push(topElement) //reversing the stack
    return result
   }
}