Find an Element In a Bitonic Array

Find an Element in Bitonic Array

Difficulty : Easy

Asked in: Amazon

Understanding the problem

Problem Description

Given a bitonic sequence of n distinct elements, write a program to search a given element k in the bitonic sequence.

Problem Note →

A Bitonic Sequence is a sequence of numbers that is first strictly increasing then after a point strictly decreasing.
It is guaranteed that there are no duplicates in the input array.
If the element is found then return the index otherwise return -1.
You are expected to solve this problem in O(log N) time complexity.

Example 1

Input: nums[] = [-3, 8, 9, 20, 17, 5, 1], k = 20
Output: 3 
Explanation: Element k Found at index 3

Example 2

Input: nums[] = [5, 6, 7, 8, 9, 10, 3, 2, 1], k = 30
Output: -1

Solutions

Linear Search — Scan each element from left to right.
Binary Search — Find peak element and then perform a binary search on one of the halves of the array.

1. Linear Search

In this approach, we make use of the fact that two consecutive numbers nums [ i ] and nums [ i +1] are never equal. Thus, we can traverse over the nums array from the beginning while comparing each element with the key. If the ith element is equal to the k value, then we will return the index of the element. If the element is not found, we will simply return -1.

Psudo Code

// size is the size of the nums array
int findBitonic(int[] nums, int size, int k) {
    for (i = 0 to i < size ) {
        if (nums[i] == k)
            return i
    }
    return -1
}

Complexity Analysis

Time complexity: O ( n ). We traverse the nums array of size n once only.
Space complexity: O (1). Constant extra space is used.

Critical Ideas to Think

Does the property of the bitonic array used in this approach?
Why does the time complexity in this approach is O(n)?

2. Binary Search

A more efficient way to solve this problem is by using a binary search as the input nums array is Bitonic, i.e strictly increasing and then after a certain point it is strictly decreasing, so we may find the peak element of the array by using binary search. The peak element of the bitonic array could divide the array into two parts, the first part would be increasing array and the second part would be decreasing array. Then we could easily perform binary search on any of the sub-part of the nums array depending on the peak value and the value k .

Example —

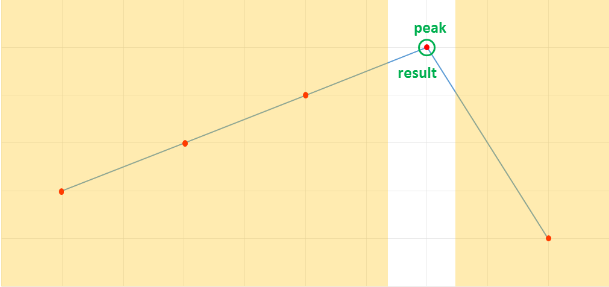
In the above figure, the peak element divides the array into two parts. Now, you can separately apply binary search on the increasing subarray and decreasing subarray and return the index of the element if found. Otherwise, just return -1.

But we first need to find the peak element using binary search →

We start off by finding the middle element, mid from the given nums array. If this element happens to be lying in a descending sequence of numbers or a local falling slope(found by comparing nums [ i ] to its right neighbor), it means that the peak will always lie towards the left of this element. Thus, we reduce the search space to the left of mid (including itself) and perform the same process on the left subarray.
If the middle element, mid lies in an ascending sequence of numbers, or a rising slope(found by comparing nums [ i ] to its right neighbor), it obviously implies that the peak lies towards the right of this element. Thus, we reduce the search space to the right of mid and perform the same process on the right subarray.
In this way, we keep on reducing the search space until we eventually reach a state where only one element is remaining in the search space. This single element is the peak element.

In short,

If mid element is greater than both of its adjacent elements, then mid is the peak element. Example — [1, 3, 5, 7, 6, 4, 2]
If mid element is greater than its next element and smaller than the previous element then maximum lies on the left side of mid. Example — [1, 7, 6, 5, 4, 3]
If mid element is smaller than its next element and greater than the previous element then maximum lies on the right side of mid. Example — [2, 4, 5, 6, 7, 3, 1]

Solution steps

Find the peak point of the bitonic array
If the element to be searched is equal to the peak element then return its index.
If the element to be searched is greater than the element at peak point then the element does not exist in the array.
If the element to be searched is less than the element at peak point then search for that element in both halves of the array using binary search.

Pseudo Code

int findPeakElement(int[] nums, int low, int high) {
    if (low == high)
        return low
    mid = (low + high) / 2
    if (nums[mid] > nums[mid + 1])
        return findPeakElement(nums, low, mid)
    return findPeakElement(nums, mid + 1, high)
}

// Function for binary search in ascending part of array 
int ascendingBinarySearch(int arr[], int low, int high, int key) {
    while (low <= high) {
        mid = low + (high - low) / 2
        if (arr[mid] == key)
            return mid
        if (arr[mid] > key)
            high = mid - 1
        else
            low = mid + 1
    }
    return -1
}

// Function for binary search in descending part of array
int descendingBinarySearch(int arr[], int low, int high, int key) {
    while (low <= high) {
        mid = low + (high - low) / 2 
        if (arr[mid] == key)
            return mid 
        if (arr[mid] < key)
            high = mid - 1 
        else 
            low = mid + 1 
    }
    return -1 
}

// driver function
int findBitonic(int[] nums, int size, int k) {
    peak_index = findPeakElement(nums, 0, size-1)
    if(k > nums[peak_index]) 
        return -1
    else if(key == nums[peak_index]) 
        return peak_index 
    else {
        temp = ascendingBinarySearch(nums, 0, peak_index-1, k) 
        if (temp != -1) { 
            return temp 
        }
        // Search in right of k 
        temp = descendingBinarySearch(nums, peak_index+1, size-1, k)
        if(temp != -1){
            return temp
        }
    }
    return -1
}

Complexity Analysis

Time complexity : O ( log ( n )). We reduce the search space in half at every step.
Space complexity : O ( log ( n )). We reduce the search space in half at every step. Thus, the total search space will be consumed in log ( n ) steps. Thus, the depth of the recursion tree will go up to log ( n ).

We can reduce the space complexity from O(log n) to O(1) by using an iterative function for finding the peak element instead of a recursive function.

// Pseudo-code for finding the peak element in the bitonic array
int findPeakElement(int[] nums, low, high) {
    while (low < high) {
        mid = (low + high) / 2
        if (nums[mid] > nums[mid + 1])
            high = mid
        else
            low = mid + 1
    }
    return low
}

Critical Ideas to Think

Why did we find the peak element first in the above approach?
Comparing nums[mid] with nums[mid+1] helps in finding the peak element. How?
Can you convert ascending and descending binary search functions to recursive?